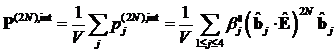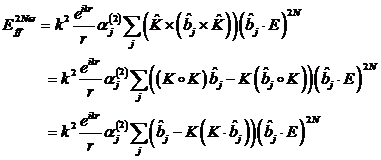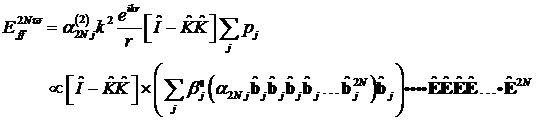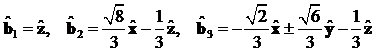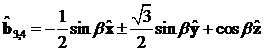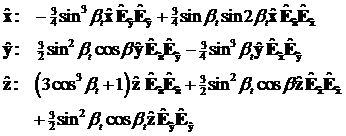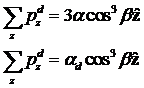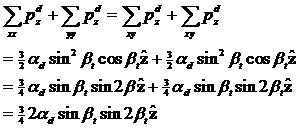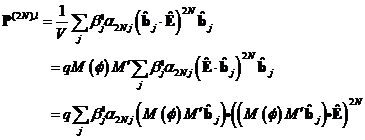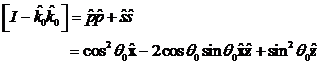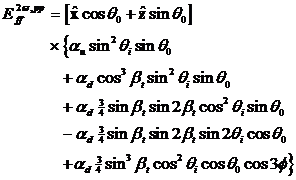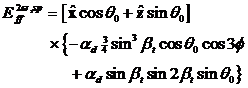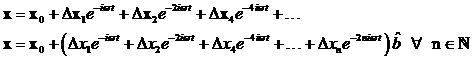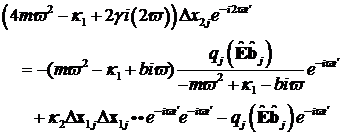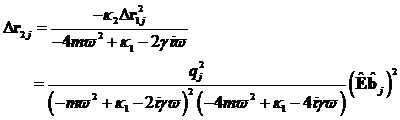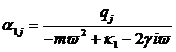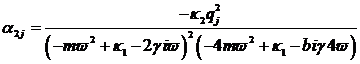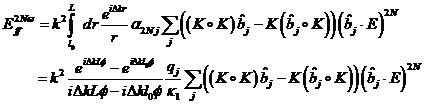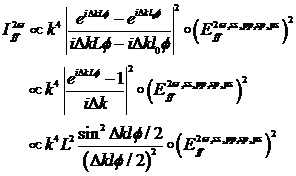| Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie |
          |
Kapitel
6
SBHM- Modell: Kollektives Verhalten
NZS gebundener Elektronen
6.1
Einführung
In diesem Abschnitt wird das
kollektive Verhalten der Oberflächenelektronen anhand des Si- SiO2
Materialsystems untersucht. SHG und Hohe Harmonische im Si- SiO2
Materialsystem kann an einer Schnittstellenregion, welche nur wenige Atomlagen
dick ist, erzeugt werden, da dort aufgrund asymmetrisch angeordneter Bindungselektronen
die Inversionssymmetrie gestört ist und sich so vom Bulk unterscheiden. Aus
diesem Grund basiert der mathematische Formalismus für SHG und hohe Harmonische
für NZS- Materie auf den Eigenschaften jedes einzelnen Bindungselektrons im
asymmetrischen Potential. Die Generation von SHG und hohen Harmonischen kann
vorteilhaft durch das vereinfachte Bindungs- Hyperpolarisations- Modell, engl. Simplified bond- hyperpolarizability model (SBHM) beschrieben werden. Der
signifikante Vorteil dieses Modells liegt darin, dass die ganze NLO-Theorie auf
Atomniveau formuliert wird, welche die Responses aus den Termen der Bindungs-
Hyperpolarisationen und der Kristallsymmetrien unter Einbeziehung der
anisotropen Responses der Bindungsladung ergeben. Es werden die ursprünglichen
vereinfachenden Annahmen von Powell et al für das SBHM zugrunde gelegt, welche
hinreichend genau sind um SFG beschreiben zu können. Dabei ist für eine gegebene
Bindung anzunehmen, dass die dazugehörige Ladungsbewegung entlang der
Bindungsrichtung ist, welches die Annahme impliziert, dass die Bindungen
rotationssymmetrisch sind.
6.2
SHG Response für (111)- Si- SiO2
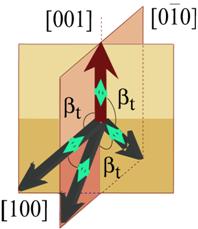
Für die spezielle Geometrie von singulären
(111) Oberflächen gibt es zwei Klassen von Schnittstellenbindungen: Eine
Bindung senkrecht zur Schnittstellenebene, und drei gleichwertige Bindungen
zwischen den Atomen der Schnittstellenebene und der Atomebene darunter, wie in
Abb. 6‑1 links gezeigt wird.
Für vicinale Oberflächen, wird sich eine der drei
hinteren (down) Bindungen nicht mehr gleichwertig zu den beiden anderen
Bindungen verhalten. Wenn der vicinale Schnitt von 5°
gegen die 
Richtung geht,
wird eine der "back" Bindungen eine "step"
Bindung, d. h. diese Bindung liegt in der Schnittebene. In diesem Fall wird der
vertikalen "up" Bindung eine komplexe
Hyperpolarisation 
zugewiesen und
den drei gleichwertigen hinteren Bindungen eine Hyperpolarisation
.
|
|
|
Abbildung 6‑1 zeigt
die tetraedrische Elektronenstruktur von (111) Si- SiO2- Oberflächen,
welche gewöhnlich eine "up" Bindung und
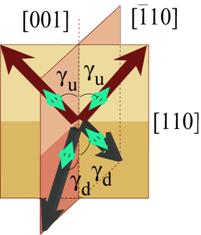
drei "back" Bindungen aufweisen (links). Zum Vergleich ist die
räumliche Anordnung der Elektronenstruktur für (001)- Oberflächen gezeigt
(Rechts). Die beiden "upper" Bindungen
befinden sich in der xz- Ebene mit den
Bindungswinkeln γu
und die beiden "down" Bindungen sind in der yz-
Ebene orientiert mit den Bindungswinkeln γd.
Dabei wurde die Konvention benutzt, in der alle Bindungen vom Zentral-Atom
wegzeigen und in die äußerste Ebene gerichtet sind.
Die Bindungsanordnungen an den
Schnittstellen selbst sind die gleichen, wie jene des Bulkmaterials und das
abgestrahlte Feld ergibt sich aus der kohärenten Überlagerung der Strahlung von
jeder Bindung, welche im Rahmen der Dipolmomentnäherung berechnet wurde.
Der Modellansatz des SBHM und die
Hauptresultate für nichtzentrosymmetrische Materie können wie folgt
zusammengefasst werden. In den Bindungen werden die Hyperpolarisationen
erzeugt, die von der Art der Bindung (up, back, step) abhängig sind. Die Dipolkomponenten gerader Ordnung 
sind entsprechend
gekoppelt mit den longitudinalen Hyperpolarisationen der Elektronen der j- ten Bindung im anharmonischen
Potential. Diese Dipolkomponenten können für NZS Systeme geschrieben werden
mit:
|
|
(6.1) |
Die einzelnen Dipolmomente 
jeder
beteiligten Bindung j des n- ten tetraedrisch koordinierten
Silizium- Zentralatoms mit 
, können
zum Gesamtbeitrag der Oberfläche aufsummiert werden. Damit erhält man das
Dipolmoment, welcher für den diskreten und kontinuierlichen Fall als Mittelung
über die Eigenschaften einer Einheitszelle formuliert werden kann:
|
|
(6.2) |
mit 
als paralleler
Beitrag der Hyperpolarisation. Die beobachtbaren Intensitäten 
im Fernfeld,
d. h. weit von der Probe entfernt, sind proportional zum Betragsquadrat
der Felder 
, welche
die Summen der kohärenten Strahlungsfelder sind, die durch die verschiedenen
Bindungen induziert werden. Diese Felder können für nichtzentrosymmetrische
Makromoleküle beschrieben werden mit:
|
|
(6.3) |
Um das System auf messbare Größen
zurückzuführen, können wir mit der Polarisationsdichte argumentieren und
erhalten für Makromoleküle:
|
|
(6.4) |
mit 
als
Einheitstensor (2N+1)- ter Stufe und 
als
Einheitswellenvektor in Richtung der bj,
welcher der Beziehung 
genügt.
Insgesamt ist 
der
Projektionsoperator der emittierten Strahlung, mit 
und 
als
Einheitsvektoren parallel zu den Strahlungsfeldern entsprechend ihrer
jeweiligen 
Polarisationen.
Diese Gleichungen haben die Form von externen Projektionsoperatoren, welche auf
die Produkte von bj wirkt. Diese
Operationen stellen ein Rezept bereit um eine Untergruppe von kompletten Sätzen
von Funktionen (xxx, xxy etc.
für SHG) zu generieren, die konsistent sind mit der Symmetrie der Schnittstelle.
Die späteren Berechnungen gestalten sich vorteilhaft, wenn eine der Bindungen
und die z-Achse normal zur Schnittstelle orientiert sind und eine der drei
gleichwertigen Bindungen in der xz-Ebene liegt.
In diesem Fall erhalten wir für
die "up", "step"
und den zwei gleichwertigen "down" Bindungen für jedes
vierfach-koordinierte Schnittstellenatom in kartesischen Koordinaten:
|
|
(6.5) |
Für die Analytische Form der HHG
Intensitäten für singuläre (111) Schnittstellen sind die Bindungswinkel zu
berücksichtigen. Die Bindungen bj von (111)
Schnittstellen in Kristallographischen Koordinaten lauten:
up Bindung:
|
|
(6.6) |
step Bindung:
|
|
(6.7) |
back
Bindungen:
|
|
(6.8) |
wobei eine der "back" Bindungen
in die xz-Ebene gedreht wurde, die der Koordinatentransformation
bezüglich der kartesischen Koordinaten mit 
und bezüglich
der Bindungswinkel- Koordinaten mit 
genügt. Dies bewirkt eine Transformation der
y- Koordinate, die in der Mitte der Verbindungslinie zu liegen kommt, mit 
. Der Bindungswinkel β entspricht dem Tetraederwinkel mit βt
= 109°. Die Wellenvektoren 
und 
beschreiben das einfallende Feld und das zu
beobachtende emittierte Feld relativ zu den Laborkoordinaten. Das einfallende
und das beobachtbare Feld in den Laborkoordinaten vorliegend, stehen senkrecht aufeinander
und können mit s- (TE-) und p- (TM-) polarisierten Moden beschrieben werden.
Die zu berücksichtigenden Komponenten sind für s- polarisiertes Licht 
und 
und für p- polarisiertes Licht 
und 
. Der Projektionsoperator belässt die s- Komponenten
unverändert, währenddessen die p- polarisierten Komponenten die Linearkombination
konstruieren. Die s- und p- polarisierten
Moden führen zu den jeweiligen Beobachtungs- Kombinationen, die konventionell
mit p-p, p-s, s-p und s-s bezeichnet werden, wobei sich der erste Buchstabe auf
die Polarisationen der einfallenden und der zweite Buchstabe auf die Polarisationen
der emittierten Strahlung bezieht.
6.3
Bindungselektronen in kristallographischen
Koordinaten
Die Berechnung erfolgt über triadische Produkte in Richtung der beteiligten Bindungen,
d. h. den Bindungsvektoren, in der zugrunde gelegten kartesischen Basis mit den
Basisvektoren e1, e2, e3
wird ein Tensorprodukt zugeordnet, der Form 
mit 
. Unter Berücksichtigung ihrer Symmetrieeigenschaften und
den heraus mittelnden ungeraden Projektionen, findet man für die Summierung
über alle Bindungselektronen die einzelnen Polarisations- Komponenten zu:
|
|
(6.9) |
Damit können wir auf die individuellen
Bindungsbeiträge schließen und erhalten:
„up“-
Bindung:
|
|
(6.10) |
„down“- Bindungen:
|
|
(6.11) |
|
|
(6.12) |
|
|
(6.13) |
Zur Berechnung der Quadrupolbeiträge
die von der Oberfläche generiert werden, muss die Kristallrotation berücksichtigt
werden. Den allgemeinen longitudinalen Beitrag für nichtzentrosymmetrische
Materie erhalten wir über die makroskopische Polarisation, welche die
Bindungstransformation für jede Bindung bj
enthält:
|
|
(6.14) |
mit 
als Matrix,
welche die Kristallrotation beschreibt und 
als Rotationsmatrix
um den Azimuthwinkel. Der Projektionsoperator ist an
der Grenzfläche stetig und erhalten mit 
für die Projektionen des einfallenden und
emittierten Strahles in der Polarisationskombination pp folgenden Satz von
Gleichungen:
|
|
(6.15) |
|
|
(6.16) |
Das einfallende und emittierte Feld
der „up“- Bindung genügt folgendem Satz von
Gleichungen:
|
|
(6.17) |
|
|
(6.18) |
|
|
(6.19) |
|
|
(6.20) |
Für die Einfalls- und Emissionspolarisation
erhalten wir insgesamt für die verschiedenen Bindungstypen:
„up“-
Bindung:
|
|
(6.21) |
„down“- Bindungen:
|
|
(6.22) |
|
|
(6.23) |
|
|
(6.24) |
|
|
(6.25) |
In dieser Modellbildung lassen sich
die von der Oberfläche generierten Felder für alle vier Polarisations- Kombinationen
pp, ps, sp und ss aufschreiben:
pp- Polarisation:
|
|
(6.26) |
ps- Polarisation:
|
|
(6.27) |
sp- Polarisation:
|
|
(6.28) |
ss- Polarisation:
|
|
(6.29) |
6.4
Spektral- Darstellung des SBHM
In diesem Abschnitt wird die
Gültigkeit des Modells durch Anwendung der experimentellen SHG Daten von Lübke et
al. [LBD94] für oxidierte vicinale (111) Si- Wafer
beurteilt. Wie man sehen konnte, kann im Resonanzfall das Bindungselektron im anharmonischen Potential nicht mehr als reine komplexe Lorentzkurve zu einer bestimmten Energie E beschrieben
werden. Deshalb wird die Multiresonanzform berechnet um höhere
Energieresonanzen zu approximieren und wird auf SHG angewendet. Ein angelegtes
optisches Feld bewirkt mit den gewählten Randbedingungen x=x0 eine Änderung der
Position r der Partikelladung q. Für den nichzentrosymmetrischen Fall lässt sich 
als Reihenentwicklung
in 
schreiben:
|
|
(6.30) |
Mit
den gemachten Annahmen für SBHM kann die Bewegung einer Bindungsladung qj mit der eindimensionalen Bewegungsgleichung für
die j- te Bindung berechnet werden in Form
|
|
(6.31) |
mit E als externes, zeitabhängiges
optisches Feld und x als die Auslenkung der j-ten
Ladung qj, aus der Ruhelage x0,
entlang der Bindungsrichtung 
. Mit der Dämpfungskonstanten 
wurde die
dissipative Umgebung berücksichtigt. Die Lösungen zweiter und noch höherer
Ordnungen 
lassen sich über
|
|
(6.32) |
und
|
|
(6.33) |
im Rahmen des SBHM- Modells angeben
mit
|
|
(6.34) |
mit 
als die harmonische Polarisation und 
als die nichtlinearen longitudinalen
Hyperpolarisierbarkeiten erster, zweiter bis n- ter
Ordnung. Dies erlaubt uns die lineare Polarisation und die nichtlinearen
Hyperpolarisierbarkeiten der j- ten Bindung neu
anzugeben.
|
|
(6.35) |
|
|
(6.36) |
Damit kann man in einer verkürzten
Notation für nichtzentrosymmetrische Medien schreiben und erhalten einen
allgemein gültigen analytischen Ausdruck für die longitudinale virtuelle
Störung gerader N- ter Ordnung mit
|
|
(6.37) |
Um die SHG Terme in Abhängigkeit der
Kristallkoordinaten messen zu können ist es notwendig das System weit weg von
den Singularitäten zu betrachten, weil der Kristall im Übergangsgebiet für
mehrere Atomlagen (i. d. R. 5- 6 Atomlagen) transparent wird. Deshalb ist
folgende Approximation erlaubt [PAWA05]:
|
|
(6.38) |
wobei noch die Kopplung der
zugehörigen Resonanzen zu berücksichtigen sind.
|
|
(6.39) |
Damit erhält man das vom rotierenden
Kristall emittierte Licht in Kristallkoordinaten zu:
|
|
(6.40) |
mit
|
|
(6.41) |
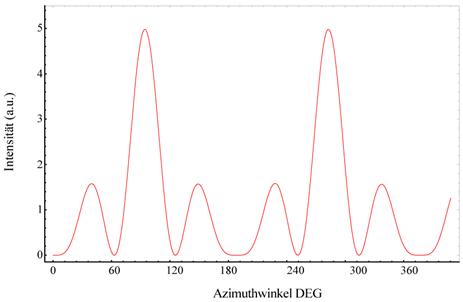
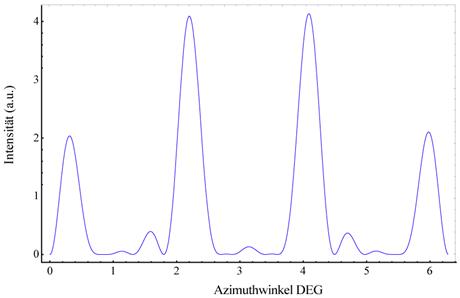
Abbildung 6‑2:
Theoretische Modellberechnung der SHG Spektralgraphen beispielhaft für vicinale 5° (111) Si-SiO2 Oberfläche mit ss- polarisiertem Licht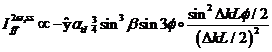 
(oben) und für sp- polarisiertes Licht mit 
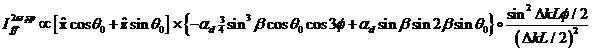(unten) und
Vergleich mit den experimentellen SHG Daten von Lübke et al [LBD94]; α = 11.7x103, L = 3.0, Δk
= 0.667 (s-s): α = 34.0x103,
L = 3.0, Δk = 2.330 (s-p)
bei jeweils 765 nm. Die theoretische Rekonstruierung stimmt mit den publizierten
Ergebnissen überein.
6.5
Diskussion und Zusammenfassung:
Ich beginne mit meinen
Schlussfolgerungen dieses Abschnitts damit, was sich nicht durchführen ließ.
Man bekam keine experimentellen Werte zur Untermauerung der neuen Erkenntnisse
und inwieweit sich diese Erkenntnisse experimentell überhaupt bestätigen bzw.
messen lassen (z. B. Hysterese). Nichts desto trotz konnten die Graphen der
SBHM- Theorie verifiziert und der zugrundeliegende mathematische Formalismus
bestimmt werden. Zudem wurden analytische Ausdrücke für die Hyperpolarisierbarkeiten
und die emittierten hohen Harmonischen von tetraedrisch koordiniertem, optisch
angeregten, vicinalem (111)- Silizium im SBHM- Modell
bestimmt. Es konnte ein analytischer Ausdruck gefunden werden, mit dem es
möglich war, für die verschiedenen Kombinationen der Polarisierbarkeiten die
spektralen SBHM Kurven, in Abhängigkeit der Kristallgeometrie vorherzusagen.
Die erhaltenen Ergebnisse wurden für den Fall 2. Ordnung (SHG) für die ss- und sp-
Polarisationskombinationen mit den experimentellen Daten von Lübke et al. für
SHG verifiziert [LBD94], welche mit den publizierten Ergebnissen übereinstimmen.
Hystereseeffekte konnten hier nicht nachgewiesen werden, weil das von der
Oberfläche emittierte Licht weit weg von Resonanzen, in Abhängigkeit der
Kristallkoordinaten gemessen wurde.
