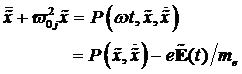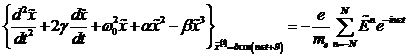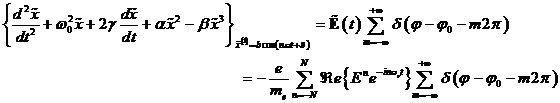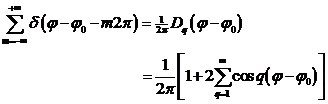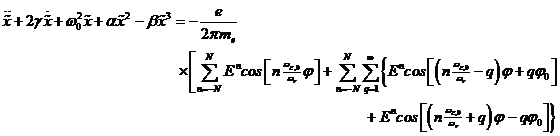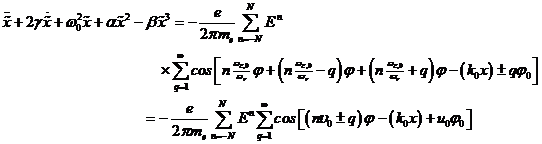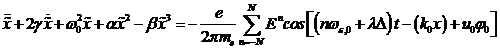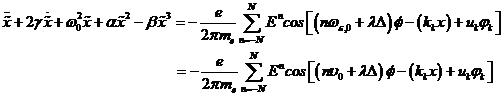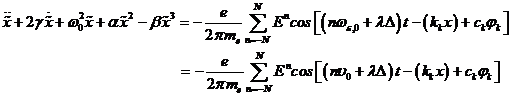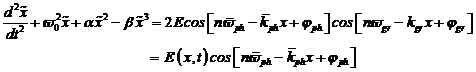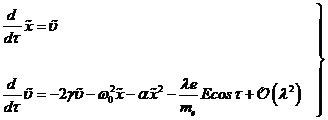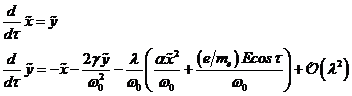| Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie |
|
|
Kapitel
3
Nichtlinearer Elektronenresponse NZS- Materie in der Zeitdomäne
3.1
Einführung
Ein Ziel dieser Arbeit ist es, das
Verhalten der Elektronen beleuchteter Oberflächenmoleküle in der Zeitdomäne und
Fourierdomäne zu verstehen. Die dabei interessierenden
Fragen beziehen sich dabei vorrangig auf die Konstruktion der nichtlinearen
Polarisationswelle, aufgrund der Licht Materie Wechselwirkung, auf der die abgestrahlte
Responsewelle basiert und wie die dazugehörenden Responsetensoren, die nichtlineare
Suszeptibilität und der nichtlineare Brechungsindex aussehen. Dabei beziehen
sich die weiteren Fragen auf den größten realisierbaren Intensitätsresponse an der kondensierten
Materie, in Abhängigkeit der Verstimmung der multichromatischen Photonenfelder
und welche neuen Frequenzen damit erzeugt werden können. Die Beantwortung
dieser Fragen sind die Hauptaufgaben in dieser Arbeit. Zunächst wird in diesem
Abschnitt die zeitliche Dynamik der beleuchteten Grenzflächenelektronen untersucht.
Das dynamische Profil x(t) eines dieser Elektronen im asymmetrischen Potential der
Oberflächenmoleküle kann beschrieben werden durch eine Differentialgleichung 2. Ordnung mit
quadratischer Nichtlinearität.
|
|
(3.1) |
mit ![]() als natürliche
Resonanzfrequenz des j- ten Elektrons des Systems und
als natürliche
Resonanzfrequenz des j- ten Elektrons des Systems und
![]() als einer
periodischen Polynomfunktion der Periodizität 2π
für
als einer
periodischen Polynomfunktion der Periodizität 2π
für ![]() , die man in der Form
, die man in der Form ![]() ansetzen kann. Dabei wird vorausgesetzt, dass die Koeffizienten
ansetzen kann. Dabei wird vorausgesetzt, dass die Koeffizienten ![]() in dieser
endlichen Summe bestimmte Polynome in
in dieser
endlichen Summe bestimmte Polynome in ![]() und
und ![]() sind. Die Lösung
der Bewegungsgleichung wird unendlich für
exakt resonante Elektronen mit ωr = ω0. In der Praxis
treten aber nie unendlich scharfe Linien auf, sondern es liegt vielmehr immer
eine endliche Linienbreite aufgrund von Verunreinigungen oder der natürlichen
Relaxation der Niveaus vor. Diese Effekte können phänomenologisch in unsere
Analyse einbezogen werden, in dem man in (3.1) einen Zerfallsterm
sind. Die Lösung
der Bewegungsgleichung wird unendlich für
exakt resonante Elektronen mit ωr = ω0. In der Praxis
treten aber nie unendlich scharfe Linien auf, sondern es liegt vielmehr immer
eine endliche Linienbreite aufgrund von Verunreinigungen oder der natürlichen
Relaxation der Niveaus vor. Diese Effekte können phänomenologisch in unsere
Analyse einbezogen werden, in dem man in (3.1) einen Zerfallsterm
![]() , einführt mit der Dämpfungskonstanten
, einführt mit der Dämpfungskonstanten ![]() , dem
eine Zerfallszeit des Amplitudenquadrats, also der Intensität der Größe
, dem
eine Zerfallszeit des Amplitudenquadrats, also der Intensität der Größe ![]() entspricht. In den Ausdrücken (3.1) führt das
zu einem zusätzlichen Term von
entspricht. In den Ausdrücken (3.1) führt das
zu einem zusätzlichen Term von ![]() den man zur Resonanzfrequenz addieren muss. Dies führt zur Beseitigung der Singularität in n bzw
ε und einem ausschmieren der Dispersionsfunktion über den Frequenzbereich
der Breite
den man zur Resonanzfrequenz addieren muss. Dies führt zur Beseitigung der Singularität in n bzw
ε und einem ausschmieren der Dispersionsfunktion über den Frequenzbereich
der Breite ![]() . In
Anwesenheit von elektronischen Nichtlinearitäten wird die Konstanz der
Strahlungsdichte zerstört. Dies verursacht eine Verstimmung, die von der
Amplitude linear abhängig ist. Dies wird durch die quadratische Nichtlinearität
in x berücksichtigt. Lässt man diese Eigenschaften mit einfließen, liefert das Polynome
in
. In
Anwesenheit von elektronischen Nichtlinearitäten wird die Konstanz der
Strahlungsdichte zerstört. Dies verursacht eine Verstimmung, die von der
Amplitude linear abhängig ist. Dies wird durch die quadratische Nichtlinearität
in x berücksichtigt. Lässt man diese Eigenschaften mit einfließen, liefert das Polynome
in ![]() und
und ![]() , welche
die oszillierenden Elektronen verschiedener Stärken j in dissipativer Umgebung von
nichtzentrosymmetrischer Materie beschreiben.
, welche
die oszillierenden Elektronen verschiedener Stärken j in dissipativer Umgebung von
nichtzentrosymmetrischer Materie beschreiben.
|
|
(3.2) |
Dabei ist ![]() die Oszillatorstärke
des j- ten Elektrons und α die Stärke der
Nichtlinearität. Der Dämpfungsterm berücksichtigt die dissipative Umgebung der
Elektronen. Das sind die kinetischen
Energieverluste durch Reibung der schwingenden Elektronenorbitale und deren
Umsetzung in thermische Energie. Damit
erhält man das reale Verhalten eines dieser autonomen Elektronen im
nichtlinearen Potential der Moleküle nichtzentrosymmetrischer Materie im bichromatischem Photonenfeld.
die Oszillatorstärke
des j- ten Elektrons und α die Stärke der
Nichtlinearität. Der Dämpfungsterm berücksichtigt die dissipative Umgebung der
Elektronen. Das sind die kinetischen
Energieverluste durch Reibung der schwingenden Elektronenorbitale und deren
Umsetzung in thermische Energie. Damit
erhält man das reale Verhalten eines dieser autonomen Elektronen im
nichtlinearen Potential der Moleküle nichtzentrosymmetrischer Materie im bichromatischem Photonenfeld.
|
|
(3.3) |
wobei die homogene Form mit ![]() die reale Eigendynamik des autonomen Elektrons,
aufgrund der vorhandenen Materieenergie, beschreibt. Photonische Feldripple erzeugen eine zusätzliche Kraft im
Atom, die eine Polarisation bewirkt. Dabei handelt es sich um eine
zeitabhängige Kraft, die zu jeder Zeit auf das Partikel wirkt, welches durch
den Dipol geht. Zur Vereinfachung nehmen wir an, dass es photonische-
Ripple nur in einem Dipol mit definierter Phase
die reale Eigendynamik des autonomen Elektrons,
aufgrund der vorhandenen Materieenergie, beschreibt. Photonische Feldripple erzeugen eine zusätzliche Kraft im
Atom, die eine Polarisation bewirkt. Dabei handelt es sich um eine
zeitabhängige Kraft, die zu jeder Zeit auf das Partikel wirkt, welches durch
den Dipol geht. Zur Vereinfachung nehmen wir an, dass es photonische-
Ripple nur in einem Dipol mit definierter Phase ![]() gibt. Ein
Dipoldurchgang besitzt die Periodizität 2π rad für
gibt. Ein
Dipoldurchgang besitzt die Periodizität 2π rad für
![]() . Die
Bewegungsgleichung in Anwesenheit von photonischen Ripple ist:
. Die
Bewegungsgleichung in Anwesenheit von photonischen Ripple ist:
|
|
(3.4) |
wobei
![]() die Ripple-
Frequenz ist. Die Elektronenfrequenz
die Ripple-
Frequenz ist. Die Elektronenfrequenz ![]() wird für den definierten
Deltawert
wird für den definierten
Deltawert ![]() getroffen. Das heißt, x(t) ist proportional zu einer Delta-Funktion
und damit ist die Reaktion des Festkörpers auf die äußere Störung lokal. Wir können die periodische δ- Distribution
mithilfe des Dirichlet- Kerns zur folgenden
Funktionenfolge entwickeln:
getroffen. Das heißt, x(t) ist proportional zu einer Delta-Funktion
und damit ist die Reaktion des Festkörpers auf die äußere Störung lokal. Wir können die periodische δ- Distribution
mithilfe des Dirichlet- Kerns zur folgenden
Funktionenfolge entwickeln:
|
|
(3.5) |
mit
![]() als Nullphasenwinkel. Für kleine
Nichtlinearitäten hängt die Phase
als Nullphasenwinkel. Für kleine
Nichtlinearitäten hängt die Phase ![]() linear von der Zeit ab. Es gilt:
linear von der Zeit ab. Es gilt:
|
|
(3.6) |
Dies
substituiert in die Bewegungsgleichung ergibt:
|
|
(3.7) |
mit
![]() als der Elektronenfrequenz, d. h. die
natürliche Eigenfrequenz des Systems und
als der Elektronenfrequenz, d. h. die
natürliche Eigenfrequenz des Systems und ![]() als Frequenz des
Ripple- Lichtfeldes. Von allen Frequenzen,
welche auf der rechten Seite im Feldterm dargestellt sind,
wählen wir diese Frequenzen aus, welche in der Nähe der durchgestimmten, d. h.
exakten Elektronenfrequenz ω0 liegen. Die Vernachlässigung
aller anderen Terme vereinfacht die Bewegungsgleichung des Partikels der
Periodizität 2 π im asymmetrischen Potential zu:
als Frequenz des
Ripple- Lichtfeldes. Von allen Frequenzen,
welche auf der rechten Seite im Feldterm dargestellt sind,
wählen wir diese Frequenzen aus, welche in der Nähe der durchgestimmten, d. h.
exakten Elektronenfrequenz ω0 liegen. Die Vernachlässigung
aller anderen Terme vereinfacht die Bewegungsgleichung des Partikels der
Periodizität 2 π im asymmetrischen Potential zu:
|
|
(3.8) |
mit
![]() als zeitlich variierende Frequenz des
Lichtfeldes und
als zeitlich variierende Frequenz des
Lichtfeldes und ![]() als Frequenzverhältnis.
Zur weiteren Untersuchung der zeitlichen Entwicklung des nichtlinearen, optischen
Oberflächenpartikelresponse für kleine Variationen der Lichtfrequenz
als Frequenzverhältnis.
Zur weiteren Untersuchung der zeitlichen Entwicklung des nichtlinearen, optischen
Oberflächenpartikelresponse für kleine Variationen der Lichtfrequenz
![]() , wird
ein kleiner Störparameter λ eingeführt.
, wird
ein kleiner Störparameter λ eingeführt.
|
|
(3.9) |
mit ![]() entsprechend
entsprechend ![]() mit der Nichtlinearität 0 < α<<
1 und Δ als Verstimmungsfaktor. Die zeitliche Abhängigkeit erhält man mit der Näherung
mit der Nichtlinearität 0 < α<<
1 und Δ als Verstimmungsfaktor. Die zeitliche Abhängigkeit erhält man mit der Näherung ![]() :
:
|
|
(3.10) |
Dies
ist die dissipative Bewegungsgleichung. Für den Fall, dass es signifikante Ripple
in N Dipolen gibt sind diese in den Phasen ![]() lokalisiert.
Damit kann die obige Gleichung verallgemeinert werden zu:
lokalisiert.
Damit kann die obige Gleichung verallgemeinert werden zu:
|
|
(3.11) |
und
|
|
(3.12) |
mit ![]() als
Frequenzverhältnis. Dem Elektron wird
durch das äußere optische Feld eine Bewegung aufgeprägt. Dies zeigt
anschaulich, dass das Elektron exakt an der Resonanzfrequenz und deren kleinen
Umgebung zu Schwingungen angeregt werden kann, was die Antwort des Festkörpers
auf ein äußeres Lichtfeld darstellt. Die Anregung hierfür muss nicht
notwendigerweise harmonisch sein, welches aber am effizientesten für den optischen Response ist. Das System wird von der hohen
Unordnung mittels Einstrahlung von Harmonischen zu einem geordneten System
überführt. Soll Licht durch den Kristall gehen oder tiefer eindringen, so muss
man weit weg gehen von der Resonanzfrequenz um Kristalltransparenz zu erzeugen.
Bei multichromatischen Laserexperimenten generiert durch mehrere
Pulsquellen müssen Interferenzeffekte berücksichtigt werden. Unter
Berücksichtigung bichromatischer Fourierkomponenten muss
folgende Differentialgleichung gelöst werden:
als
Frequenzverhältnis. Dem Elektron wird
durch das äußere optische Feld eine Bewegung aufgeprägt. Dies zeigt
anschaulich, dass das Elektron exakt an der Resonanzfrequenz und deren kleinen
Umgebung zu Schwingungen angeregt werden kann, was die Antwort des Festkörpers
auf ein äußeres Lichtfeld darstellt. Die Anregung hierfür muss nicht
notwendigerweise harmonisch sein, welches aber am effizientesten für den optischen Response ist. Das System wird von der hohen
Unordnung mittels Einstrahlung von Harmonischen zu einem geordneten System
überführt. Soll Licht durch den Kristall gehen oder tiefer eindringen, so muss
man weit weg gehen von der Resonanzfrequenz um Kristalltransparenz zu erzeugen.
Bei multichromatischen Laserexperimenten generiert durch mehrere
Pulsquellen müssen Interferenzeffekte berücksichtigt werden. Unter
Berücksichtigung bichromatischer Fourierkomponenten muss
folgende Differentialgleichung gelöst werden:
|
|
(3.13) |
mit
|
|
(3.14) |
wobei
gilt:
|
|
(3.15) |
Dies
beschreibt eine wandernde Welle mit einer niederfrequenten zeit- und ortsabhängigen
Amplitude ![]() und
hochfrequentem Schwingungsterm
und
hochfrequentem Schwingungsterm ![]() . Die Amplitude dieser propagierenden Welle ist
moduliert mit
. Die Amplitude dieser propagierenden Welle ist
moduliert mit ![]() und
und ![]() . Für die weiteren Betrachtungen wird Phasenanpassung
. Für die weiteren Betrachtungen wird Phasenanpassung ![]() vorausgesetzt. Bei
multichromatischen
Laserexperimenten wird die Gruppengeschwindigkeit berücksichtigt, da aufgrund
der hochfrequenten Lichtoszillationen nur die langsamen, zeitgemittelten Variationen
wichtig werden.
vorausgesetzt. Bei
multichromatischen
Laserexperimenten wird die Gruppengeschwindigkeit berücksichtigt, da aufgrund
der hochfrequenten Lichtoszillationen nur die langsamen, zeitgemittelten Variationen
wichtig werden.
3.2
Numerische Lösung: Computer- Physik Details
Für die hier berichtete numerische
Simulation wird der RKF Integrator 4. Ordnung [PFTV92] mit doppelter Präzession
genutzt. Das simulierte System besteht aus einem nichtzentrosymmetrisch
gebundenen 1- Elektronen- System welches mit ein, zwei und mehr optischen
Feldern beliebiger Frequenz beliebiger Kombination beleuchtet wird. Die Resonanzfrequenz
des Systems für Silizium Grenzflächen skaliert in den atomaren Einheiten mit ![]() unter Voraussetzung
der Bindungsenergie des Elektrons im Silizium von 2 eV.
Weitere Parameter sind rotes HeNe- Laserlicht
unter Voraussetzung
der Bindungsenergie des Elektrons im Silizium von 2 eV.
Weitere Parameter sind rotes HeNe- Laserlicht ![]() , der nichtlineare Koeffizient α mit
, der nichtlineare Koeffizient α mit ![]() , wobei
ein typischer Atomabstand der Si - Si - Einfachbindung in Festkörpern 2,5 Ǻ
beträgt und die maximale Elektronenauslenkung mit 2 Ǻ abgeschätzt wurde. Die
spezifische Ladung des Elektrons skaliert in der Größenordnung 2,9205x104
C / u, wobei das E- Feld in V/m berücksichtigt wird. Das Beschleunigungsfeld
, wobei
ein typischer Atomabstand der Si - Si - Einfachbindung in Festkörpern 2,5 Ǻ
beträgt und die maximale Elektronenauslenkung mit 2 Ǻ abgeschätzt wurde. Die
spezifische Ladung des Elektrons skaliert in der Größenordnung 2,9205x104
C / u, wobei das E- Feld in V/m berücksichtigt wird. Das Beschleunigungsfeld ![]() skaliert in der Größenordnung
skaliert in der Größenordnung
![]() .
.
3.3
Numerische Ergebnisse und Diskussion:
Aufgrund der Wechselwirkung des
Teilchens mit dem externen optischen Feld ändert sich der Anfangsbeitrag des
Partikels im Phasenraum mit der Zeit. In diesem Abschnitt wird diese
Zeitentwicklung verfolgt und die Änderung des Response- Beitrags bestimmt. Zu diesem Zweck wird das dynamische
Profil nichtzentrosymmetrisch gebundener Elektronen anhand der Differentialgleichungen
(3.16) numerisch integriert. Dazu wird die nichtlineare inhomogene ODE zweiter
Ordnung (3.3) umgeschrieben, in einen Satz von zwei gekoppelten ODEs erster
Ordnung, mit einer Genauigkeit von ![]() :
:
|
|
(3.16) |
wobei ![]() und
und ![]() mit
mit ![]() gilt. Wie
bereits in Kapitel 2 erwähnt sind die interessierenden Effekte die
Verteilungsgröße im Phasenraum, wenn man die Parameter der eingestrahlten
zeitabhängigen optischen Felder, d.
h. die Feldamplitude E und die Frequenz ωi,
variiert. Im Folgenden wird
der Fall evaluiert, wo die externe Frequenz näherungsweise der linearisierten Frequenz des Partikels entspricht und wir führen
einen Verstimmungsparameter λΔ ein mit:
gilt. Wie
bereits in Kapitel 2 erwähnt sind die interessierenden Effekte die
Verteilungsgröße im Phasenraum, wenn man die Parameter der eingestrahlten
zeitabhängigen optischen Felder, d.
h. die Feldamplitude E und die Frequenz ωi,
variiert. Im Folgenden wird
der Fall evaluiert, wo die externe Frequenz näherungsweise der linearisierten Frequenz des Partikels entspricht und wir führen
einen Verstimmungsparameter λΔ ein mit:
|
|
(3.17) |
Im Folgenden wird die Zeitentwicklung
der nichtlinearen Amplitude des Elektronenresponses numerisch approximiert. Dazu
werden hier durch repräsentative Beispiele, die sich daraus ergebenden speziellen
Effekte gezeigt, die mit der numerischen Integration gefunden wurden. Die interessante
Physik erhält man für nichtlineare verstimmte Systeme d. h. λ ≠ 0
und α ≠ 0. Die Simulation mittels einer mittleren Einstrahlungsfrequenz
(bei zwei und mehr Einstrahlungsfrequenzen) wird hierfür durchgeführt. Die
Verstimmung ist dann definiert mit ![]() mit Δk = 0, d. h. das System ist phasenangepasst. Wir
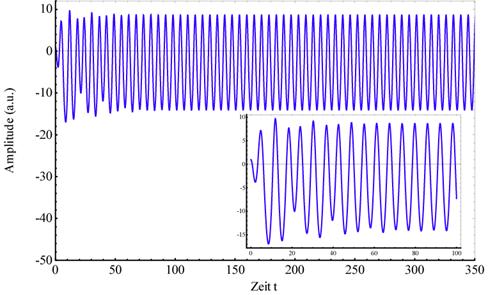
betrachten zunächst schwach gedämpfte Systeme. Die Abbildungen (3.1) und (3.2)
zeigen die zeitliche Entwicklung für die gleiche Erregeramplitude des optischen
Erregerfeldes (E = 41.8) aber unterschiedlicher Verstimmung. Abbildung (3.3)
zeigt die zeitliche Entwicklung für eine kleinere Erregeramplitude des
optischen Feldes (E = 1.0) und der gleichen Verstimmung. Alle 3 Abbildungen
zeigen dass
mit Δk = 0, d. h. das System ist phasenangepasst. Wir
betrachten zunächst schwach gedämpfte Systeme. Die Abbildungen (3.1) und (3.2)
zeigen die zeitliche Entwicklung für die gleiche Erregeramplitude des optischen
Erregerfeldes (E = 41.8) aber unterschiedlicher Verstimmung. Abbildung (3.3)
zeigt die zeitliche Entwicklung für eine kleinere Erregeramplitude des
optischen Feldes (E = 1.0) und der gleichen Verstimmung. Alle 3 Abbildungen
zeigen dass ![]() schnell zu einem Höchstwert ansteigt und sich
dann über einen Relaxationswert für große Zeiten kleinere Oszillationen einstellen.
schnell zu einem Höchstwert ansteigt und sich
dann über einen Relaxationswert für große Zeiten kleinere Oszillationen einstellen.
|
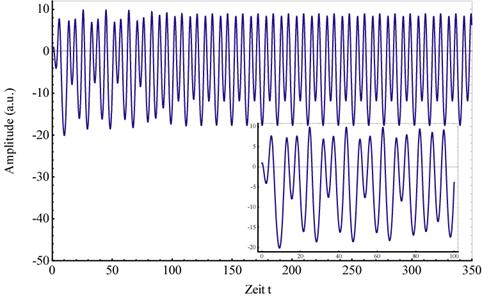
Abbildung
3‑1 zeigt die zeitliche Entwicklung der
Dipolschwingung nichtzentrosymmetrisch
gebundener Elektronen für 55 Perioden; λ = 0.1, α = 0.046165, γ =
0.063, ∆ = -0.1, (ωext =
0.99; ω0 = 1.0), E =
41.803. Der Ausschnitt zeigt die Zeitentwicklung
über 16 Perioden. |
|
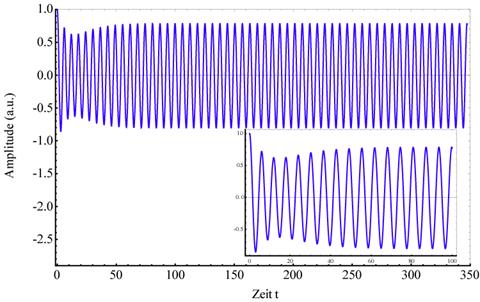
Abbildung
3‑2 zeigt die Entwicklung mit den
gleichen Parametern wie zuvor, aber mit einen anderen Verstimmungsparameter
∆ = +2.25 (ωext = 1.0225; ω0=1.0) |
|
Abbildung
3‑3 zeigt
die Entwicklung mit den gleichen Parametern wie zuvor in Abbildung 6-1, aber
mit einem kleineren optischen Feld E= 1.0; λ = 0.1, α = 0.046165, γ= 0.063. |
Ein Vergleich der Abbildungen (3.1)
und (3.2) zeigt, dass das System mit einem niedrigeren Verstimmungswert länger
braucht bis sich ein Gleichgewichtszustand einstellt, bei konstanter optischer
Feldamplitude; Δ = -1.0 und
Δ = +2.0. Exakt an der Resonanzfrequenz des Systems erhält man die höchste
Anregungsamplitude und somit die höchste Intensitätsemission. Bei der
Einstrahlung mehrerer Frequenzen erhält man nahezu die gleiche
Intensitätsemission wenn eine der Frequenzen die Fundamentale
(Resonanzanregungsfrequenz des Systems) ist. Geht man von der Resonanzfrequenz
weg beobachtet man einen sehr starken Intensitätseinbruch. Die Verstimmung
zwischen den beiden Einstrahlungsfrequenzen beeinflusst die Intensitätsentwicklung
unbedeutend, solange die Interferenzfrequenz im resonanten Bereich liegt. Aus
den Abbildungen (3.1) und (3.3) sowie Abbildung (3.4) lässt sich beobachten,
dass mit einem konstanten Verstimmungswert beide Gleichgewichtswerte und die
Frequenz der Oszillationen nichtlinear zunehmen, wobei die optische Feldamplitude
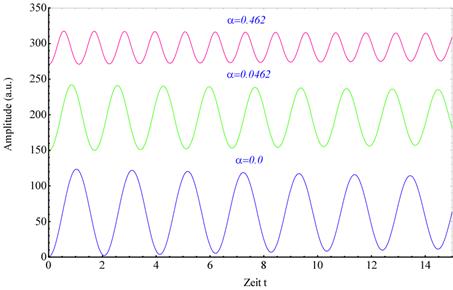
nichtlinear abnimmt. Abbildung (3.4) zeigt die Wechselwirkung von nichtzentrosymmetrischer
Materie mit bichromatischem Laserpuls ![]() in der Zeitdomäne. Unter Berücksichtigung der reinen
Feldamplitude von multichromatischen Laserpulsen ist eine nichtlineare Zunahme
der Oszillationsfrequenz (Mitte und oben) in Abhängigkeit vom
Nichtlinearitätsgrad zu beobachten und erzeugt Frequenzkonversion. Dabei
handelt es sich ausschließlich um einen reinen nichtlinearen Effekt, welcher
für α =0 verschwindet. Für negative Nichtlinearitäten divergiert die
Amplitude. Der Effekt abnehmender Amplituden rührt vom Laserpuls her, welcher
das System nur über die Pulsdauer und nicht permanent anregt. Die Pulsdauer wurde
dabei mit t = 1 genormt. Aufgrund des zeitlich begrenzten Pulses geben die
gezeigten Effekte nur das Kurzzeitverhalten des nichtzentrosymmetrisch
gebundenen Elektrons wieder, wobei hiermit über das Langzeitverhalten keine
weiteren Aussagen getroffen werden können.
in der Zeitdomäne. Unter Berücksichtigung der reinen
Feldamplitude von multichromatischen Laserpulsen ist eine nichtlineare Zunahme
der Oszillationsfrequenz (Mitte und oben) in Abhängigkeit vom
Nichtlinearitätsgrad zu beobachten und erzeugt Frequenzkonversion. Dabei
handelt es sich ausschließlich um einen reinen nichtlinearen Effekt, welcher
für α =0 verschwindet. Für negative Nichtlinearitäten divergiert die
Amplitude. Der Effekt abnehmender Amplituden rührt vom Laserpuls her, welcher
das System nur über die Pulsdauer und nicht permanent anregt. Die Pulsdauer wurde
dabei mit t = 1 genormt. Aufgrund des zeitlich begrenzten Pulses geben die
gezeigten Effekte nur das Kurzzeitverhalten des nichtzentrosymmetrisch
gebundenen Elektrons wieder, wobei hiermit über das Langzeitverhalten keine
weiteren Aussagen getroffen werden können.
|
|
Abbildung 3‑4
zeigt die zeitliche Entwicklung der Wechselwirkung von NZS- Materie mit bichromatischem Laserpuls. Die Nichtlinearität variiert
dabei von α =0 (unten) bis α = 0.046165 (oben). Abhängig vom
Nichtlinearitätsgrad zeigt sich Frequenzkonversion. Zu beachten ist, dass
aufgrund der zeitlich begrenzten Pulsanregung die gezeigten Effekte nur das
Kurzzeitverhalten des Elektrons darstellen und nicht das Verhalten für lange
Zeiten.
3.4
Zeitliche Entwicklung der Elektronen-
Trajektorie im Phasenraum
Um die spezielle
Periodizitätsabhängigkeit zu zeigen, wird die zeitliche Dynamik des
Grenzflächenpartikels mit ![]() umgeschrieben in
ein weiteres System gekoppelter Differentialgleichungen 1. Ordnung der Form:
umgeschrieben in
ein weiteres System gekoppelter Differentialgleichungen 1. Ordnung der Form:
|
|
(3.18) |
mit einer Genauigkeit von ![]() und den
Definitionen
und den
Definitionen ![]() und
und ![]() mit
mit ![]() , wobei
, wobei ![]() der Phasenraum
ist. Damit können Bilder ebener Phasentrajektorien konstruiert werden. Zunächst werden nur kleine optische
Felder zugelassen. Die Forderung kleiner Felder schließt chaotisches Verhalten
im Phasenraum aus und gewährleistet eine Untersuchung im nicht chaotischen
Regime. Wie zuvor gesehen wurde, existieren für nichtzentrosymmetrische Materie
zwei wesentliche Fixpunkte, ein stabiler zentraler Fixpunkt
der Phasenraum
ist. Damit können Bilder ebener Phasentrajektorien konstruiert werden. Zunächst werden nur kleine optische
Felder zugelassen. Die Forderung kleiner Felder schließt chaotisches Verhalten
im Phasenraum aus und gewährleistet eine Untersuchung im nicht chaotischen
Regime. Wie zuvor gesehen wurde, existieren für nichtzentrosymmetrische Materie
zwei wesentliche Fixpunkte, ein stabiler zentraler Fixpunkt ![]() am Minimum und
ein äußerer labiler Fixpunkt
am Minimum und
ein äußerer labiler Fixpunkt ![]() am lokalen
Maximum des Potentials. Dieser äußerste Fixpunkt wird in der Phasentrajektorie
nicht mehr erreicht, weil sich dieser in der Umgebung der Singularität destabilisiert.
Jede nichttriviale Lösung der Differentialgleichung (3.18) besitzt periodische oszillierende
Lösungen in Form periodischer Attraktoren. Die Grenzwertattraktoren können durch Variation der optischen Parameter
erhalten werden. Hierzu wird das nichtzentrosymmetrisch gebundene Elektron zunächst
am zentralen, stabilen Fixpunkt
am lokalen
Maximum des Potentials. Dieser äußerste Fixpunkt wird in der Phasentrajektorie
nicht mehr erreicht, weil sich dieser in der Umgebung der Singularität destabilisiert.
Jede nichttriviale Lösung der Differentialgleichung (3.18) besitzt periodische oszillierende
Lösungen in Form periodischer Attraktoren. Die Grenzwertattraktoren können durch Variation der optischen Parameter
erhalten werden. Hierzu wird das nichtzentrosymmetrisch gebundene Elektron zunächst
am zentralen, stabilen Fixpunkt ![]() gestartet und numerisch
über 232 Perioden bzw. für die Grenzwertattraktoren
über 185 Perioden numerisch integriert. Die erhaltenen nichtanalytischen Lösungen
sind in den Abbildungen (3‑5) bis
(3‑7) für einen repräsentativen
Satz von Parameterwerten der (
gestartet und numerisch
über 232 Perioden bzw. für die Grenzwertattraktoren
über 185 Perioden numerisch integriert. Die erhaltenen nichtanalytischen Lösungen
sind in den Abbildungen (3‑5) bis
(3‑7) für einen repräsentativen
Satz von Parameterwerten der (![]() )- Phasenebene
dargestellt. Es ist zunächst ein nichtlineares Hochschrauben aus dem zentralen
Fixpunkt heraus zu beobachten, welches deutlich von Kreis und Spiralbahnen
abweicht. Dieser Effekt wird umso drastischer, je höher das nichtlineare
Potential ist, indem sich das Elektron befindet, d. h. α bzw. E. Selbst
für zunehmende Nichtlinearitäten α oder höhere photonische
Felder erlangt das nichtzentrosymmetrische System für große Zeiten einen
stabilen Zustand und geht in einen immer stärker deformierteren
Grenzzyklus über (rot).
)- Phasenebene
dargestellt. Es ist zunächst ein nichtlineares Hochschrauben aus dem zentralen
Fixpunkt heraus zu beobachten, welches deutlich von Kreis und Spiralbahnen
abweicht. Dieser Effekt wird umso drastischer, je höher das nichtlineare
Potential ist, indem sich das Elektron befindet, d. h. α bzw. E. Selbst
für zunehmende Nichtlinearitäten α oder höhere photonische
Felder erlangt das nichtzentrosymmetrische System für große Zeiten einen
stabilen Zustand und geht in einen immer stärker deformierteren
Grenzzyklus über (rot).
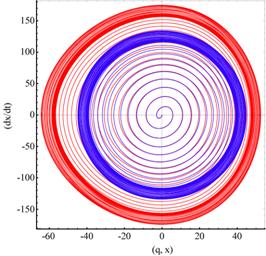
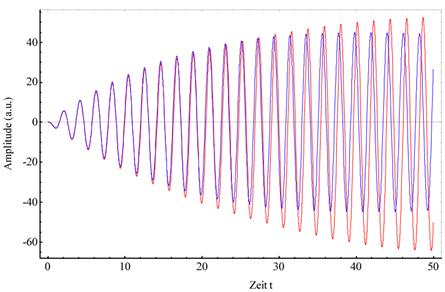
Abbildung
3‑5
zeigt die Trajektorie nichtzentrosymmetrisch gebundener Elektronen im
Phasenraum, (x, v)- Ebene (oben, rote Kurve) und in der Zeitdomäne, (x, t)- Ebene
(unten, rote Kurve), die der Randbedingung ![]() genügt; E=46.0;
α=0.046165 linear, dissipativ γ=0.013,, ωress=
3.0386,, ωextt= 2.7386. Dabei weicht in
Abhängigkeit des Nichtlinearitätsparameters α oder der photonischen Felder
E die Phasentrajektorie deutlich von Spiral- und Kreisbahnen ab, bzw. verläuft
unsymmetrisch bezüglich der Zeitachse. Das harmonische Potential zeigt innerhalb
davon eine Phasentrajektorie in Form von Kreis und Spiralbahnen (oben, blaue
Kurve) bzw. verhält sich achsensymmetrisch bezüglich der t- Achse (unten, blaue
Kurve)..
genügt; E=46.0;
α=0.046165 linear, dissipativ γ=0.013,, ωress=
3.0386,, ωextt= 2.7386. Dabei weicht in
Abhängigkeit des Nichtlinearitätsparameters α oder der photonischen Felder
E die Phasentrajektorie deutlich von Spiral- und Kreisbahnen ab, bzw. verläuft
unsymmetrisch bezüglich der Zeitachse. Das harmonische Potential zeigt innerhalb
davon eine Phasentrajektorie in Form von Kreis und Spiralbahnen (oben, blaue
Kurve) bzw. verhält sich achsensymmetrisch bezüglich der t- Achse (unten, blaue
Kurve)..
Wird das nichtzentrosymmetrisch gebundene
Elektron hingegen am äußeren instabilen Fixpunkt ![]() gestartet, zeigt
sich zu Beginn ein chaotisches Systemverhalten und die Bewegung des Elektrons
ist für die Anfangszeitperiode nicht vorhersagbar (innerste Trajektorieradien,
rot ). Trotzdem werden selbst große negative
Anfangsamplituden vom zentralen, stabilen Fixpunkt angezogen und konvergieren
wieder in einen stabilen Grenzzyklus um diesen Fixpunkt herum, Abb. (3.6).
gestartet, zeigt
sich zu Beginn ein chaotisches Systemverhalten und die Bewegung des Elektrons
ist für die Anfangszeitperiode nicht vorhersagbar (innerste Trajektorieradien,
rot ). Trotzdem werden selbst große negative
Anfangsamplituden vom zentralen, stabilen Fixpunkt angezogen und konvergieren
wieder in einen stabilen Grenzzyklus um diesen Fixpunkt herum, Abb. (3.6).
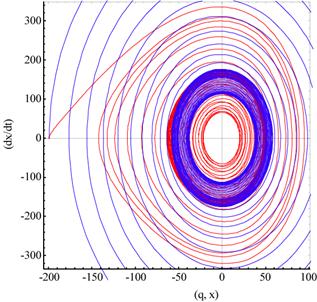
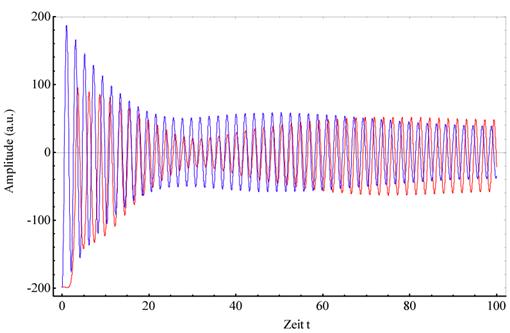
Abbildung 3‑6
zeigt die verhältnismäßig stabilen Phasentrajektorien in der (x, v)- und (x,
t)- Ebene ausgehend vom linken instabilen Fixpunkt ![]() in erhöhter dissipativer Umgebung; γ=0.043, E=6.0, α=0.046165 nichtlinear,
ωres = 3.0386, ωext
= 2.9786. Das Systemverhalten zeigt sich anfangs instabil und ein typischer
weises chaotisches Bild wird erhalten. Selbst für die Wahl großer negativer
Anfangsamplituden in den Randbedingungen besitzt das System einen stabilen Attraktor. Um den zentralen Fixpunkt vollführt das Elektron eine
photonengetriebene Oszillation mit der Frequenz
in erhöhter dissipativer Umgebung; γ=0.043, E=6.0, α=0.046165 nichtlinear,
ωres = 3.0386, ωext
= 2.9786. Das Systemverhalten zeigt sich anfangs instabil und ein typischer
weises chaotisches Bild wird erhalten. Selbst für die Wahl großer negativer
Anfangsamplituden in den Randbedingungen besitzt das System einen stabilen Attraktor. Um den zentralen Fixpunkt vollführt das Elektron eine
photonengetriebene Oszillation mit der Frequenz ![]() .
.
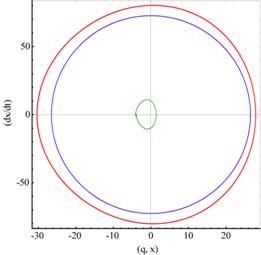
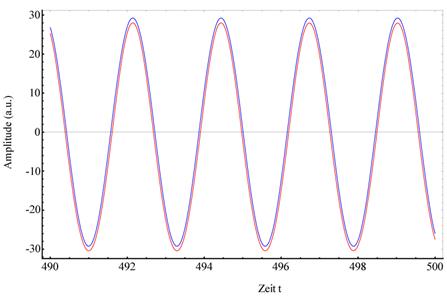
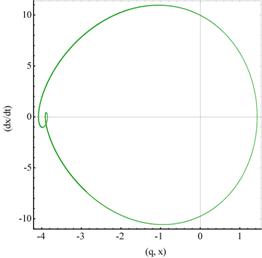
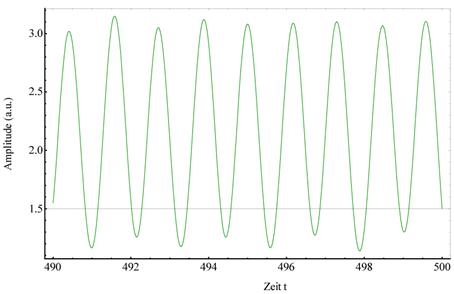
Abbildung 3‑7
zeigt die Bilder der Phasentrajektorien in der (x, v)- und (x, t)- Ebene nichtzentrosymmetrisch
gebundener Materieelektronen im linearen (blau) und nichtlinearen Regime (rot),
sowie deren heraus präparierte nichtlineare Phasentrajektorie und deren
zeitliche Entwicklung (grün). Es zeigt sich deutlich eine Periodenverdoppelungskaskade,
welche ein Charakteristikum nichtlinearer Schwingungen, hier insbesondere der
2- Photonen Resonanz darstellt. Ab dem Degenerationspunkt Dp,
der auf einen Bifurkationspunkt hindeutet, entwickelt sich die 2. Amplitude; E=46.0;
α=0.046165, dissipativ γ=0.013,
ωres = 3.0386, ωext
= 2.7386.
3.5
Diskussion und Zusammenfassung:
In diesem Abschnitt wurde das
Verhalten beleuchteter Elektronen in nichtzentrosymmetrischer Materie analysiert.
Dabei ist die zeitabhängige harmonische
Anregung des Elektrons durch das äußere optische Feld die zu favorisierende
aufgeprägte Bewegung, welche am effizientesten übertragbar ist und den stärksten optischen Response generiert. Zudem geht das
System in einen entropieärmeren Zustand über und ist
somit leichter zu analysieren. Es wurde die Zeitentwicklung der
Amplitude des Elektronenresponses numerisch berechnet. Die interessante Physik erhält man für nichtlinear
aktivierte und verstimmte Systeme, d. h. α ≠ 0 und λ ≠ 0. Mit der numerischen Berechnung der
Zeitentwicklung des Elektronenpartikels wurde gezeigt, dass die Amplitude
des Elektronenresponses, oder entsprechend das
Emissionsvermögen rasch auf
einen Höchstwert ansteigt und dann gegen einen
Gleichgewichtswert relaxiert, wobei sich für
große Zeiten kleinere Oszillationen einstellen. Der Gleichgewichtswert stellt
sich dabei binnen weniger Perioden des externen Feldes ein, wenn die Verstimmung
∆ mit ![]() einen höheren Wert aufweist und braucht
deutlich länger für niedrigere Verstimmungswerte. Dies kann verstanden werden
indem man berücksichtigt, dass das System kleinen Verstimmungen besser folgen
kann und diese nachhaltiger beeinflussen. Bei multichromatischen Laserexperimenten wurde die Gruppengeschwindigkeit
des Laserpulses berücksichtigt, weil langsame Amplitudenvariationen bei der
Untersuchung mit optischen Frequenzen interessant werden. Bei
Einstrahlung mehrerer Frequenzen erhält man nahezu die gleiche Intensitätsemission
wenn eine der Frequenzen die Fundamentale ist. Die Verstimmung zwischen den
beiden Einstrahlungsfrequenzen beeinflusst die Intensitätsentwicklung
unbedeutend, solange die Überlagerungsfrequenz im resonanten Bereich liegt. Das
simulierte bichromatische Laserbeispiel zeigte, unter
Berücksichtigung der reinen Feldamplitude, eine nichtlineare Zunahme der
Oszillationsfrequenz in Abhängigkeit vom Nichtlinearitätsgrad und es wurde Frequenzkonversion
beobachtet. Dabei handelt es sich ausschließlich um einen reinen nichtlinearen
Effekt, welcher für α =0 verschwindet. Für negative Nichtlinearitäten
divergiert die Amplitude. Dabei rührt der Effekt abnehmender Amplituden vom Laserpuls
her, welcher das System nur über die Pulsdauer anregt und danach das System
ausschwingt. Die Untersuchung der zeitlichen Entwicklung der Elektronen-
Trajektorie in der (
einen höheren Wert aufweist und braucht
deutlich länger für niedrigere Verstimmungswerte. Dies kann verstanden werden
indem man berücksichtigt, dass das System kleinen Verstimmungen besser folgen
kann und diese nachhaltiger beeinflussen. Bei multichromatischen Laserexperimenten wurde die Gruppengeschwindigkeit
des Laserpulses berücksichtigt, weil langsame Amplitudenvariationen bei der
Untersuchung mit optischen Frequenzen interessant werden. Bei
Einstrahlung mehrerer Frequenzen erhält man nahezu die gleiche Intensitätsemission
wenn eine der Frequenzen die Fundamentale ist. Die Verstimmung zwischen den
beiden Einstrahlungsfrequenzen beeinflusst die Intensitätsentwicklung
unbedeutend, solange die Überlagerungsfrequenz im resonanten Bereich liegt. Das
simulierte bichromatische Laserbeispiel zeigte, unter
Berücksichtigung der reinen Feldamplitude, eine nichtlineare Zunahme der
Oszillationsfrequenz in Abhängigkeit vom Nichtlinearitätsgrad und es wurde Frequenzkonversion
beobachtet. Dabei handelt es sich ausschließlich um einen reinen nichtlinearen
Effekt, welcher für α =0 verschwindet. Für negative Nichtlinearitäten
divergiert die Amplitude. Dabei rührt der Effekt abnehmender Amplituden vom Laserpuls
her, welcher das System nur über die Pulsdauer anregt und danach das System
ausschwingt. Die Untersuchung der zeitlichen Entwicklung der Elektronen-
Trajektorie in der (![]() )- Phasenebene
im nichtlinearen Regime zeigte, dass jede nichttriviale Lösung der nichtlinearen
Differentialgleichung periodisch oszillierende Lösungen in Form periodischer Attraktoren besitzt. Für kleine Photonenfelder erhält man
Phasentrajektorien in Form von Kreis und Spiralbahnen, wie es kennzeichnend für
einen harmonischen Oszillator ist. Sukzessive Erhöhung der Photonenfelder
bewirkt eine Asymmetrie der Amplitude bezüglich
der Zeitachse. Nichtlineare Phasentrajektorien werden dabei in Abhängigkeit der
externen Photonenfelder zweifach degeneriert, wobei dies
eine Amplitudenaufteilung bewirkt was auf einen Bifurkationspunkt hindeutet.
Oberhalb des instabilen Fixpunkts bei -200 pm wird
die Amplitude instabil und divergiert. Lässt man das, unter dem Einfluss
des nichtzentrosymmetrischen Potentials, schwingende
Elektron, in einer hinreichend kleinen Umgebung am (oder unterhalb) der instabilen Fixpunktauslenkung
los, so rollt es immer in das zentrale Minimum und führt dort um den zentralen
Fixpunkt eine photonengetriebene Oszillation mit der Frequenz
)- Phasenebene
im nichtlinearen Regime zeigte, dass jede nichttriviale Lösung der nichtlinearen
Differentialgleichung periodisch oszillierende Lösungen in Form periodischer Attraktoren besitzt. Für kleine Photonenfelder erhält man
Phasentrajektorien in Form von Kreis und Spiralbahnen, wie es kennzeichnend für
einen harmonischen Oszillator ist. Sukzessive Erhöhung der Photonenfelder
bewirkt eine Asymmetrie der Amplitude bezüglich
der Zeitachse. Nichtlineare Phasentrajektorien werden dabei in Abhängigkeit der
externen Photonenfelder zweifach degeneriert, wobei dies
eine Amplitudenaufteilung bewirkt was auf einen Bifurkationspunkt hindeutet.
Oberhalb des instabilen Fixpunkts bei -200 pm wird
die Amplitude instabil und divergiert. Lässt man das, unter dem Einfluss
des nichtzentrosymmetrischen Potentials, schwingende
Elektron, in einer hinreichend kleinen Umgebung am (oder unterhalb) der instabilen Fixpunktauslenkung
los, so rollt es immer in das zentrale Minimum und führt dort um den zentralen
Fixpunkt eine photonengetriebene Oszillation mit der Frequenz ![]() aus.
aus.