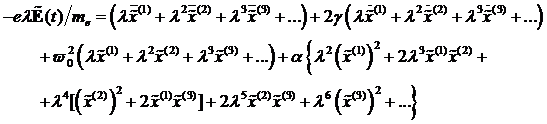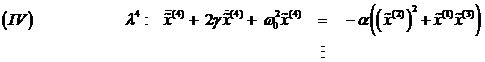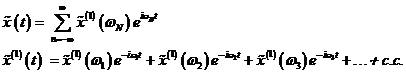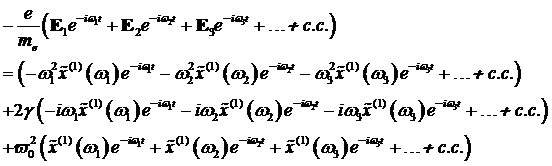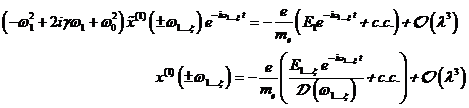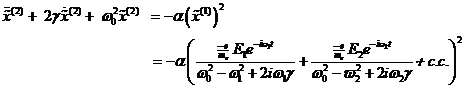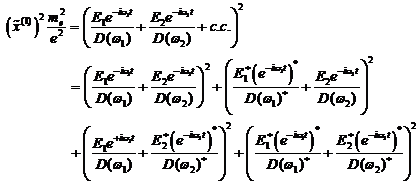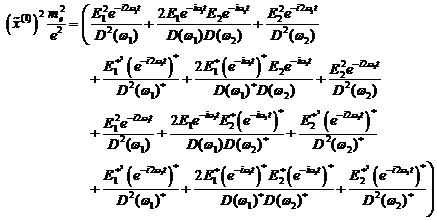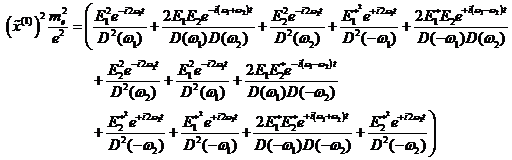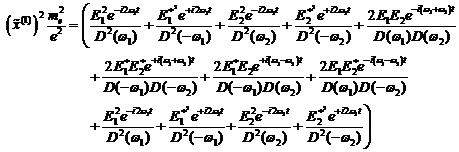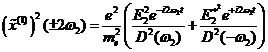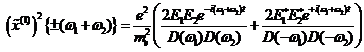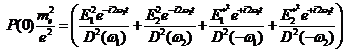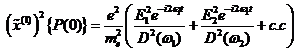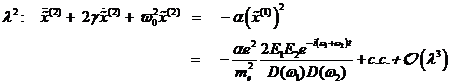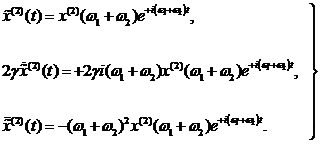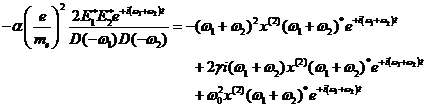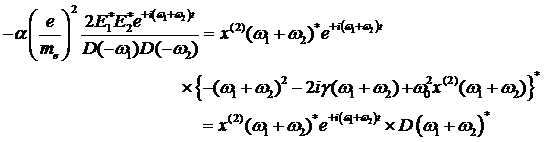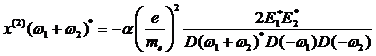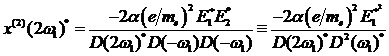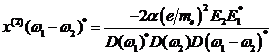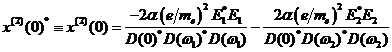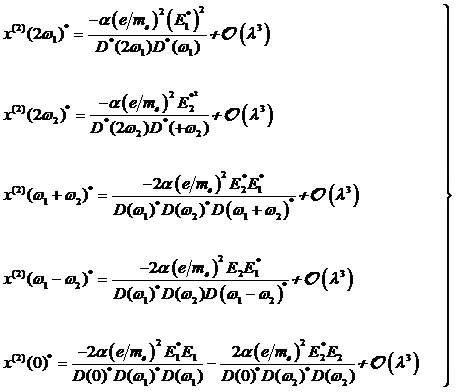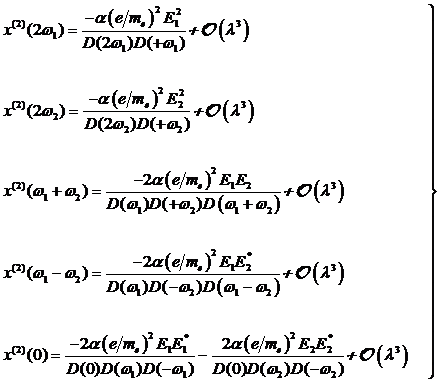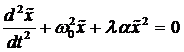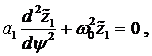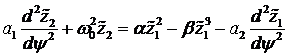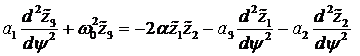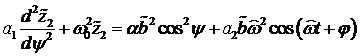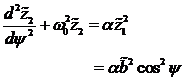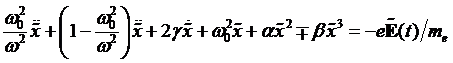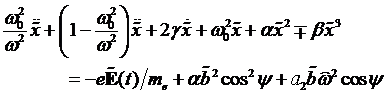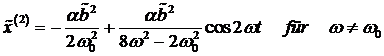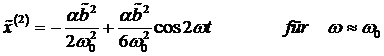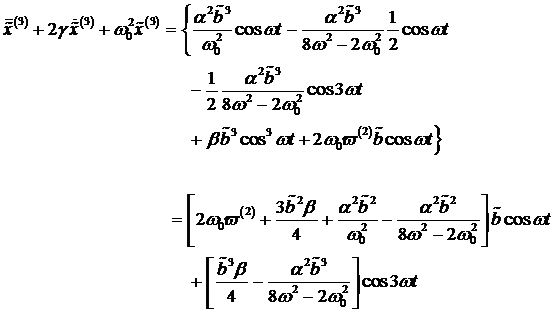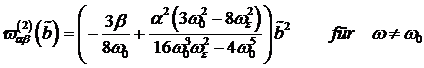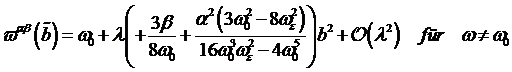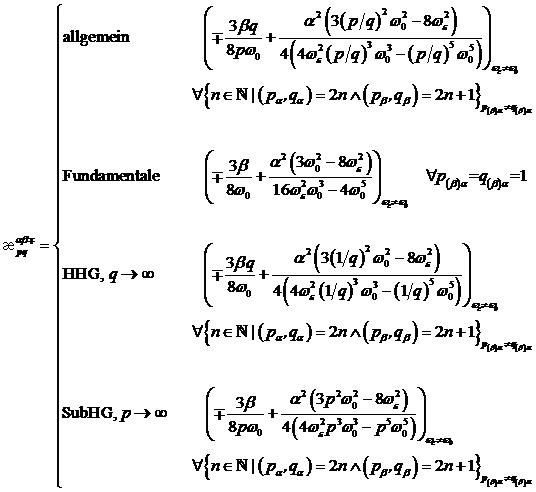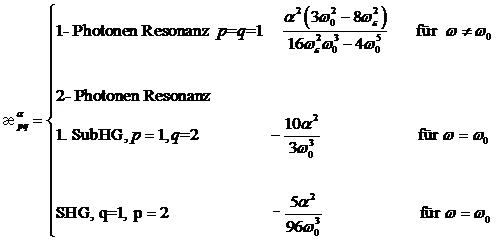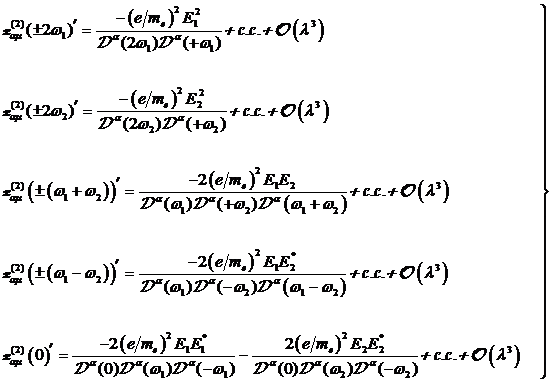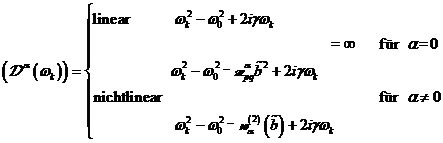Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie

Kapitel 4

Nichtlinearer Elektronenresponse NZS- Materie im Fourierraum

4.1 Einführung

In diesem Abschnitt werden nichtzentrosymmetrisch gebundene, exakt resonante Elektronen ω₀ in multichromatischen photonischen Feldern untersucht. Dazu wird der allgemeine mathematische Formalismus zur Berechnung der 2- Photonen Resonanz, basierend auf der Rayleigh- Schrödinger Störungsrechnung gezeigt und die Ergebnisse diskutiert. Zusätzlich wird der photonenfreie Fall betrachtet. Für genügend schwache optische Felder kann die tatsächliche rücktreibende Kraft, die ein Oberflächenelektron für genügend kleine Oszillationen um den Gleichgewichtszustand erfährt, durch ein harmonisches Potential approximiert werden. Wird die Intensität des eingestrahlten optischen Feldes groß, werden die höheren Terme der Rückstellkraft wichtig und die Bewegung des Elektrons ist nicht länger direkt proportional zum Feld. In dieser Einschränkung kann das Langzeitverhalten des nichtzentrosymmetrisch gebundenen Partikels störungstheoretisch approximiert werden. Dazu wird zur weiteren Untersuchung ein beliebig kleiner Störparameter λ eingeführt gemäß [BRW03]:

(4.1)

mit von elektrischen Multipolen abhängiger nichtlinearer Korrekturkoeffizient als beliebig kleiner Skalar und als Treiberterm. Gibt es nur Quadrupol- und Dipolbeiträge, dann hängt von der Quadrupolstärke erster Ordnung und von der Dipolstärke zweiter Ordnung ab. Die Nichtlinearität kann für atomare Störungen d von etwa einer Atomgröße aus der nichtlinearen Rückstellcharakteristik mit , d. h. bzw. mit , d. h. abgeschätzt werden. Mit und Störungen von erhält man für die Nichtlinearität, in nichtzentrosymmetrischen Kristallen, die konstante Größe von bzw. . Das dynamische Profil des Elektrons x(t) kann durch störungstheoretische Berechnungen bestimmt werden. Dazu wird für die Lösung von ODE (4.1) eine Reihe sukzessiver Näherungen in λ angesetzt:

(4.2)

wobei proportional zum kleinen Treiberparameter ist, entsprechend quadratisch, kubisch und quartär vom kleinen Treiberparameter abhängt. Dabei wird erwartet, dass die Terme, proportional zum jeweiligen Störungsparameter , , …, jede für sich die Bewegungsgleichung erfüllen. Zweimalige Differentiation von (4.2) ergeben die Zeitableitungen der Form:

(4.3)

(4.4)

mit

(4.5)

(4.6)

Substitution von Gleichung (4.3) und (4.4) in die Bewegungsgleichung (4.1) ergibt folgenden Ausdruck:

(4.7)

Jetzt ist es möglich, die entsprechenden Näherungs- Koeffizienten von ,,, …, zu vergleichen um die dazugehörigen Gleichungen zu erhalten. Für jeden Wert von λ ergibt der obige Ansatz eine Lösung, wobei die nicht von λ abhängig sind. Damit ist jeder Term mit gleicher Potenz in λ eine Lösung. Wenn λ groß ist, tragen nur hohe bei und umgekehrt. Sortieren nach Ordnungen von λ führt zu:

(4.8)

(4.9)

(4.10)

(4.11)

Abhängig von der Struktur des Treiberterms entstehen höhere Harmonische und Subharmonische . Alle Betrachtungen und Vorhersagen betreffen die 2. Näherung in . Die erste Gleichung (4.8) entspricht dabei dem linearen Lorentz- Modell und ist das Standardmodell für den Brechungsindex. Wie zuvor erwähnt, besteht das externe Feld aus N- Fourierkomponenten, wobei aufgrund der Linearität der Gleichungen sich die Gesamtlösung aus einer Summe von N- Lösungskomponenten zusammensetzt. Die stationäre Lösung kann durch folgenden Fourieransatz beschrieben werden:

(4.12)

mit für reelle Amplituden. Substitution der beiden Zeitableitungen (4.5) und (4.6) in (4.7) kann insgesamt angeschrieben werden mit:

(4.13)

Vergleich der Fourierkomponenten der l. S. und der r. S. von Gleichung (4.13), ergibt Ausdrücke für die jeweilige Fourieramplitude welche lösbar ist mit

(4.14)

mit der komplexen resonanten Frequenzfunktion , wobei im Resonanznenner, aufgrund der Einbeziehung ihrer c. c. Felder, sowohl positiv als auch negativ sein kann. Für nichtzentrosymmetrische Materie ergeben sich Elektronenresponses gerader Ordnung. Im Fall von zwei Fourierkomponenten des Photonenfeldes gibt es letztendlich Frequenzresponses gemäß der Summenfrequenz- und Differenzfrequenzgeneration und einen Gleichanteil. Der SHG Response für monochromatische photonische Felder kann unter Berücksichtigung der bestimmten zeitlichen Entwicklung des Treiberterms durch Transformation in den Fourierraum gelöst werden. Substitution von (4.12) in (4.9) ergibt:

(4.15)

Dazu muss in dieser Gleichung der quadratische Treiberterm betrachtet werden. Die Lösung liefert dann die entsprechenden neuen "exotischen" Frequenzterme. Im Falle von 2 Fourierkomponenten und deren komplex konjugierten des externen Photonenfeldes kann man folgende zu berücksichtigenden quadratischen Komponenten hinschreiben:

(4.16)

Elementare mathematische Umformungen ergeben folgende Einzelkomponenten mit Exponentialtermen der Form , , , , :

(4.17)

Zusammenfassung und Vereinfachung liefern Exponentialterme der Form , , ,

(4.18)

Sortieren der einzelnen Fourierkomponenten und Klassifizierung der einzelnen Terme führt neben den neuen Responses, bei der doppelten Frequenz ±2ω₁, ±2ω₂ auch noch zu Summen- und Differenzenfrequenzen ±(ω₁+ω₂), ±(ω₁−ω₂) und einem Gleichanteil DC. Die Fourier Amplitude x⁽²⁾ setzt sich also aus der Summe all dieser Komponenten zusammen.

(4.19)

Damit können die neuen Treiberterme mit einer Genauigkeit bis zu kleinen Größen zweiter Ordnung in Abhängigkeit der generierten Frequenzen angegeben werden:

Doppelte Frequenz (SHG) , :

(4.20)

(4.21)

Summenfrequenzerzeugung (SFG) :

(4.22)

Differenzfrequenzerzeugung (DFG) :

(4.23)

Gleichanteil (DC):

(4.24)

(4.25)

Zur Bestimmung des Summenresponse in mit den Frequenzen erhält man durch Berücksichtigung der entsprechenden Frequenz- Treiberterme.

(4.26)

Dabei entspricht der für die positive Frequenzkomponente zu berücksichtigende Treiberfeldterm , der komplex konjugierte Term den negativen Fourierkomponenten . Die stationäre Lösung für die Summenfrequenzerzeugung und deren zeitlichen Ableitungen für c. c. Felder sind von der Form

(4.27)

Substitution von (4.27) in (4.26) ergibt für komplex konjugierte optische Felder:

(4.28)

Elementare mathematische Umformungen liefern einen Ausdruck, welcher für alle Zeiten t erfüllt sein muss.

(4.29)

Dies ist nur der Fall, wenn der Klammerausdruck in (4.29), welcher der komplexen Frequenzfunktion für Summenfrequenzerzeugung (SFG) entspricht, sich aufhebt. Damit ergibt sich die Fourieramplitude für SFG zu:

(4.30)

für identische Frequenzen kann sofort auf die negative Fourierkomponente der zweiten Harmonischen geschlossen werden.

(4.31)

Analog zur mathematischen Modellierung von SFG erhält man die Ausdrücke für die Fourieramplitude für DFG für den negativen Differenzfrequenzbereich zu:

(4.32)

Werden wiederum identische Frequenzen betrachtet so ergibt sich daraus der Gleichanteil c. c. zu:

(4.33)

Insgesamt erhält man hiermit zwei Sätze von "exotischen" Ausdrücken zur Beschreibung der Wechselwirkung von bichromatischem Licht mit zentrosymmetrischer Materie, welche Singularitäten bzw. in dissipativer Umgebung behobene Singularitäten bei den Frequenzen ±2ω₁, ±2ω₂, ±(ω₁+ω₂), ±(ω₁−ω₂) generieren. Für die negativen Frequenzkomponenten läßt sich folgender Satz von Gleichungen anschreiben

(4.34)

bzw. ihrer c. c. komplex konjugierten photonischen Felder für den positiven Frequenzbereich:

(4.35)

Die Fourieramplitude Amplitude setzt sich wiederum aus der Summe all dieser Komponenten zusammen.

4.2 Asymptotischer Aufbau des Elektronenresponse

Bei vollständigem Fehlen externer optischer Felder liegt eine regellose freie thermische Bewegung des Elektronenpartikels vor. Exakt resonante Partikel sind entropiearm und deren Verhalten ist zeitlich vorhersagbar. Diese bestimmen das Langzeitverhalten der Materieelektronen. Zur weiteren Untersuchung des Langzeitverhaltens wird ein beliebig kleiner, positiver Störparameter λ eingeführt. Die stationäre Amplitude der Oberflächenelektronen in zweiter Näherung, d. h. mit einer Genauigkeit bis zu kleinen Größen der Ordnung λ³ wird bestimmt mit:

(4.36)

Mit (1.18) bis (1.27) im Kapitel 1 Methoden können die Funktionen und die Größen mit folgenden Gleichungssystem bestimmt werden.

(4.37)

(4.38)

(4.39)

aus (4.37) findet man mithilfe der Modifikation für hohe Harmonische mit n als Integer

(4.40)

und insgesamt:

(4.41)

Damit erhält man aus (4.38) den Ausdruck:

(4.42)

wobei keine Additionstheoreme möglich ist und sich aufhebt für . Damit gibt es keinen Elektronen- Skew in der linearen Näherung nichtzentrosymmetrischer Materie. Bemerkenswert ist in diesem Zusammenhang, dass für zentrosymmetrische Medien bereits in erster Näherung kleiner Größen mit ein Skew mit nachgewiesen werden kann. Wir setzen und erhalten:

(4.43)

Aus der asymptotischen Näherung stationärer Lösungen erhalten wir über die Beziehungen und mit der Phasenänderung und die lineare Lösung für . Dies entspricht einer allgemeinen Lösung mit den Randbedingungen x₀ = b₀ und , d. h zur Zeit t = 0 liegt nur die maximale Auslenkung b vor. Damit diese Lösung, die anharmonische Bewegungsgleichung (4.1) in dissipativer Umgebung streng erfüllt, muss diese umgeschrieben werden in die Form:

(4.44)

wobei die Identität benutzt wurde. Mithilfe der Ergebnisse der asymptotischen Methode können wir die Frequenzabweichung vom linearen Verhalten bestimmen. In zweiter Näherung kleiner Größen erhalten wir:

(4.45)

Die Berücksichtigung freier Partikel in der sukzessiven Näherung und liefert über und mit der trigonometrischen Identität für die 2. Näherung kleiner Größen den zu integrierenden Ausdruck:

(4.46)

Die inhomogene, lineare Gleichung wird für freie Partikel unter der Bedingung für das Fehlen eines Resonanzgliedes auf der rechten Seite integriert. Damit können wir Null setzen und die Integration liefert mit für das konstante Glied . Wenn die Lösung erster Ordnung ein sinnvoller Startpunkt ist, dann führt unsere allgemeine Argumentation von vornherein in den allgemeinen Ansatz für und zu setzen. Mit der obigen Argumentation wird der durch die Integration entstehende sin- Term komplex und berücksichtigt die Dämpfung bzw. Absorption und der cos- Term ist real und beschreibt die Amplitude. Mit diesen Annahmen erhalten wir als Lösung zweiter Näherung kleiner Größen:

(4.47)

(4.48)

Die Berücksichtigung der nächsthöheren Ordnung liefert mit der Lösung zweiter Näherung kleiner Größen die Frequenzkorrektur zur natürlichen Frequenz des Systems. Mit der sukzessiven Näherung und finden wir für die dritte Näherung kleiner Größen die analytische Lösung für nichtresonante Erregerfrequenzen

(4.49)

und für resonante Erregerfrequenzen:

(4.50)

Die Korrektur zur Fundamentalen erhalten wir aus den Koeffizienten des Resonanzterms welcher das nichtlineare Verhalten an der Oberfläche - Bulk - Schnittstelle wiedergibt.

(4.51)

Daraus lässt sich leicht erkennen, dass zentrosymmetrische und nichtzentrosymmetrische Materie einen negativen Skew aufweisen. Betrachtet man nun positiv dotierte Bulkfestkörper (), so genügt diese der modifizierten Differentialgleichung zweiter Ordnung . Dabei wurde berücksichtigt, dass der Bulk mit Schnittstelle nicht invariant ist unter der Transformation . Somit ergibt sich dieselbe Lösungsstruktur wie für den undotierten Bulk, wobei nur noch die Inversion des Nichtlinearitätsparameters bzw. der Frequenz berücksichtigt werden muss. Damit erhält man zwei konkurrierende Skews des elektronischen Response bezüglich mit

(4.52)

Für nichtzentrosymmetrische Medien ist die amplitudenabhängige Frequenzkorrektur dem Quadrat der Schwingungsamplitude proportional und . Analog erhält man in für zentrosymmetrische Medien (Bulk) mit eine Frequenzkorrektur positiver Skewness, bzw. für dotiertes Volumenmaterial negative Skewness, welche jeweils dem Quadrat der Schwingungsamplitude proportional sind.

4.3 Singularitäten NZS Materie

In diesem Abschnitt werden die möglichen nichtlinearen Resonanzfälle NZS- Materie betrachtet. Nach Voraussetzung liegen die 1- bzw. 2- Photonenresonanz, d. h. allgemein die höheren Harmonischen und Subharmonischen hinreichend nahe bei der natürlichen Resonanzfrequenz. Im Limes ist , . Nach Setzen der Variablentransformation und , lassen sich allgemeingültige Ausdrücke für die nichtlinearen Koeffizienten zentro- und nichtzentrosymmetrischer Materie über deren Schnittstelle, in der Näherung kleiner Größen bis 2. Ordnung formulieren gemäß:

(4.53)

mit den Skewnesskoeffizienten der Anharmonizität, , welche mit undotierten und mit positiv dotierten Festkörperbulk berücksichtigt. Dabei ist zu beachten, dass für die Anharmonizitätspaare im nichtlinearen Regime, , nichtzentrosymmetrische Materie an Singularitätsstellen gerader Ordnung und undotierte bzw. negativ dotierte zentrosymmetrische Materie an Singularitätsstellen ungerader Ordnung jeweils mit negativer Skewness skaliert. Für positiv dotierte zentrosymmetrische Materialien sowie deren Schnittstelle Oberfläche / Bulk ist zu berücksichtigen, dass die Nichtlinearität ein vollständiges Vorzeichen durchläuft und sich demzufolge eine Skewnessumkehr ergibt. Damit lässt sich die exakte Lösungsstruktur für die nichtlineare Amplitude, Suszeptibilität bzw. Brechungsindex, sowie der nichtlinearen Polarisation in den jeweiligen Näherungen finden. Dabei ist zu berücksichtigen, dass mit einer Genauigkeit von in die Berechnungen mit eingeht. Somit kann man für die jeweilige Materiegeometrie, in der Näherung kleiner Größen bis 2. Ordnung, gültig für Frequenzintervalle , den exakten Verlauf des nichtlinearen optischen Response für beliebig hohe Harmonische und Subharmonische vorhersagen. Die betrachtete 1- Photonen und 2- Photonen Resonanz nichtzentrosymmetrischer- Materie im Fourierraum lässt sich für mit der nichtlinearen Skelettkurve exakt angeben, wobei sich die nichtlinearen Responsekoeffizienten ergeben zu:

(4.54)

Bemerkenswert ist hierbei, dass für die hohen Harmonischen die Skewness immer mehr zunimmt, ganz im Gegensatz zu den Subharmonischen deren Skewness- Betrag immer weiter abnimmt. Diese Modellbildung stellt eine enorme Verbesserung des bisherigen nichtlinearen Modells dar (siehe z. B. [BRW03, Kapitel 1]), in der die Nichtlinearität nicht nur approximiert wurde, sondern in ihrem innersten Wesen exakt mathematisch berücksichtigt wurde. Dabei wird die Transformation der nichtlinearen Resonanzfunktion vorgeschlagen, wobei zusätzlich berücksichtigt werden muss, dass bzw. wird. Dies ergibt sich, wenn die exakt auftretenden Singularitäten in den störungstheoretischen Berechnungen berücksichtigt werden. Für die nichtlineare Amplitude lässt sich damit folgender modifizierter Satz von Gleichungen für nichtzentrosymmetrische Materie angeben.

(4.55)

mit der exakten komplexen, nichtlinearen Resonanzfunktion:

(4.56)

Bemerkenswert bei diesen Gleichungen ist, dass die Nichtlinearität in die Frequenzfunktion im Nenner eingeht und nicht, wie in der aktuellen Literatur (siehe z. B. [BRW03, Kapitel 1]), lediglich als Proportionalitätsfaktor, der die Amplitude nur lorentzförmig beeinflusst. Zusätzlich muss für den Nichtlinearitätsparameter mit berücksichtigt werden, dass nichtzentrosymmetrische Materie nicht invariant ist unter der Transformation . Dies impliziert die Tatsache, dass die Orientierung des nichtlinearen Skewness- Effekts aufgrund der quadratischen Amplitudenabhängigkeit für nichtzentrosymmetrische Materie rein frequenzabhängig ist. Zur weiteren Erforschung nichtzentrosymmetrischer Materie wird die mathematische Struktur in der zugrundeliegenden Modellbildung mit den Gleichungen (4.53) bis (4.56) betrachtet und deren berechnete Konfiguration in den Abbildungen (4‑1) bis (4‑10) dargestellt, wobei eine vertiefte Untersuchung zentrosymmetrischer Materie geführt wird, in Punkten, wo sich diese Materiearten charakteristisch unterscheiden. Das nichtzentrosymmetrische System, welches dabei zunächst zwei unabhängigen photonischen Feldern, mit den Fourierkomponenten und ausgesetzt war, wird im Folgenden für monochromatische Fourierkomponenten betrachtet. Zur Einordnung dieser Lösungen wird das nichtzentrosymmetrische und zentrosymmetrische System zusätzlich mittels computerphysikalischen Methoden numerisch modelliert. Die Abbildungen (4‑1(a), (b)) zeigen die charakteristischen Eigenschaften, Variationen der störungstheoretisch ermittelten komplexen nichtlinearen Amplitude parallel und antiparallel zur Nichtlinearität α, (α > 0 bzw. α < 0) in Abhängigkeit ihrer photonischen Fourierkomponenten. Es werden zunächst nur kleine optische Felder zugelassen um chaotisches Systemverhalten im Fourierraum auszuschließen, sodass eine Untersuchung des Systems im nicht chaotischen Regime sichergestellt werden kann. Für das so konfigurierte System erhält man zunächst für monochromatische Photonenfelder , neben der 1- Photonen Resonanz an der Systemfrequenz eine weitere charakteristische Resonanz an der halben natürlichen Systemfrequenz, welche durch zwei resonante Photonen hervorgerufen werden (schwarzer Kurvenverlauf, gestrichelt). Die 1- Photonen Resonanz zeichnet sich durch eine Nullstelle, d. h. einen unendlich schmalen Amplitudeneinbruch zwischen den beiden Emissionskanälen aus. Zudem zeigt sich an der Fundamentalen eine rotverschobene Flankenabsenkung. Dies zeigt anschaulich, dass der nichtlineare Elektronenresponse ein schmales transparentes Frequenzfenster besitzt und letztendlich niederfrequentere Strahlung emittiert. Dieses durch Phasenfokussierung erzeugte transparente Fenster ist eine charakteristische Signatur für bosonische Systeme. In der zugrundegelegten Modellbildung, entspricht das dem, 1s - 2s- Übergang.

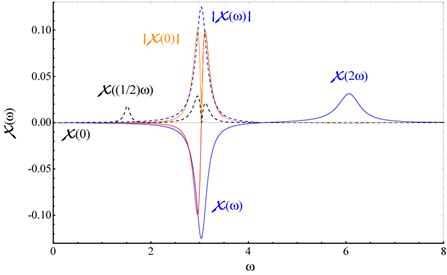
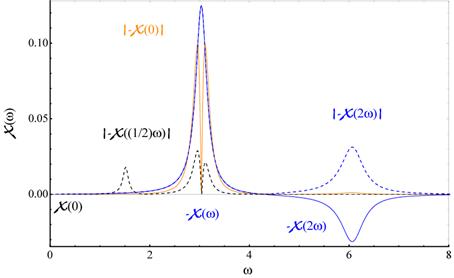
Abbildung 4‑1: Charakteristischer Verlauf der parallelen, α > 0 (oben), bzw. antiparallelen (α < 0) (unten) komplexen nichtlinearen Amplitude (blau) und deren nichtlinearer Betrag (orange). Der qualitative Verlauf ist oben zusätzlich mit eingezeichnet (rote Kurve). Für 1- Photonen Resonanz, vor Reziprozierung der Fourierkoeffizienten erhält man neben einem Transparenzfenster eine blau- und rotverschobene Flankendeformation. Dabei überträgt der höherfrequente Emissionskanal die Information schwächer. Dies deutet auf eine asymmetrische Amplitudenentwicklung hin, in der die Amplitudeninformation zu niederfrequenten Bereichen verschoben wird (negativer Skew). Die blaue Kurve (gestrichelt) zeigt jeweils das übliche Resonanzverhalten, welche sich auszeichnet für reziproke Fourierkoeffizienten; γ=0.13494, |α|=0.046165, ω₀=3.0386 , E=1.0.

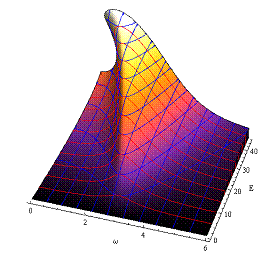
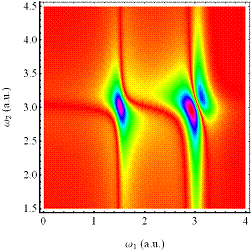
Zur Veranschaulichung der gebildeten Strukturen werden diese zusätzlich in der 2 dimensionalen Fourierebene und im Raum dargestellt. Die zugrundeliegenden Berechnungen wurden dazu in höherer dissipativer Umgebung (γ = 0.23) durchgeführt, um die markanten Effekte besser zeigen zu können. Beachtenswert ist die zusätzliche 2- Photonen Resonanz bei ω = ω₀/2 auf der rotverschobenen Seite des Spektrums, welche zunehmend ausbleicht bzw. die blauverschobene 2- Photonen Resonanz für optische c. c.- Felder, die sich zunehmend färbt und das jeweils verstärkt für hohe Ordnungen. Die nachfolgenden Abbildungen zeigen dies zusätzlich in Perspektivischer Darstellung.

Abbildung 4‑2: Intensitätsdichteverteilung der behobenen Singularitätsstellen als Kontur- Plot für die 1- Photonen und 2- Photonen Resonanz; Der zugrundeliegende qualitative Verlauf der komplexen Amplitude mit Nullstelle (oben) und deren Betrag mit Transparenzfenster (unten) sind zusätzlich jeweils mit ihren c. c.- Feldern abgebildet. Die punktsymmetrische Amplitudenumkehr für die c. c. Felder sind (jeweils links) dargestellt. Es zeigt sich ein für 1- Photonen Resonanz ein verstärkter, rotverschobener, bleichender Übertragungskanal bzw. respektive für c. c. Felder blauverschobener, färbender Kanal; hochdissipativ γ=0.23494, ω₀ = 3.0386, E=1, α=0.046165.

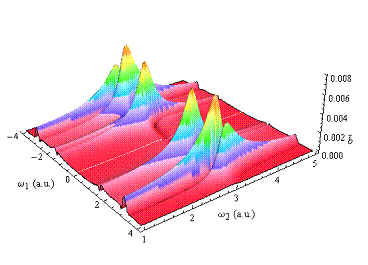
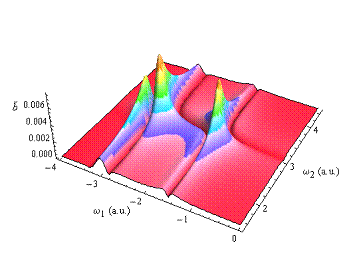
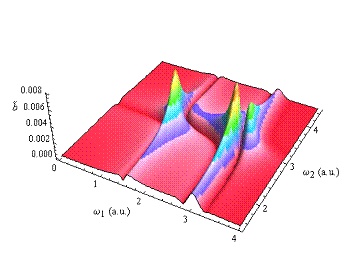
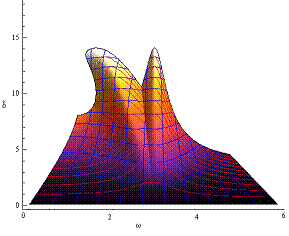
Abbildung 4‑3: Perspektivische Darstellung des nichtlinearen Betrags der spatialen komplexen Amplitude zusätzlich mit c. c.- Feldern (oben) und deren Separation (Mitte und unten) als Funktion der photonischen Erregerfrequenzen. Die Aufteilung der Fundamentalen 1- Photonen Transparenzfenster in die verkleinerten blauverschobenen bzw. die stärker ausgeprägten rotverschobenen Flanken (für c. c. umgekehrt) sind deutlich erkennbar. Die 2- Photonen Resonanz zeigt diese Besonderheit nicht. Mit zunehmender Ordnung färbt sich die 2- Photonen Resonanz, bzw. bleicht aus für optische c. c.- Felder; γ=0.23494, α = 0.046165, ω₀=3.0386, E=1.

Bemerkenswert ist, dass sich im Falle der Anwesenheit von 2- Photonen- Resonanz eine verkleinerte blauverschobene Flanke zeigt (für c. c.- Felder rotverschoben). Dieser Effekt verstärkt sich weiter, wenn die 2- Photonen Resonanz unterdrückt wird, durch Erhöhung des Gleichanteils gemäß → bzw. → und noch ausgeprägter durch deren vollständige Eliminierung gemäß → bzw. → . Nach Reziprozierung der Summenfrequenz zeigt sich Frequenzkonversion, wobei die 2- Photonen Resonanz an der halben Systemfrequenz verschwindet. Bemerkenswert ist in diesem Fall, dass die rotverschobene Flankendeformation und somit die niederfrequente Informationsverschiebung vollständig behoben wird und ein Transparenzfenster zeigt, wie in Abbildung (4‑4) ersichtlich ist.

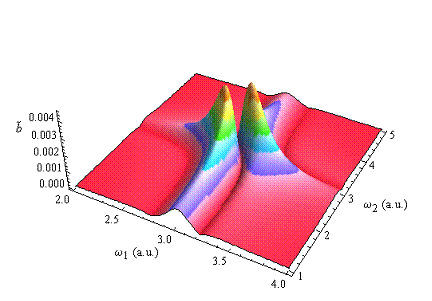
Abbildung 4‑4: zeigt die spezielle Behebung der charakteristischen rotverschobenen Flankendeformation an der komplexen 1- Photonen Resonanzstelle mit Transparenzfenster nach Reziprozierung der Fourierkoeffizienten der Summenfrequenz. Die 2- Photonen Resonanz wurde aus Darstellungsgründen ausgeblendet, weil deren komplexe Amplitude nach Reziprozierung im Vergleich zur Fundamentalen zu schwach ausgeprägt ist; γ=0.23494, α = 0.046165, ω₀=3.0386, E=1.0.

Zu beachten sind die gleichmäßig ausgeprägten Flanken der Fundamentalen, sowie der 2. Harmonischen. Sowohl die blauverschobene als auch die rotverschobene Flanke weisen dieselbe Ausprägung auf. Damit stehen nun zwei gleichwertige Emissionskanäle zur Verfügung. Durch die Behebung der doppelten Singularität verschwindet das Transparenzfenster. Die sich ergebenden Kurven verlaufen an diesen Stellen nun stetig und weisen gewöhnliches Resonanzverhalten auf. Ein weiteres Ziel dieser Arbeit ist es, das exakte (nicht angenähert, wie bei [BRW03, Kapitel 1]) nichtlineare Verhalten des beleuchteten Grenzflächenelektrons an der Resonanzstelle und deren Umgebung im Fourierraum zu verstehen. Aufgrund der nichtlinearen Wechselwirkung des Teilchens mit hinreichend starken externen optischen Feldern ändert sich der Resonanzbeitrag des Partikels im Fourierraum, in Abhängigkeit zur Frequenz. Im Folgenden wird diese Frequenzentwicklung verfolgt und die Änderung des Response- Beitrags bestimmt. Zu diesem Zweck werden hier, durch ein repräsentatives Beispiel, die sich daraus ergebenden speziellen Effekte aufgezeigt, die analytisch und mithilfe der numerischen Integration gefunden wurden und vergleichen diese mit den Lösungen, wie sie in der aktuellen Literatur (siehe hierzu z. B. [BRW03, Kapitel 1]) publiziert sind. Zunächst wird die numerisch berechnete Resonanzentwicklung nichtzentrosymmetrischer Medien mit quadratischer Nichtlinearität in Wechselwirkung mit bichromatischem HeNe- Laserlicht, , an der Singularität betrachtet und in den Abbildungen (4‑5) bis (4‑10) gezeigt. Im Vergleich dazu wird die störungstheoretisch gefundene analytische Lösung im Fourierraum für dieselbe Erregeramplitude des bichromatischen optischen Erregerfeldes gezeigt. Die Literatur- Lösung entspricht dabei dem Fall α = 0. Die interessante Physik erhält man für nichtlinear aktivierte Systeme d. h. α ≠ 0. Offensichtlich kippt die Resonanzkurve bei hohen Anregungsamplituden und man erkennt einen Sprung in der Kurve. Dazwischen zeigt sich eine Unschärfe im Hystereseverhalten in der Umgebung der Singularitätsstelle mit verändertem Linienverlauf und veränderter Linienbreite.

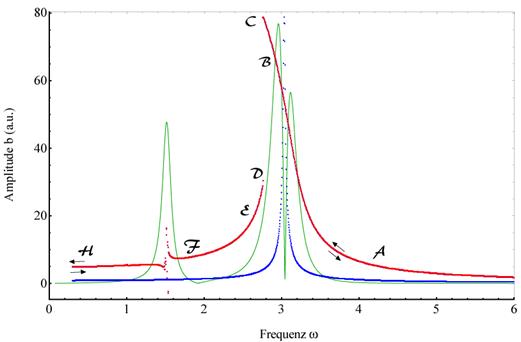
Abbildung 4‑5 zeigt den charakteristischen Verlauf des nichtlinearen Amplitudenbetrags nichtzentrosymmetrischer Materie (grün) in der bisherigen aktuellen nichtlinearen Modellbildung (siehe z. B. [BRW03]) im Vergleich zur numerischen, linearen (blau) und nichtlinearen Lösung (rot). Es ist deutlich die Aufteilung in eine schwächer ausgeprägte rotverschobene Flanke (rechts) und einen blauverschobene Emissionskanal zu erkennen; γ=0.013494, E = 7.5, α = 0.046165, ω_ext=2.9786, ω₀=3.0386. Für den Fall vollständig fehlender Nichtlinearität, α = 0, zeigt die Response Funktion im Fourierraum gewöhnliche Resonanz bei , wie sie charakteristisch für Lorentz- Materialien sind. Unter Berücksichtigung quadratischer Nichtlinearität, , zeigt sich ein neues dispersives Resonanzverhalten. Für nichtzentrosymmetrische Materie mit erhält man mit zunehmender Amplitude eine harte Potentialcharakteristik und die Kurve zeigt negative Skewness.

Die im Fourierraum numerisch untersuchte ()- Kurve NZS- Systeme weist in Abhängigkeit der optischen Erregerfrequenzen Schwingungen mit Hysteresecharakter auf. Variiert man ω von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die Amplitude der erregten Schwingung entlang des "unteren Astes" FED bis sie im Punkt D, in der Umgebung der Singularitätsstelle über einen geringen Unschärfebereich ausschmiert. Bei weiterer Erhöhung der Erregerfrequenzen springt die Amplitude im Punkt D auf den Wert von Punkt B, d. h. es existiert nur noch eine Lösung auf dem „oberen Ast“ mit negativer Tangente. Das System muss unstetig auf diesen übergehen. Bei weiterer Erhöhung der Frequenz verringert sich die Amplitude stetig entlang des "oberen Astes" BA. Verringert man jetzt wieder die Frequenz so wächst die Amplitude entlang des oberen Astes AB bis man zu C (bmax) kommt. Im Punkt C reißt die Amplitude ab und sie fällt sprunghaft auf den Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren Astes EF der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung (gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch die Punkte DC mit senkrechter Tangente abgegrenzt.

Der abgearbeitete Algorithmus ist dabei invariant gegenüber einer Inversion bezüglich des Nichtlinearitätskoeffizienten α → - α für gerade Potenzen des nichtlinearen Terms in x. In Abbildung (4‑6) ist die spezielle Änderung der komplexen nichtlinearen Amplitude nichtzentrosymmetrisch gebundener Elektronen beim Übergang vom linearen ins nichtlineare Regime in der Fourierdomäne gezeigt. Die Berechnungen wurden am Beispiel von Si in Wechselwirkung mit bichromatischem HeNe- Laserlicht durchgeführt. Dabei bleiben die zuvor diskutierten Eigenschaften erhalten, wobei diese aber nun in einer kleinen Umgebung um ihre Singularität mit der Frequenz stark variieren. Für diese Untersuchung wurde zum einen von kleinen Frequenzen kommend und zum anderen von hohen Frequenzen kommend, links- und rechtsseitig an die Singularitätsstelle angenähert numerisch über 237 Perioden integriert.

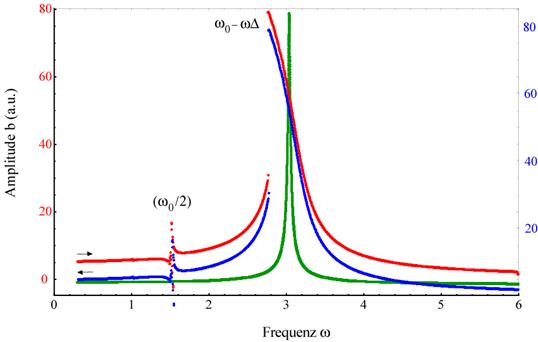
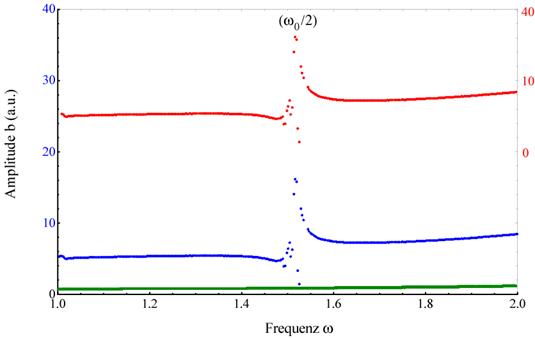
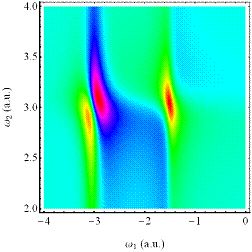
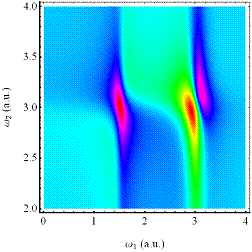
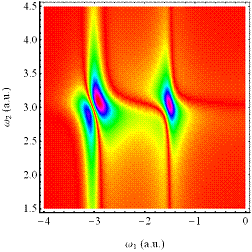
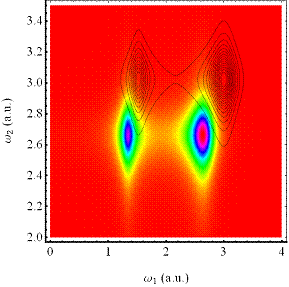
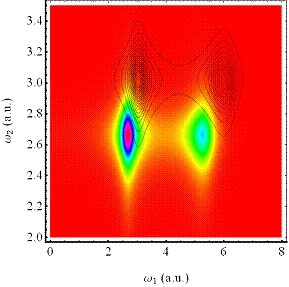
Abbildung 4‑6: Intensitätsdichteverteilung der 1- Photonen und 2- Photonen Resonanz und deren reziprozierten Ordnung der Fourierkomponenten zur Generation der höheren Harmonischen (SHG) im Vergleich zum harmonischen Response für α = 0. Abhängig von der Materiesymmetrie zeigt sich Frequenzkonversion nur für geradzahlige Harmonische (rechts). Der Harmonische Response ist als Konturlinien- Plot (oben rechts) mit berücksichtigt. Dabei dienen die Konturlinien der 2- Photonen Resonanz nur zur Veranschaulichung des Skewness- Effekts. Für den harmonischen Response bleibt dieser aus und es ergibt sich nur die 1- Photonen Resonanz (links). Die Abweichung vom harmonischen Response zeigt den Skew, der nur im nichtlinearen Fall auftritt. Im Gegensatz zur Literatur- Lösung [BRW03], in der die Nichtlinearität als Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der Intensität Einfluss nimmt, kann mit der hier erhaltenen Lösung und dem entwickelten Algorithmus auch exakt die Skewness der Amplitude bzw. Intensität vorhergesagt und beschrieben werden. Die spezielle Änderung der Imaginärteile der nichtlinearen Amplitude x_i beim Übergang vom linearen (grüne Kurve) ins nichtlineare Medium in der Fourierdomäne (rot und blau gekennzeichnet) wird darunter gezeigt (Mitte). Dabei ergeben sich für die linkseitige und rechtsseitige Näherung an die Singularität identische Kurven. ROT: von kleinen Frequenzen kommend; BLAU: von hohen Frequenzen kommend (aus Darstellungsgründen leicht versetzt eingezeichnet). Es zeigt sich zusätzlich zur 1- Photonen- Resonanz, eine 2 Photonen Resonanz bei ω₀/2. Der harmonische Response zeigt sich dabei besser abgestimmt als die nichtlinearen Responses, welche größere Frequenzverteilungen aufweisen. (unten) Vergrößerungs- Ausschnitt der erhaltenen 2- Photonen Resonanz für die Integration über 474 Perioden des Photonenfeldes; γ=0.013494, E = 7.5, α = 0.046165, ω_ext=2.9786, ω₀=3.0386.

Die genaue Untersuchung der 2- Photonen Resonanz lässt für schwach gedämpfte Systeme, wie im Fall des Si- Kristalls, eine Nullstelle vermuten, was ebenfalls ein Transparenzfenster bedeuten würde. Die nachfolgenden Abbildungen (4‑7) bis (4‑10) zeigen die charakteristischen Änderungen des komplexen Elektronenresponses beim Übergang vom nichtlinearen nichtzentrosymmetrischen Medium (Oberfläche) ins nichtlineare zentrosymmetrische Medium (Bulk, positiv dotiert und undotiert), im Fourierraum. Dabei kann abhängig von der Materiesymmetrie eine spezielle Änderung der nichtlinearen Amplitude xi in Abhängigkeit der Frequenz beobachtet werden, wobei die zuvor diskutierten Eigenschaften erhalten bleiben, diese nun aber in einer kleinen Umgebung um ihre Singularitätsstellen bzw. mit der Frequenz charakteristisch variieren. Zunächst bleibt beim Übergang von der Oberfläche in den negativ dotierten oder undotierten Bulk die negative Skewness erhalten. Dabei weist der undotierte bzw. negativ dotierte Bulk aber einen deutlich schwächeren Skewnesseffekt auf. Beim Photonen- Übergang undotierter Oberflächen in positiv dotierte zentrosymmetrische Materie, gemäß ODE , hingegen stellt sich ein positiver Skew ein. Dabei durchläuft die Skewness ein vollständiges Vorzeichen. Es zeigt sich zusätzlich zur 1- Photonen- Resonanz, eine 2 Photonen Resonanz bei ω₀/2 und eine 3- Photonen Resonanz bei w0/3. Die Berechnung wurde am Beispiel des Si- Kristalls in Wechselwirkung mit bichromatischem und trichromatischem HeNe- Laserlicht und für monochromatische Photonenfeldern durchgeführt.

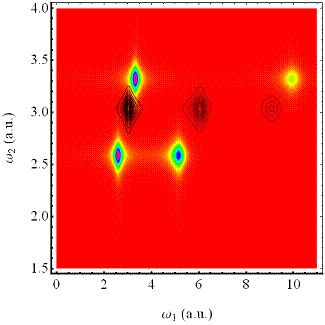
Abbildung 4‑7: Nichtlinearer skewnessbehafteter komplexer Elektronenresponse im extrem nichtlinearen Regime; α=1.46165, γ=0.13, E=1.0x10⁶, ω₀=3.0386, b=80. Ganz oben sind die Amplitudendichten als Funktion der Frequenz für zentro- bzw. nichtzentrosymmetrische Materie (unten) im extrem nichtlinearen Regime gezeigt. Die Amplituden werden für höhere Harmonische extrem klein. Deshalb wurde die Amplitudenverteilung um die 2. und 3. Harmonischen aus Darstellungsgründen höher gewichtet. Die lineare Intensitätsverteilung ist entsprechend als Konturlinie berücksichtigt, wobei die Konturen für SHG und THG zur Darstellung der Skewness mit eingezeichnet wurden (Mitte).

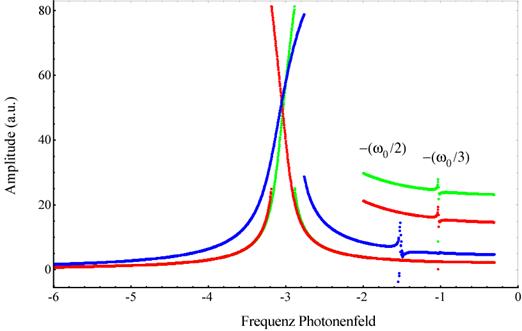
Abbildung 4‑8: Qualitativer Verlauf der komplexen nichtlinearen Amplitude für verschiedene Materiesymmetrien in Wechselwirkung mit bi- und trichromatischen c. c.- Feldern, welche unterschiedliches nichtlineares Verhalten zeigen. Dies zeigt sich insbesondere in Bezug auf ihre Skewnessorientierung und Generation der höheren Photonenresonanzen. Die speziell skewnessbehaftete komplexe nichtlineare Amplitude nichtzentrosymmetrischer (blaue Kurve) und undotierter bzw. negativ dotierter zentrosymmetrischer Materie (grüne Kurve, ) zeigt negative Skewness. Dabei ist bemerkenswert, dass für positiv dotierten Bulk, , (rote Kurve, ), die Skewnessorientierung nicht erhalten bleibt. Die Nichtlinearität durchläuft dabei ein vollständiges Vorzeichen und macht deren Einfluss deutlich sichtbar. Zudem ergibt sich Frequenzkonversion. Abhängig von der Materiesymmetrie werden nur höhere geradzahlige bzw. ungeradzahlige Photonenresonanzen generiert (links unten und rechts oben). Die 3- Photonenresonanz macht sich erst für erhöhte Nichtlinearitätsparameter β um 2 Größenordnungen, Faktor 100, bemerkbar; γ=0.0135, E=7.5, α=0.046165, ω_ext=2.979, ω₀=3.0386.

Um die korrekte Funktionsweise der entwickelten Lösungsstruktur zu validieren und die Gültigkeit der numerischen Lösung einzuordnen, wird die Singularitätslösung, wie in Abschnitt 4.2 beschrieben, herangezogen und mit den numerischen Ergebnissen verglichen. Die Ergebnisse sind in den Abbildungen (4-9 und 4-10) dargestellt. Es ergeben sich Singularitätskurven, welche ganz speziell von der Ordnung der Subharmonischen, wie auch hohen Harmonischen abhängen. Dabei ergibt sich für die Grundresonanz eine Skelettkurve der Form , welche sich in ihrer Skewness ganz signifikant von der Skelettkurve für 2- Photonen Resonanz der Form unterscheidet. Die Ergebnisse werden in hervorragender Weise durch die numerische Integrationslösung bestätigt. Bedenkt man dass eine Frequenz einer Energie entspricht, so lässt sich die von den Symmetrieeigenschaften abhängige, frequenzabhängige Amplitude des Materieresponses energetisch deuten. Nach der hier, in dieser Arbeit durchgeführten nichtlinearen Modellbildung besitzt nichtzentrosymmetrische Materie einen negativen Response, welcher einer Frequenzabnahme und somit auch einer Energieabnahme in der Umgebung der Singularitätsstelle entspricht. Danach antworten Oberflächen auf ihre Anregung mit negativer Skewness und senken somit ihre Energie. Damit können sich Oberflächen besser stabilisieren und höhere Energien aushalten, bevor ihre Struktur, z. B. durch Schmelzen, zerstört wird. Die negative Skewness verleiht demnach nichtzentrosymmetrischer Materie erhöhte Stabilität um sie z. B. zur Katalyse, Oberflächenreaktionen und planare mikrooptische Bauteile besser nutzbar machen zu können. Im Umkehrschluss bedeutet dies, dass der Übergang von undotiertem oder negativ dotiertem Festkörperbulk mit negativem Skew zu positiv dotiertem Bulk, mit der zugrundeliegenden Skewnessumkehr zu positiver Skewness, mit zusätzlicher Bulkanregung antwortet. Somit kann dotierte zentrosymmetrische Materie besser angeregt werden, hätte aber ohne diese zugrundeliegende Skewnessumkehr theoretisch einen höheren Schmelzpunkt. Höhere Harmonische, z.B. die zweite Harmonische, haben in dem untersuchten Modell aufgrund deren Erzeugung im Resonanzgebiet nur eine geringe Eindringtiefe. Dies zeigt anschaulich, dass das erhaltene emittierte Signal zum großen Teil an der Oberfläche erzeugt wird.

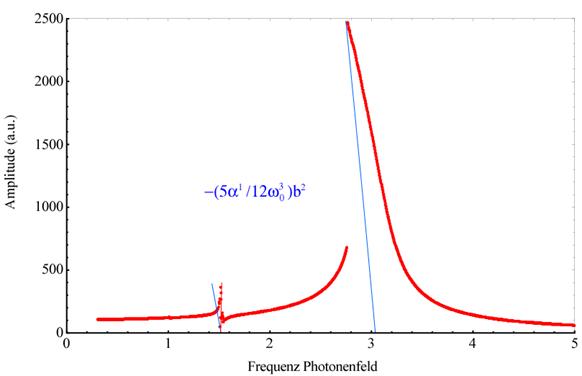
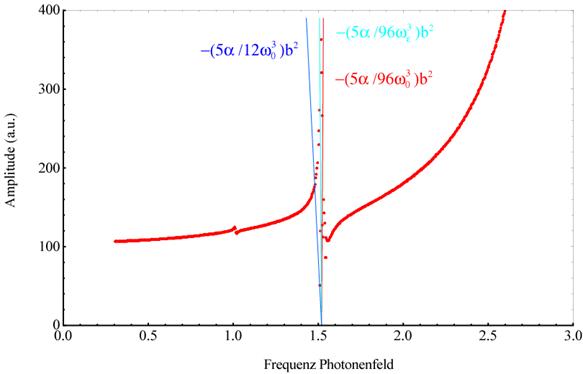
Abbildung 4‑9 zeigt den Skew nichtzentrosymmetrischer Materie zusammen mit den Singularitätslinien. Die rote Singularitätslinie spiegelt die Skewness der 1. Subharmonischen wieder, dazu die blaue Singularitätslinie zum Vergleich ist gemäß der Skewness der Fundamentalen stärker geneigt. Dies macht deutlich, dass der Skewness- Effekt abhängig von der Art und Ordnung (SubHG und HHG) der Singularitätsstelle, bzw. deren behobene Singularität, unterschiedlich ausgeprägt ist. Als Ergebnis erhält man für α → α² eine sehr gute Bestätigung der auftretenden Skewness. Damit wird die entwickelte analytische Lösung hervorragend bestätigt; γ=0.013494, E=162.5, α = 0.046165, ω_ext=2.979, ω₀=3.0386.

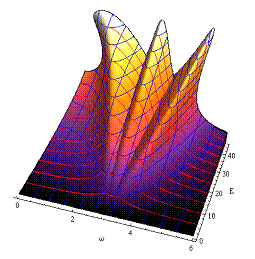
Abbildung 4‑10: Spatiale Darstellung der skewnessbehafteten, nichtlinearen 1- Photon- Elektron Wechselwirkung nichtzentrosymmetrischer Materie, welche die richtige Orientierung des Responses berücksichtigt (oben). Die durch die 2- Photonen Resonanz nach Reziprozierung der Ordnung ihrer Fourierkomponenten hervorgerufene 2. Harmonische (SHG) wurde zusätzlich unter Berücksichtigung optischer c. c.- Felder berechnet (Mitte links). Zusätzlich dargestellt ist die skewnessbehaftete 3- Photonen Resonanz undotierter zentrosymmetrischer Materie bei (1/3) ω₀ (Mitte, rechts). Die 1- Photon- Elektron- Resonanz für den harmonischen und nichtlinearen Response undotierter nichtzentrosymmetrischer und positiv dotierter zentrosymmetrischer Materie in Perspektive, zeigt anschaulich die Skewnessumkehr (unten). Zusätzlich ist das "übliche" harmonische Resonanzverhalten berücksichtigt; Hochdissipativ γ=0.43, α=0.046165, ω₀=3.0386.

4.4 Diskussion und Zusammenfassung:

Die Auswertung der mathematischen Struktur nichtzentrosymmetrischer Materie in der zugrundeliegenden Modellbildung ergab im Fourierraum folgende nichttriviale Ergebnisse: Für monochromatische Photonenfelder erhält man neben der 1- Photonen Resonanz an der Systemfrequenz eine weitere charakteristische Resonanz an der halben natürlichen Systemfrequenz. Für 1- Photonen Resonanz erhält man vor Invertierung der Fourierkomponentenordnung neben einem Transparenzfenster eine blau- und rotverschobene Flankendeformation. Dabei überträgt der höherfrequente Emissionskanal schwächere Informationen. Dies zeigt eine asymmetrische Amplitudenentwicklung im nichtlinearen Regime, in der die Amplitudeninformation zu niederfrequenten Bereichen verschoben wird (negativer Skew). Nach Invertierung der Summenfrequenz zeigt sich Frequenzkonversion, wobei die 2- Photonen Resonanz an der halben Systemfrequenz verschwindet und bemerkenswerterweise die rotverschobene Flankendeformation behoben wird. Damit stehen nun zwei gleichwertige Emissionskanäle zur Verfügung. Das gewöhnliche Resonanzverhalten verläuft an diesen Stellen nun stetig. In der Fourierdomäne wurden anhand der Rayleigh- Schrödinger Störungsrechnung exakt resonante Elektronen, ω₀ = ω_r, im nichtlinearen Regime untersucht, welche für die Generation hoher Harmonischer und Subharmonischer gerader Ordnung verantwortlich ist. Für den photonenfreien Fall wurde der exakte Verlauf der Singularitätskurve analytisch bestimmt. Die analytische Untersuchung des asymptotischen Elektronenresponses zeigte einen neuen exotischen Effekt. Aufgrund der nichtlinearen Wechselwirkung des Teilchens mit hinreichend starken externen optischen Feldern ändert sich der Resonanzbeitrag des Partikels im Fourierraum in Abhängigkeit der Frequenz. Für nichtzentrosymmetrische Medien stellt sich eine frequenzabhängige Amplitude mit negativer Skewness ein. Dieser negative Skewness Effekt wurde mittels der nichtlinearen Skelettkurve gezeigt, welche an der Singularität existiert. Dabei ist der Skewnesseffekt nicht alleine auf nichtzentrosymmetrische Materie begrenzt. Zentro- und nichtzentrosymmetrische Materie skaliert im nichtlinearen Regime mit negativer SKEWNESS und positiv dotierte zentrosymmetrische Materie, sowie der Übergang Oberfläche / Bulk mit positiver SKEWNESS. Die Untersuchung der Skewness höherer Harmonischer zeigte, eine Skewness welche sich in Abhängigkeit von der Ordnung der Harmonischen ändert. Bemerkenswert ist hierbei, dass für die hohen Harmonischen die Skewness immer mehr zunimmt, ganz im Gegensatz zu den Subharmonischen und Ultrasubharmonischen deren Skewness- Betrag immer weiter abnimmt. Um die korrekte Funktionsweise der entwickelten Lösungsstruktur zu validieren und die Gültigkeit der numerischen Lösung einzuordnen, wurde die Singularitätslösung herangezogen und mit der numerischen Lösung verglichen. Dabei konnten die erhaltenen Ergebnisse hervorragend bestätigt werden.

Diese "exotischen" Materieantworten können nach den bisherigen Erkenntnissen darin begründet sein, dass Oberflächen zur Stabilisierung ihre Energie mittels negativer Skewness absenken können und somit in die Lage versetzt werden höhere Energien auszuhalten, bevor ihre Struktur, z. B. durch Schmelzen, zerstört wird. Positiv dotierte Bulkmaterialien antworten aufgrund ihrer umgekehrten Skewness mit zusätzlicher Bulkanregung. Somit kann der Bulk zwar besser angeregt werden, hätte aber ohne diese Skewnessumkehr theoretisch einen höheren Schmelzpunkt, wie es für undotierten bzw. negativ dotierten Bulk der Fall ist. Im Kontext zur Störungsrechnung konnte mit der singulären Lösung eine Verbesserung der bisherigen Theorie erreicht werden indem das bisherige Modell soweit verfeinert wurde, dass mit der hier erhaltenen Lösung und den entwickelten Programmen auch exakt die Skewness der Amplitude bzw. Intensität vorhergesagt und beschrieben werden kann. Dies stellt eine enorme Verbesserung der bisherigen Modellbildung dar, in der die Nichtlinearität nur als Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der Intensität Einfluss nimmt, nicht aber deren frequenzabhängige Amplitudenvariation berücksichtigt.