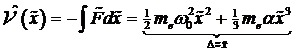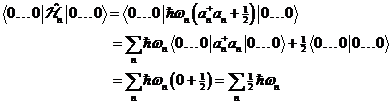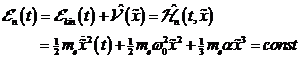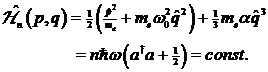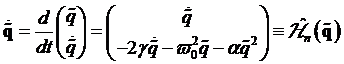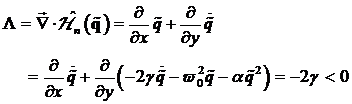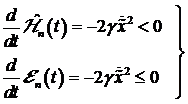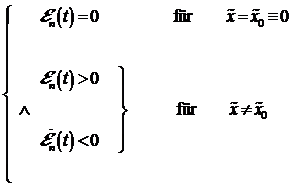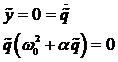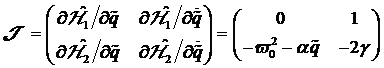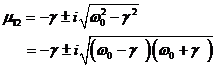| Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie |
          |
Kapitel
2
Hamilton´sche- Struktur nichtzentrosymmetrischer
Materie
2.1
Potential nichtzentrosymmetrisch
gebundener Elektronen
In
diesem Abschnitt wird das unbeleuchtete System, d. h. 
, untersucht. Die nichtlineare
Rückstellkraft der Oszillatoren entspricht
einer harten Charakteristik.
|
|
(2.1) |
Die Annahme, dass der Mediumresponse ohne Verzögerung, d. h. sofort erfolgt, impliziert
durch die Kramers- Kronig- Beziehungen auch, dass das
Medium zwingenderweise dämpfungsfrei und dispersionslos sein muss. Wenn es
keine Dämpfung gibt 
kann die nichtlineare,
elektronische Rückstellkraft integriert werden zu:
|
|
(2.2) |
Das
sich daraus ergebende nichtlineare Potential setzt sich aus dem harmonischen
Potential und einem anharmonischen Korrekturterm zusammen.
Es werden demnach gerade und ungerade Kräfte in 
zugelassen. Dieses Modell beschreibt die
Physik der Elektronenbewegung in realen Materialien, weil das aktuelle
Potential, das die Elektronen spüren, nicht perfekt parabolisch ist. In
realen Kristallen zeigt sich das Wechselwirkungspotential zwischen benachbarten
Atomen unsymmetrisch um die Ruhelage und weißt aufgrund des starken abstoßenden
Potentials für kleine Abstände Asymmetrie auf, bei der der Schwerpunkt der
Schwingungszustände wächst, während er bei einem ungestörten Parabelpotential
unverändert bleibt und es keine Wechselwirkung zwischen den Phononen gibt. In einem Kristall liegt nun eine Vielzahl
von Eigenfrequenzen 
vor. Mit
abnehmender Temperatur verbleibt eine immer größere Zahl dieser Oszillatoren im
Grundzustand und deren Schwingungsfreiheitsgrade werden immer mehr ausgefroren.
|
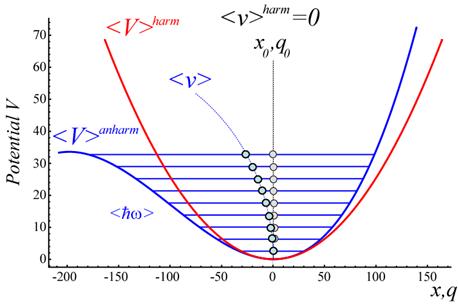
Abbildung
2‑1 zeigt
das anharmonische Potential
nichtzentrosymmetrischer Medien mit quadratischer Nichtlinearität, welches
zum o. g. nichtlinearen Kraftgesetz gehört. Das
harmonische Potential (quadratische Approximation) ist zum Vergleich mit eingezeichnet.
Die quantisierten Energiezustände sind mit berücksichtigt. |
Hier soll die Quantisierung
des elektromagnetischen Feldes nur über die zweite Quantisierung
motiviert werden. Der Grundzustand des Systems, d. h. der Erwartungswert des
Vakuumzustands besitzt dabei die Energie:
|
|
(2.3) |
mit 
als Erzeuger und
als Vernichter im
abstrakten Zustandsraum (Hilbertraum) mit
zeitunabhängigen Zuständen, welche in der Mode 
ein zusätzliches Photon erzeugt bzw.
vernichtet und die Photonenzahl um 1 erhöht bzw. erniedrigt. Dabei wird das
atomare System durch den Erzeuger vom Grundzustand in einen angeregten Zustand
mit einer um 
erhöhten Energie überführt. Entsprechend regt
der Vernichter das atomare System ab auf einen neuen
Zustand mit einer um 
verminderten Energie:
|
|
(2.4) |
|
|
(2.5) |
Aufgrund
des zeitabhängigen optischen Feldes stellen sich Floquet-
Zustände ein und es müssen die zeitabhängigen Energiezustände des Atoms 
betrachtet
werden. Die zeitabhängigen Energien des Atoms können als Trajektorien im Phasenraum
beschrieben werden.
|
|
(2.6) |
In nicht- dissipativen Systemen bewegt
sich somit die Spur von 
auf der
Oberfläche von 
und macht 
konstant. Das bedeutet, das Potential ist
zeitlich konstant und die zeitunabhängige Schrödingergleichung
liefert uns die stationären Zustände 
und die
dazugehörigen Energien 
. Mithilfe der kanonischen Quantisierung
lässt sich in
Abhängigkeit der hermiteschen Operatoren 
und 
Energie in der
kanonischen Quantisierung schreiben:
|
|
(2.7) |
Dabei entspricht die Besetzungszahl der
Zahl der Photonen in der Mode des Feldes. Somit ist nichtzentrosymmetrische
Materie ein Hamilton´sches System. Die Form von 
für positive
Nichtlinearitäten 
bei kleinen
Energien ist ein einfaches Parabel- Potential, welches mit zunehmendem
Energieinhalt zunehmend asymmetrisch bezüglich der Potentialachse verläuft. Für
negative Nichtlinearitäten 
und 
besitzt das Potential eine an der
Potentialachse vertikal gespiegelte Form. Das Potential würde in nicht- dissipativen
Systemen mit zunehmendem Energieinhalt divergieren und Singularitäten bilden.
In realen Systemen ist dies ausgeschlossen.
2.2
NZS gebundene Elektronen in
dissipativer Umgebung
In realer Materie bewegen sich die
Elektronen der Schnittstellenatome in dissipativer Umgebung. Deshalb werden bei
unseren weiteren Potentialbetrachtungen dissipative Effekte durch Einführung
der Dämpfung mit 
berücksichtigt. Die
ungestörte Schnittstellen- Differentialgleichung für dissipative Systeme, d. h.
für 
kann geschrieben werden mit:
|
|
(2.8) |
Diese Form der Schnittstellengleichung
wird für die weiteren Betrachtungen, bei der Untersuchung
nichtzentrosymmetrischer Materie, als fundamentale Ausgangsgleichung herangezogen.
Für einen Dämpfungsterm ist das System dissipativ,
denn es resultiert in einer negativen Divergenz des Geschwindigkeitsfeldes.
|
|
(2.9) |
In dissipativer Umgebung mit 
bewegt sich die
Trajektorie von x auf der Oberfläche von , deren zeitliche Änderung von der Dämpfung abhängt und
proportional zu 
ist. Sie genügt der Beziehung:
|
|
(2.10) |
2.3
Lyapunov- Stabilitätstheorem
In dissipativen Systemen ergibt sich
die Situation, dass sich die Trajektorie von zwar auf der
Oberfläche von 
bewegt, aber dieses
nicht mehr konstant ist. Demnach verliert 
, in Abhängigkeit der Größe der Dissipation, mit der
Zeit an Energie, sodass abnimmt, solange
bis zum
Gleichgewichtszustand konvergiert wo, 
ist. Für 
und ist der einzige
Gleichgewichtszustand beim Fixpunkt 
, und 
erfüllt mit
|
|
(2.11) |
das Lyapunov-
Stabilitäts- Kriterium. Das heißt 
ist global
positiv definit und die Ableitung von 
ist global
negativ definit. Somit ist in diesem Fall 
eine Lyapunov Funktion und 
global
asymptotisch stabil. Auf der anderen Seite gibt es einen weiteren (labilen)
Fixpunkt auf dem negativen Peak. In diesem Fall werden die meisten Randbedingungen
zum Gleichgewichtszustand im Grundzustand konvergieren, in dissipativer
Umgebung wohlgemerkt. Ausgenommen sind die Randbedingungen, die der stabilen
Mannigfaltigkeit des Gleichgewichtszustands auf dem Peak entsprechen, d.h. die
diesen instabilen Fixpunkt stabilisieren.
|
|
|
|
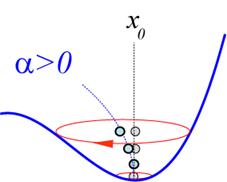
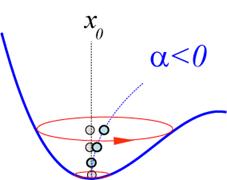
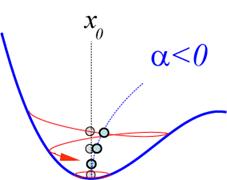
Abbildung
2‑2: Schematische
Darstellung des Energieverlaufs nichtzentrosymmetrischer Systeme in
Abhängigkeit der Nichtlinearität α mit eingezeichneter nichtdissipativer
Trajektorie im Phasenraum |
|
|
|
|
|
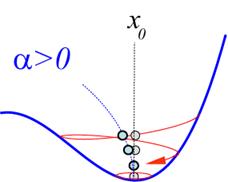
Abbildung
2‑3 zeigt den Energieverlauf
nichtzentrosymmetrischer Systeme in Abhängigkeit der Nichtlinearität α
mit eingezeichneter dissipativer Trajektorie (γ>0)
im Phasenraum |
|
2.4
Fixpunkte und deren Stabilität
Die obige Form der dissipativen,
störungsfreien Schnittstellengleichung, wird für die weiteren Betrachtungen bei
der Untersuchung nichtzentrosymmetrischer Materie als fundamentale Ausgangsgleichung
herangezogen. Das Gleichgewicht des Oszillators erhalten wir daraus durch
Substitution von 
|
|
(2.12) |
und somit gilt:
|
|
(2.13) |
Deshalb ist der Punkt
immer ein
Gleichgewichtspunkt. Zudem erscheint ein weiterer labiler Fixpunkt bei 
für positive Nichtlinearitäten und positiver
natürlicher Resonanz 
oder deren
jeweiligen Negation 
. Für den Si- Kristall erhält man mit 
eine labile Gleichgewichtslage im negativen Bereich
|
|
(2.14) |
Wir untersuchen jetzt das
Systemverhalten für kleine Amplitudenvariationen in der Umgebung dieser
Fixpunkte. Die Stabilität der gefundenen Fixpunkte kann mittels der
Untersuchung der Eigenwerte der Jakobi- Matrix verstanden werden. Die Jakobi
Matrix wird aus der rechten Seite der oben formulierten Schnittstellen- Differentialgleichung
für dissipative Systeme berechnet und lautet hierfür:
|
|
(2.15) |
Daraus ergeben sich die Eigenwerte für
den Gleichgewichtspunkt bei q =0 durch
|
|
(2.16) |
mit
|
|
(2.17) |
und
|
|
(2.18) |
Für den zentralen Fixpunkt 
lauten die zugehörigen
Eigenwerte:
|
|
(2.19) |
Daraus ergibt sich für μ ≠
0 ein instabiles Gleichgewicht für reelles μ und lineare Stabilität für
imaginäres μ. Die Hamilton´sche Struktur des
Systems erzeugt Stabilität aufgrund der linearen Stabilität. Dabei ist 
für 
. Wenn
aber 
wird, fallen die
beiden Wurzeln in (2.18) zusammen und der Fixpunkt wird instabil, d. h. ein Repellor liegt hier vor. Für 
und 
, d. h. 
erhalten wir einen
labilen Fixpunkt für die Imaginarität 
. Für
d. h. 
erhält man einen
stabilen Fixpunkt für reelles , d. h. die beiden Eigenwerte μ12
fallen zusammen, sodass dieser Punkt immer ein stabiles Zentrum, d. h. ein Attraktor sein muss. Als Ergebnis lässt sich eine
asymptotische stabile Gleichgewichtslage für hochgedämpfte Systeme für 
angeben und der
Fixpunkt ist ein stabiler Knoten. Der Fixpunkt wird instabil für schwach
gedämpfte Systeme 
und ist vom Typ stabiler
Strudel. Für negative Resonanzfrequenzen 
ergibt sich ein
Sattel. Für einen realen nichtzentrosymmetrischen Si-
Kristall erhält man die komplexen Eigenwerte 
. Für
den Si- Kristall erhält man instabile Fixpunkte. Der 2. Fixpunkt besitzt die Trajektoriekoordinaten 
mit den zugehörigen
Eigenwerten 
. Es ergibt sich daraus für und , d. h. 
ein instabiler Fixpunkt für imaginäres 
und für , d. h. 
ein stabiler
Fixpunkt für reelles , somit eine stabile Gleichgewichtslage. Für die
Fixpunkte 
erhält man Sattelpunkte. Den 3. Fixpunkt
erhält man für die Trajektoriekoordinaten 
mit den Eigenwerten 
. Dieser Fixpunkt ist wieder instabil für schwach
gedämpfte Systeme 
und der Fixpunkt
ist vom Typ stabiler Strudel. Für negative Resonanzfrequenzen ergibt sich ein
Sattel. Die Frequenz der kleinen Amplitude in der Umgebung des stabilen
Fixpunkts ergibt sich zu 
.
2.5
Diskussion und Zusammenfassung:
In diesem Abschnitt wurde detailliert das
Verhalten unbeleuchteter nichtzentrosymmetrisch gebundener Elektronen in dissipativer
und nicht- dissipativer Umgebung analysiert. Dazu wurde zunächst das
nichtlineare Potential nichtzentrosymmetrisch gebundener Elektronen analysiert.
Die zeitlichen Floquet- Zustände des Atoms werden
durch ein autonomes Hamilton- System in ein stationäres System entwickelt,
sodass die Energien des Atoms in nichtdissipativer Umgebung konstant werden und
somit auch das Potential konstant wird. Dabei wurde festgestellt, dass sich die
Spur der Trajektorien im Phasenraum auf der Oberfläche von bewegt und in
nicht dissipativer Umgebung 
konstant ist. In
dissipativen Systemen verliert diese Konstanz. Die
Lyapunov Stabilitätsuntersuchung liefert für positive
Nichtlinearitäten den einzigen Gleichgewichtszustand beim Fixpunkt als global
asymptotisch stabil. Für gilt das Lyapunov- Stabilitäts- Kriterium und sie ist eine Lyapunov Funktion. Es wurden drei spezielle Punkte des
Potentials nichtzentrosymmetrischer Materie durch die Analyse der entwickelten
Jacobi- Matrizen identifiziert. Die dazugehörigen stabilen Eigenwerte μ
konnten klassifiziert werden mit dem erzeugten analytischen Ausdruck
. Für μ ≠ 0 ergab sich ein instabiles
Gleichgewicht für reelles μ und lineare Stabilität für imaginäres μ. Die
Hamilton´sche Struktur des Systems erzeugt Stabilität
aufgrund der linearen Stabilität. Eine detaillierte Analyse der Umgebung der
erhaltenen Fixpunkte ergab, dass der zentrale Fixpunkt in Abhängigkeit von den
Parametern 
und 
stabilisiert
werden kann. Für 
wird der zentrale
Fixpunkt instabil, und es liegt ein Repellor vor. Für
erhält man ein
stabiles Zentrum in Form eines Attraktors. Als weiteres
Ergebnis lässt sich eine asymptotische stabile Gleichgewichtslage für
hochgedämpfte Systeme für 
angeben und der
Fixpunkt ist ein stabiler Knoten. Der zentrale Fixpunkt wird instabil für
schwach gedämpfte Systeme und er ist vom
Typ stabiler Strudel. Für negative Resonanzfrequenzen ergibt sich ein Sattel.
Der 2. Fixpunkt mit den Trajektoriekoordinaten 
ist für die Parameterrelation 
ein instabiler Fixpunkt für imaginäres 
und für 
ein stabiler
Fixpunkt für reelles , somit eine stabile Gleichgewichtslage. Für die
Realwerte des Si- Kristalls erhält man für die Fixpunkte mit 
Sattelpunkte. Den
3. Fixpunkt erhält man für die Trajektoriekoordinaten 
. Dieser Fixpunkt ist wieder instabil für schwach gedämpfte
Systeme und ist vom Typ
stabiler Strudel. Für negative Resonanzfrequenzen 
ergibt sich ein
Sattel.
