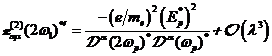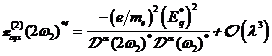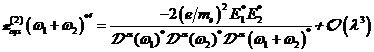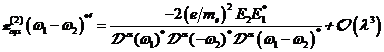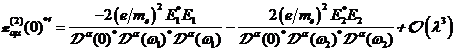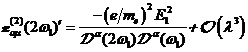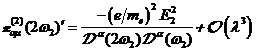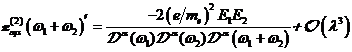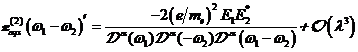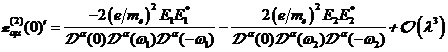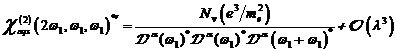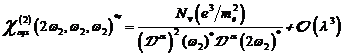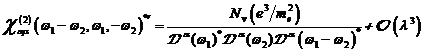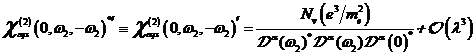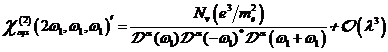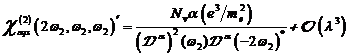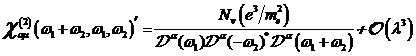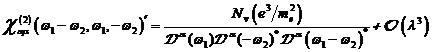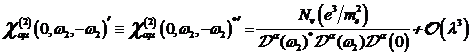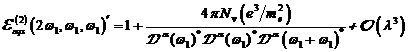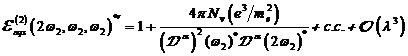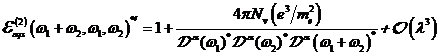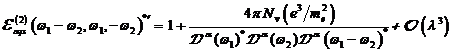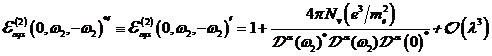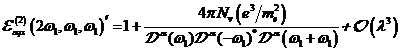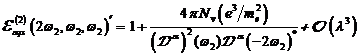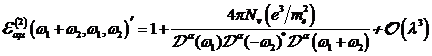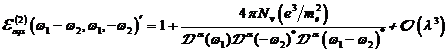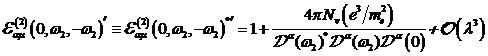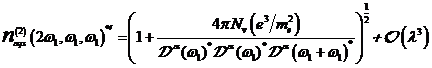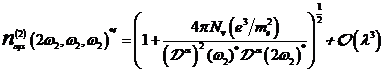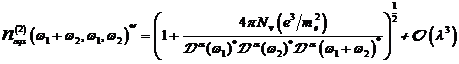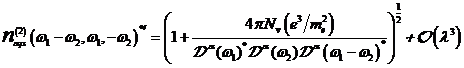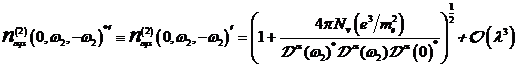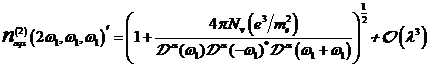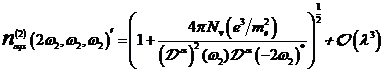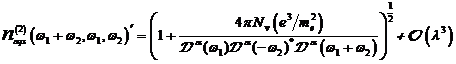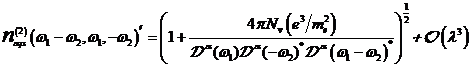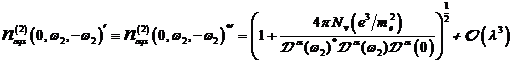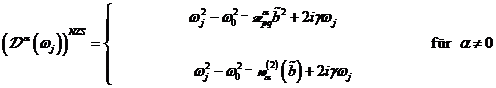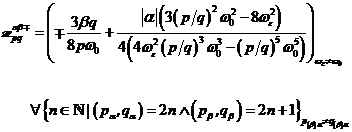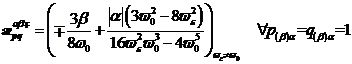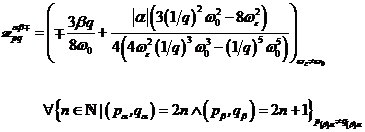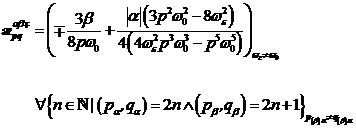Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie

Anhang A Ergebnisse

A.1: Makroskopische optische Response Tensoren

In diesem Abschnitt werden die Ergebnisse der Berechnungen aus den Kapiteln 4 bis 6 verzeichnet.

A.1.1: nichtlineare komplexe Fourieramplitude in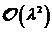

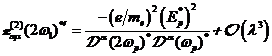
(A.1)

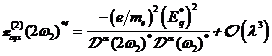
(A.2)

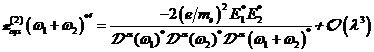
(A.3)

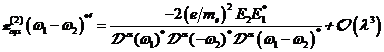
(A.4)

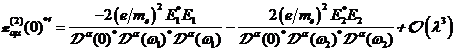
(A.5)

monochromatische c. c.- Felder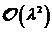

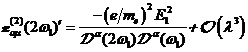
(A.6)

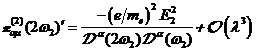
(A.7)

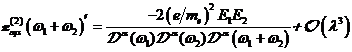
(A.8)

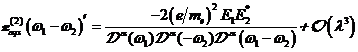
(A.9)

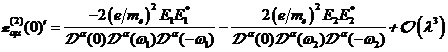
(A.10)

A.1.2: nichtlineare makroskopische Suszeptibilität in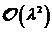

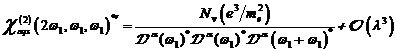
(A.11)

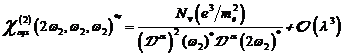
(A.12)

(A.13)

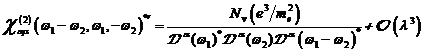
(A.14)

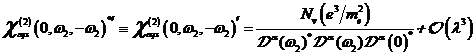
(A.15)

monochromatische c. c.- Felder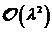

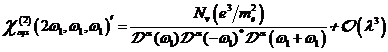
(A.16)

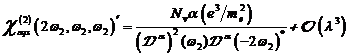
(A.17)

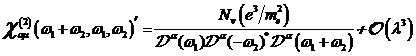
(A.18)

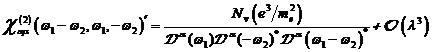
(A.19)

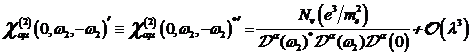
(A.20)

A.1.3: nichtlineare dielektrische Funktion in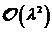

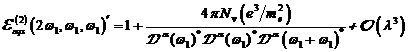
(A.21)

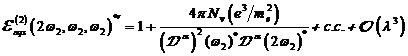
(A.22)

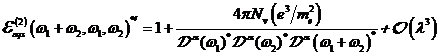
(A.23)

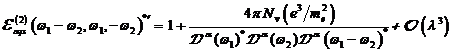
(A.24)

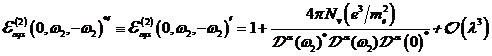
(A.25)

monochromatische c. c.- Felder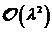

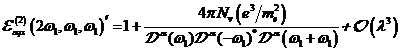
(A.26)

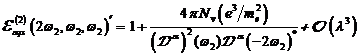
(A.27)

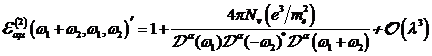
(A.28)

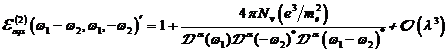
(A.29)

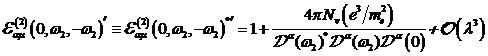
(A.30)

A.1.4: nichtlinearer makroskopischer Brechungsindex in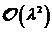

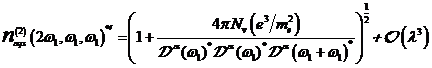
(A.31)

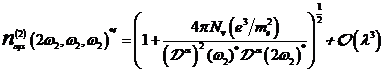
(A.32)

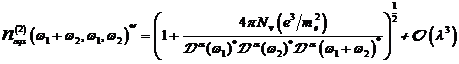
(A.33)

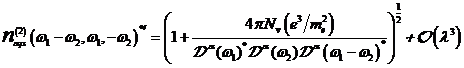
(A.34)

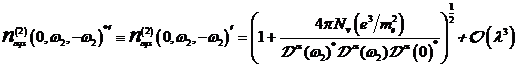
(A.35)

monochromatische c. c.- Felder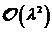

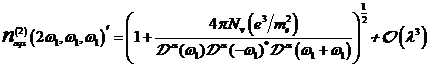
(A.36)

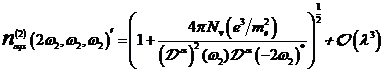
(A.37)

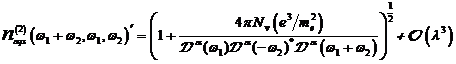
(A.38)

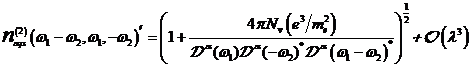
(A.39)

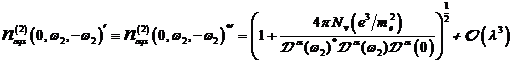
(A.40)

A.1.5: komplexe nichtlineare Resonanzfunktion für nichtzentrosymmetrische Materie in ,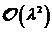

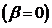
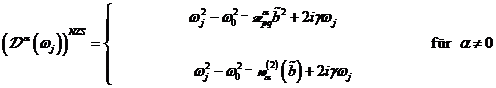
(A.41)

A.1.6: nichtlineare Koeffizienten in ,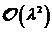

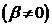
Allgemein

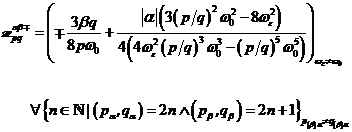
(A.42)

Fundamentale

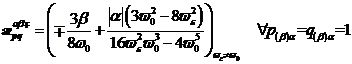
(A.43)

HHG,

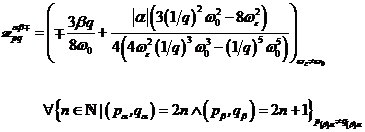
(A.44)

SubHG,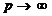

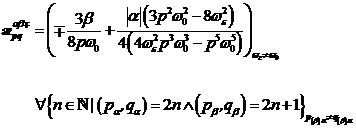
(A.45)

A.1.7: Simplified bond- hyperpolarizability model (SBHM)

(A.46)

Anhang B Programmentwicklung

B.1: Verzeichnis der Programm- Codes

Wie in den Kapiteln 3 und 4 beschrieben ist es möglich die zeitliche Entwicklung und die Fourierentwicklung des nichtlinearen optischen Responses mittels Computer- Physik zu behandeln. Die Codes der entsprechenden Mathematica^®- Programme sind hier verzeichnet.

B.1.1: Nichtlineare komplexe Fourieramplitude

Clear["Global`*"];

Off[General::spell1]

<<NumericalDifferentialEquationAnalysis`

<<DifferentialEquations`NDSolveUtilities`

SurfaceEquationNDSolve:=

{

x'[t]Šv[t],

v'[t]+2g v[t]+wres² x[t]+a x[t]²Š

-qspez ExternForce (Re[Exp[-ä wext t]]+Re[Exp[-ä 1/u wext t]])};

CRK4[___]["Step"[sigma_, t_, h_, y_, yp_]] :=Module[{k0,k1,k2,k3},

k0=h yp;

k1=h sigma[t+h/2,y+k0/2];

k2=h sigma[t+h/2,y+k1/2];

k3=h sigma[t+h,y+k2];

{h, (k0+2 k1+2 k2+k3)/6}

]

CRK4[___]["DifferenceOrder"] :=4

SurfaceNDSolve["{}"]:=

Block[{NDSolution,ListND,plotopts,initialConditions,param},

param ={wres=3.0386,wext=2.9786,g=0.013,

a=0.046165,qspez=2.920596161,

ExternForce=7.5,

tmin=0,tmax=500,u=1};

param;

initialConditions = {x0=0,v0=0};

initialConditions ;

SURFACESOLUTION[ wres_,wext_,g_,a_,qspez_,tmin_,tmax_,x0_,v0_,ExternForce_,u_,opts___]=

NDSolution:=

NDSolve[{SurfaceEquationNDSolve,

x[tmin]Šx0,

v[tmin]Šv0},

{x[t],v[t]},

{t,tmin,tmax},

Method®CRK4, Method®{"DoubleStep"},

StartingStepSize®1/10,

MaxSteps®Infinity];

xstart=x[tmax]/.NDSolution[[1]];

vstart=v[tmax]/.NDSolution[[1]];

ListND=Table[{

wext,FindMaximum [x[t]/.NDSolution,

{t,0.9tmax-2p/wext,0.9tmax}][[1]]},

{wext,0.1 wres,5.0 wres,0.001 wres}];

plotopts=

With[{optPlot = FilterOptions[ListPlot,opts] ,

optND =FilterOptions[NDSolve,opts]},

ListPlot[ListND,

Joined®False,

PlotRange®{{0.0,6.00},All},

PlotStyle®{PointSize[0.0043],Red},

ImageSize®{600,400},

AxesOrigin®{0.5,0},

AxesLabel®{"Frequenz w [1/fs]",

"Amplitude X(w)[pm]"},

Frame->True,

FrameStyle®{

{Directive[Thick,Black,16],

Automatic},

{Directive[Thick,Black,16],Automatic}},

GridLines®Automatic,

GridLinesStyle®Directive[Darker[Green],

Dashed]]]]

SurfaceNDSolve["{}"]

B.1.2: nichtlinearer Response in der Zeitdomäne

Clear["Global`*"];

Off[General::spell1]

<<NumericalDifferentialEquationAnalysis`

<<DifferentialEquations`NDSolveUtilities`

SurfaceNDSolution[ wres_,wext_,g_,a_,qspez_,tmin_,tmax_,ExternField_,u_]

Module[{NDSolution,NDList,InitialConditions},

InitialConditions = {x0=0,v0=0};

InitialConditions;

NDSolution=

NDSolve[{x'[t]Šv[t],v'[t]+2g v[t]+wres² x[t]+a x[t]²Š-qspez ExternField (Re[Exp[-ä wext t]]+Re[Exp[-ä 1/u wext t]]),x[tmin]Šx0,v[tmin]Šv0},{x[t], v[t]},{t,tmin,tmax},

Method®{"DoubleStep",

Method®{"ImplicitRungeKutta",

"Coefficients"->"ImplicitRungeKuttaGaussCoefficients",

"DifferenceOrder"®Automatic},

"ImplicitSolver"®

{"Newton",

"AccuracyGoal"®MachinePrecision,

"PrecisionGoal"®MachinePrecision,

"IterationSafetyFactor"®1/10 }};StartingStepSize®1/100,

MaxSteps®Infinity,

MaxStepSize®(1/10)];

NDList=x[t]

/. NDSolution;

Plot[NDList,{t,0,500},

PlotRange®All,

PlotStyle ® Hue[0.7],

PlotPoints®500,

ImageSize®{600,400},

AxesLabel®{"input frequency w","\nAmplitude A"},

PlotLabel®

Style["gedämpfte nichtlineare Response- Kurven 2. Ordnung"],

FrameLabel®{{"left label"},

{"bottom label"}},

PlotPoints®500,

Frame->True,

FrameStyle®{{Directive[Thick,Black,14],Automatic},

{Directive[Thick,Black,14],

Automatic}},

GridLines®{Automatic,Automatic},

GridLinesStyle®Directive[Darker[Green]]]]

ND=SurfaceNDSolution[

3.0386,2.9786,0.013,0.046165,2.920596161,0.,500,7,1

]

B.1.3: nichtlineare Trajektorie im Phasenraum

Clear["Global`*"];

Off[General::spell1]

<<NumericalDifferentialEquationAnalysis`

<<DifferentialEquations`NDSolveUtilities`

SurfaceSolution[ wres_,wext_,g_,a_,qspez_,tmin_,tmax_,E1_,u_,opts___] :=

Module[{NDSolution,InitialConditions},

InitialConditions = {x0=0,v0=0};

InitialConditions;

NDSolution=

NDSolve[

{

x'[t]Šv[t],

v'[t]+2g v[t]+wres² x[t]+a x[t]²Š

-E1*Re[ Exp[-ä wext t]]+Re[Exp[-ä 1/u wext t]],

x[tmin]Šx0,

v[tmin]Šv0},

{x, v},{t,tmin,tmax},

Method®{"DoubleStep",

Method®{"ImplicitRungeKutta",

"Coefficients"->"ImplicitRungeKuttaGaussCoefficients",

"DifferenceOrder"®Automatic}, "ImplicitSolver"®{"Newton",

"AccuracyGoal"®MachinePrecision,

"PrecisionGoal"®MachinePrecision,

"IterationSafetyFactor"®1/10 }};

StartingStepSize®1/100,

MaxSteps®Infinity,

MaxStepSize®(1/10)]

]

tmax=500;

SurfaceNDSol

=SurfaceSolution[

3.0386,2.7386,0.013,0.046165,2.920596161,0.,500,7.,1

];

ParametricPlot[

Evaluate[{x[t],x'[t]}

/.SurfaceNDSol],

{t,0.90*tmax, tmax},

AspectRatio®1,

PlotStyle ® Hue[0.0],

PlotRange®All,

PlotStyle®AbsoluteThickness[1.03],

ImageSize®{600,400},

PlotPoints®500,Frame->True,

FrameStyle®{{Directive[Thick,Black,16],

Automatic},

{Directive[Thick,Black,16],Automatic}}

]