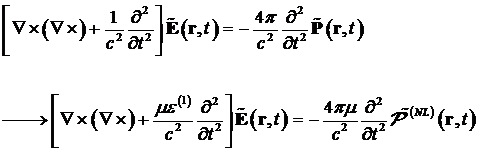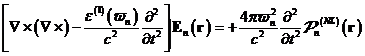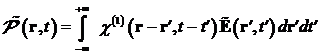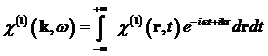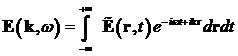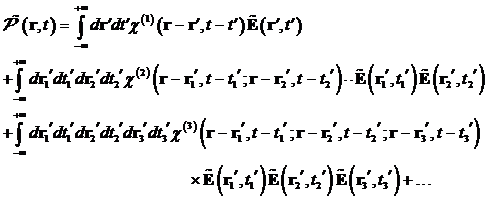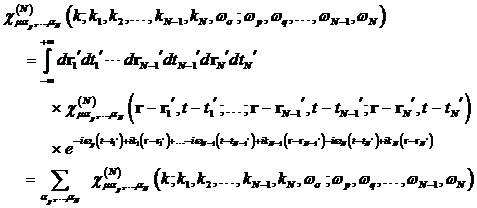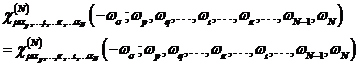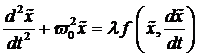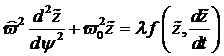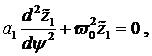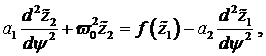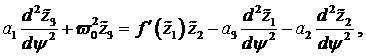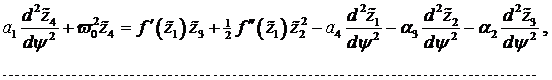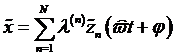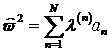Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie

Einleitung

Die in den letzten Jahren veröffentlichten theoretischen und experimentellen wissenschaftlichen Aufsätze [PA04, AHPPW03, PWA02, HPA03] haben uns veranlasst, das Verhalten von nichtzentrosymmetrisch gebundenen Elektronen im nichtlinearen Regime zu untersuchen. Diese sind in dieser Arbeit insbesondere die Generation höherer Harmonischer an nichtzentrosymmetrischer Materie. Der Bulk von Festkörpern ist zudem gut erforscht und in der Literatur dargestellt. Nichtzentrosymmetrische Medien dagegen sind simulationstechnisch sehr viel schwerer zugänglich und nur wenig erforscht. Bislang gibt es keine analytische Lösung der Bewegungsgleichung für nichtzentrosymmetrisch gebundene Oberflächenelektronen in Wechselwirkung mit bichromatischen photonischen Feldern. Dabei spielt sich die interessante Physik an der Oberfläche von Festkörpern ab, weil dort die zentrosymmetrische Bedingung verletzt ist, d. h. es findet keine Inversion aufgrund der Abwesenheit von Inversionssymmetrie statt.

In dieser Masterarbeit soll erstmals der genaue Mechanismus dieser speziellen Licht- Materie Wechselwirkung untersucht und eine exakte mathematische Modellbildung gefunden werden, welche auch für die Beschreibung organischer Systeme relevant wird. Nichtzentrosymmetrische Medien können Schnittstellen zwischen unterschiedlichen Materialien, sowie Flüssigkeiten oder Festkörperoberflächen sein. Wo es nötig war, wurden die Betrachtungen auf das Modell der kondensierten harten Materie kristalliner Festkörper konzentriert. Dabei beschäftigt sich die vorliegende Arbeit ausschließlich mit dem Elektronensystem, wobei die adiabatische Näherung von Born und Oppenheimer (1927) zugrunde gelegt wurde, in der das Elektronensystem und die Gitterdynamik der Atomkerne entkoppelt sind. In dieser Approximation ist die Bewegung der Atomkerne wegen ihrer 10⁴ bis 10⁵-fach größeren Masse sehr viel träger als die der Elektronen. Damit erscheinen für das Elektronensystem die dazu vergleichsweise langsamen Schwingungen der Atomkerne (Phononen) näherungsweise eingefroren zu sein, d. h. dem Atomkern können fixierte Koordinaten zugeordnet werden. Im Modell kondensierter Materie sind die meisten dieser Elektronen als Kern-Elektronen wegen der starken Coulomb-Anziehung fest an die Atomkerne gebunden. Sie bilden mit den Atomkernen eine Einheit, ein Ion. Zur Beschreibung der Valenz-Elektronen sind insbesondere ihre Dynamik und ihr energetischer Zustand wichtig. Ihre Beweglichkeit wird durch die kinetische Energie beschrieben. Sie bewegen sich nicht frei, sondern erfahren ein durch die Kern- Elektronen abgeschirmtes Coulomb-Potential der Atomkerne. Korrelationen zwischen den einzelnen Valenzelektronen werden vernachlässigt. Es verbleiben wenige bewegliche Valenz-elektronen, die jedoch aufgrund ihrer Beweglichkeit die elektrischen, magnetischen sowie einen Teil der thermodynamischen Eigenschaften der Festkörperoberfläche bestimmen. Zur Beschreibung dieser Systeme lassen sich störungstheoretische Analysen, wie die klassische Störungsrechnung, mit asymptotischen Näherungsverfahren sehr erfolgreich anwenden. In diesen Näherungen wird in den höheren Ordnungen eine genauere Beschreibung der einzelnen Valenz- Elektronen in nichtzentrosymmetrischer Materie erreicht.

Aufbau der Arbeit

Das Ziel der vorliegenden Arbeit ist eine analytische und numerische Untersuchung von nichtzentrosymmetrischer Materie in Wechselwirkung mit multichromatischen Photonenfeldern. Die Arbeit ist wie folgt gegliedert: Kapitel 1 rekapituliert die in dieser Arbeit verwendeten Methoden und Modelle zur Beschreibung höherer Harmonischer an nichtzentrosymmetrischer Materie, welches den derzeitigen Stand der Forschung wiedergibt. In Kapitel 2 wird die Hamilton´sche Struktur nichtzentrosymmetrisch gebundener Elektronen im nichtlinearen Potential erforscht, deren Ergebnisse zum Verständnis der darauffolgenden, im speziellen zum Verständnis der frequenzabhängigen Amplitude, wichtig sind. In den Kapiteln 3 bis 6 werden verschiedene Phänomene der Physik kondensierter harter Materie analysiert. Jedes dieser Kapitel kann unabhängig von den anderen gelesen werden und beginnt jeweils mit einer ausführlichen Einführung in die jeweilige Problemstellung. Das ist in den Kapiteln 3 und 4 die Frage nach dem exakten klassischen Mechanismus für den nichtlinearen Elektronenresponse in der Zeit- und Fourierdomäne. Es werden neue Ergebnisse für nichtlinear aktivierte und verstimmte Systeme vorgestellt. Bislang war abseits des einfachsten Modells dieser Art, in der linearen Approximation, wenig bekannt. Insbesondere werden dabei die Veränderungen mit wachsender Nichtlinearität für beliebige Ordnungen der Harmonischen und Subharmonischen erforscht. Im darauffolgenden Kapitel 5 werden mit diesen Erkenntnissen neue Ergebnisse für die makroskopischen optischen Response Tensoren erhalten, wobei Kapitel 6 mit der Betrachtungsweise des kollektiven Verhaltens nichtzentrosymmetrisch gebundener Elektronen im "Simplified bond- hyperpolarizability model" (SBHM), die Arbeit abschließt.

Kapitel 1

Methoden

1.1 Wellenaspekte nichtlinearer Optik

In diesem Abschnitt werden die Methoden und Modelle vorgestellt, wie sie in dieser Arbeit benützt wurden. Die Maxwell´schen Gleichungen, welche alle elektromagnetischen Phänomene beschreiben, sind etabliert und werden hier deshalb nicht explizit angeführt. Stattdessen konzentrieren wir uns auf die Wechselwirkung von Licht mit nicht- zentrosymmetrischer Materie. In isotropen, nichtmagnetischen (μ = 1), nichtlinearen Medien ohne freie äußere Ströme und Ladungen mit , in dem räumlich konstant ist, d. h. , können ebene Wellen als Lösungen der Wellengleichung angesetzt werden. Dabei ist im nichtlinearen Regime immer klein und für ebene Wellen kann es immer vernachlässigt werden. Mit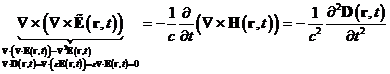

erhält man die Wellengleichung unter Ausblendung höherer Multipolmomente in Form der elektrischen Dipolmomentapproximation mit der Beziehung zwischen den Vektoren D, P und E:

(1.1)

wobei die Polarisation mit zusätzlich in einen nichtlinearen Teil aufspalten wurde. Mit dem Ansatz ebener Wellen in der Annahme dass mehrere Wellenlösungen unterschiedlicher Frequenzen existieren, mit , und

ergibt sich die Lösung der Wellengleichung zu

(1.2)

wobei die Frequenzkomponenten von D und E mit über eine frequenzabhängige dielektrische Funktion ε⁽¹⁾(ω) zusammenhängen, die im Falle von Verlusten auch komplex sein kann. Als Ergebnis erhält man eine Wellengleichung, in welcher die Polarisation mit dem nichtlinearen Response assoziiert wird, welches das elektrische Feld antreibt. Die nichtlineare Polarisation wirkt dabei als treibender Term für die elektromagnetische Welle der entsprechenden Frequenz. In der Wellengleichung treten keine räumlichen Abhängigkeiten auf. Im Allgemeinen ist die Polarisation eine Funktion der Zeit t und der räumlichen Koordinaten r. Jedoch im Modell der elektrischen Dipolnäherung ist das elektrische Feld gleichmäßig über das gesamte Molekül verteilt und die räumliche Abhängigkeit der Polarisation geht verloren, d. h. .

1.2 Approximierte Makroskopische Response Tensoren

Das Problem besteht jetzt darin, die nichtlineare Polarisation zu berechnen. Im linearen Fall ist die Polarisation verbunden mit dem externen optischen Feld durch die lineare Suszeptibilität in der Zeit- und Ortsdomäne gemäß:

(1.3)

Fouriertransformation der obigen Gleichung liefert, mithilfe des Faltungstheorems, Ausdrücke für die Raum- Zeitintegrale, in Form eines Produkts der jeweils Fouriertransformierten von und .

(1.4)

bzw.

(1.5)

mit

(1.6)

und

(1.7)

Mit den Maxwell- Gleichungen können wir in die lineare dielektrische Funktion konvertieren. Wir erhalten einen Tensor 2. Ordnung:

(1.8)

Für den allgemeinen Fall ist es möglich Gleichung (1.3) explizit in einen linearen Teil und in nichtlineare Teile aufzuspalten [SYR84]:

(1.9)

Wie zuvor kann Gleichung (1.9) fouriertransformiert werden und man erhält:

(1.10)

wobei die nichtlineare Suszeptibilität für den allgemeinen Fall ein Tensor (N+1)- ter Ordnung ist und von ω und k abhängt. Die Frequenzabhängigkeit ist implizit für den Rest dieser Arbeit wichtig.

(1.11)

mit als Tensorkomponenten der diskreten Superposition der nichtlinearen elektrischen Suszeptibilität N- ter Ordnung, mit den Fourierkomponenten , welche positiv, negativ oder 0 (resonante Frequenzen) sein können. Der Übergang zur diskreten Betrachtungsweise ist im Falle monochromatischer optischer Felder möglich. Die elektrische Suszeptibilität N- ter Ordnung charakterisiert die optischen Eigenschaften eines Mediums, welches darüber Auskunft gibt, wie das optische Material aufgrund des Feldresponses polarisiert wird. Die folgenden allgemeinen Beziehungen gelten für alle elektrischen Suszeptibilitäten:

(1.12)

Dies ergibt sich aus der Konsequenz reeller Felder. Unter Berücksichtigung des Energieerhaltungssatzes lässt sich anschreiben:

(1.13)

sofern nicht die Summenfrequenzerzeugung (SFG) gilt. Zudem ist die intrinsische Permutationssymmetrie gültig. Dabei können zwei Indizes permutiert werden, wenn gleichzeitig die dazugehörigen Frequenzen permutiert werden.

(1.14)

Mit der jetzt bekannten Suszeptibilität ist es möglich, den nichtlinearen Response N- ter Ordnung für jede Frequenzkombination des eingestrahlten optischen Feldes zu berechnen. In der lokalen Feldapproximation ist die Suszeptibilität unabhängig von r. Damit sind und unabhängig von k.

1.3 Ewald-Oseen Extinktions Theorem

Festkörperoberflächen kann man sich als eine Ansammlung von vielen ortsfesten polarisierbaren Atomen zusammengesetzt vorstellen. Das Ewald- Oseen- Extinktions- Theorem beschreibt die Reflexion von Licht an der Substratoberfläche auf atomarer Ebene durch diese strahlenden Dipole. Dabei erzeugt das optische Feld an der Festkörperoberfläche durch Polarisation der Atome ein ganzes Ensemble von Dipolen, deren emittierte Strahlung zum einen das optische Feld auslöscht und eine Polarisationswelle erzeugt, welches dem Snell´schen Gesetz gehorcht. Letztendlich wird dieses Licht mit den neuen Eigenschaften von der äußersten Dipolschicht vom Substrat emittiert. Dabei wird das abgestrahlte Licht zum reflektierten Strahl, wie in Abb. (1.1) anschaulich gezeigt wird. Von den beiden verbliebenen Beiträgen propagiert der Erste mit der Vakuumlichtgeschwindigkeit in den Raum und gehorcht der Wellengleichung für das Vakuum, wobei der einfallende Strahl vollständig absorbiert wird. Diesen Sachverhalt zeigte Ewald für diskrete Dipole [EPP16, EPP12] und Oseen für das Kontinuum [OCW15]. Der zweite Beitrag transmittiert mit verminderter Geschwindigkeit c/n durch das Medium und erfüllt das Snell´sche Gesetz. Weil die Intensität der erzeugten und der emittierten Strahlung in der gleichen Größenordnung liegen, müssen neben den emittierten Feldern auch deren Quellen berücksichtigt werden, weil sich diese zusätzlich auf die Antwort der Materie auswirken. Aufgrund der schwächeren Intensitäten der erzeugten höheren Harmonischen, welche zudem bei verschiedenen Frequenzen erscheinen, kann in der nichtlinearen Optik dieses schwierige Problem ausgeblendet werden. Dies stellt zur linearen Optik, entgegen der Intuition, eine erhebliche Vereinfachung bei der Behandlung nichtlinearer Systeme dar. Deshalb ist es möglich, die einzelnen Strahlungsbeiträge zu bestimmen und ihre individuellen kohärenten nichtlinearen optischen Beiträge durch Aufsummierung ihrer Felder im Fernfeld zu erhalten.

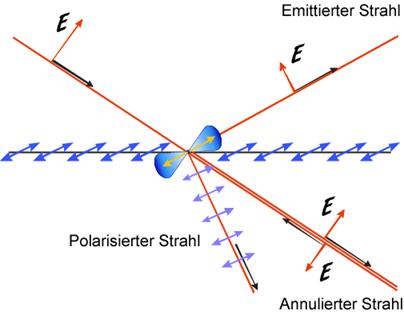
Abbildung 1‑1 zeigt schematisch das Ewald- Oseen Extinktions Theorem an nichtzentrosymmetrischer Materie. Die orientierten Oberflächendiplole sind entlang der Grenzlinie als blaue Doppelpfeile dargestellt.

Die typische Dimension dieser atomaren Dipol- Strahler liegen in der Größenordnung des 1. Bohr’schen Radius . Ihre typischerweise emittierte Strahlung liegt somit im sichtbaren Bereich. Mit Wellenlängen von Atomgrößen und Atomgrößen erhält man damit im Mittel Atomabmessungen, die in etwa um einen Faktor 10000 kleiner sind, als die Wellenlänge des optischen Lichtfeldes, mit dem das Atom wechselwirkt. Damit sind die elektrischen Dipolübergänge in Atomen dominant und viel intensiver gegenüber denen mit höheren Multipolfeldern.

1.4 Symmetriebetrachtungen in der makroskopischen Formulierung

Die nichtlineare Optik ist aufgrund ihrer höheren Ordnungssymmetrie von besonderem Interesse, die es erlaubt Oberflächen- und Bulkmaterial selektiv zu untersuchen. Aus diesem Grund ist die nichtlineare Optik im Bereich der spezifischen Oberflächen- Diagnostik sehr nützlich. Es bietet sich hier an, die makroskopischen Symmetrieregeln zu untersuchen, unter Berücksichtigung der Auswirkungen auf die Formulierung der nichtlinearen Optik. Die elektrische Suszeptibilität ist eine Eigenschaft des Materials und eine makroskopische Beschreibung ihrer elektronischen Struktur. In nicht- zentrosymmetrischer Materie sind nur gerade Ordnungen des nichtlinearen Responses erlaubt, wohingegen ungerade Ordnungen verboten sind, was hier kurz gezeigt werden soll. Zentrosymmetrische Systeme sind gegenüber einer Paritäts- Transformation ihrer kartesischen Koordinaten gemäß invariant, nichtzentrosymmetrische Systeme dagegen nicht. Wenn eine Paritätsoperation auf die Vektoren P und E ausgeführt werden soll mit ,, können die elektrischen Felder in den Richtungen und , indiziert mit angesetzt werden und man erhält eine resultierende Polarisation in - Richtung, wobei der Polarisations- Betrag für beide Richtungen gleich bleibt.

(1.15)

Für gerades N erhält man:

(1.16)

Der einzige Wert, welcher diese Gleichung erfüllt, ist . Dies beinhaltet, dass keine Polarisationen gerader Ordnung in zentrosymmetrischen Materialien beobachtet werden können. Deswegen ist unter Einbeziehung von Dipol verboten in zentrosymmetrischen Materialien. Ungerade Ordnungen dagegen sind nach Gleichung (1.15) unter einer Paritäts- Operation offensichtlich auch für alle Polarisationswerte ungleich Null erfüllt. Daher sind Harmonische gerader Ordnung in zentrosymmetrischer Materie Dipol verboten (zweite, vierte, ...), wohingegen die Generation ungerader Harmonischer (dritte, fünfte, ...) erlaubt sind.

1.5 Asymptotisches Näherungsverfahren nichtlinearer Systeme

In dieser Arbeit wir das Konzept der asymptotischen Näherungsverfahren nach [BM65] verwendet, welches hier auf das Problem nichtzentrosymmetrischer Materie angewandt wird. Das Randwertproblem, welches es dabei zu approximieren gilt, ist ein konservatives Schwingungssystem der Form:

(1.17)

Bei einem stationären Zustand ist die Amplitude konstant und ihre Ableitung folglich Null. Für eine beliebig genaue m- te Näherung erhält man für die Amplitude unveränderliche stationäre Werte b der Gestalt:

(1.18)

Um höhere Näherungen eines stationären Zustands zu erhalten wird die Lösung von (1.17) in der Form dargestellt, die eine periodische Funktion von mit der Periode 2 π ist. Die Amplitude erfüllt diese Gleichung wenn der Gleichung

(1.19)

genügt. Die Lösung (1.17) mit und erhält man in Gestalt der Reihenentwicklung

(1.20)

(1.21)

deren Koeffizienten, sich mit (1.20) und (1.21) substituiert in (1.19), aus den daraus folgenden Gleichungen bestimmen lassen. Dabei sind die 2 π periodische Funktionen von .

(1.22)

(1.23)

(1.24)

(1.25)

Mit den daraus bestimmten Funktionen und Größen lassen sich mit

(1.26)

die (N+1)- te Näherungslösung für stationäre Schwingungen von (1.17) bestimmen, wobei gilt:

(1.27)

Copyright © 2008, 2009, 2010, 2011 by Peter Krampl, www.mathematical-photonics.com. Die inhaltliche Zusammenstellung und Aufmachung dieser Publikation sowie die elektronische Verarbeitung sind urheberrechtlich geschützt. Jede Verwertung, die nicht ausdrücklich vom Urheberrechtsgesetz zugelassen ist, bedarf ausdrücklich der vorherigen, schriftlichen Zustimmung. Das gilt insbesondere für die Veröffentlichung, Vervielfältigung, die Bearbeitung und Einspeicherung und Verarbeitung in elektronische Systeme, jede Form der gewerblichen Nutzung, Nutzung als Grundlage für Lehrveranstaltungen, sowie die Weitergabe an Dritte - auch in Teilen oder in überarbeiteter Form. Das Copyright für hier veröffentlichte, vom Verfasser selbst erstellte Objekte bleibt allein beim Verfasser dieser Seiten.