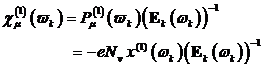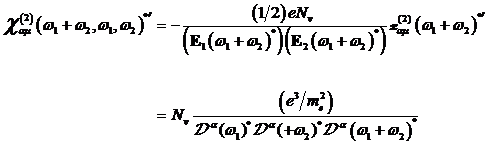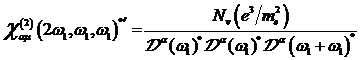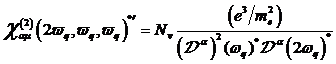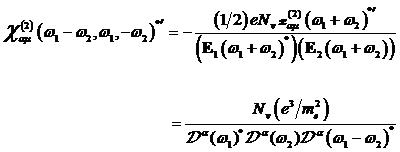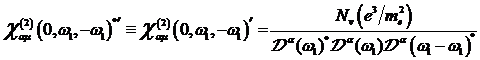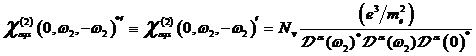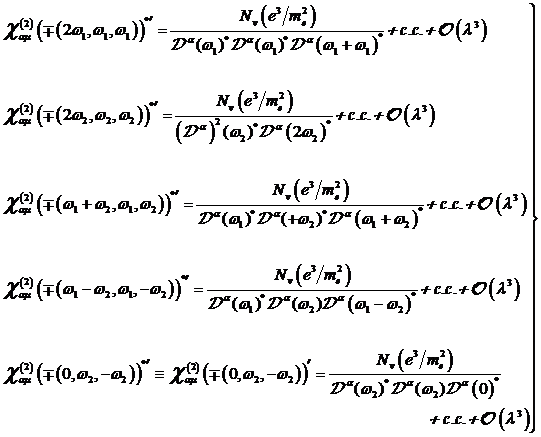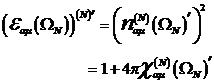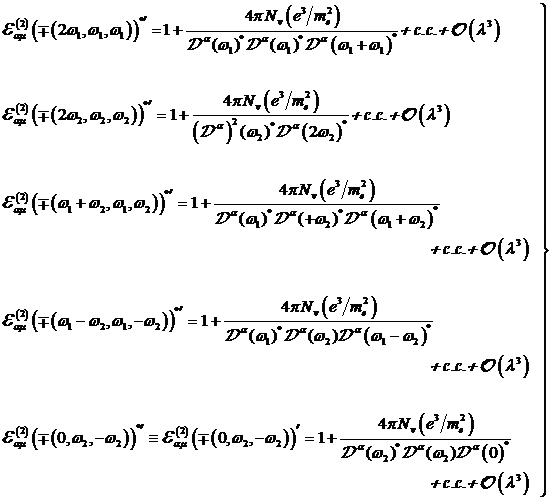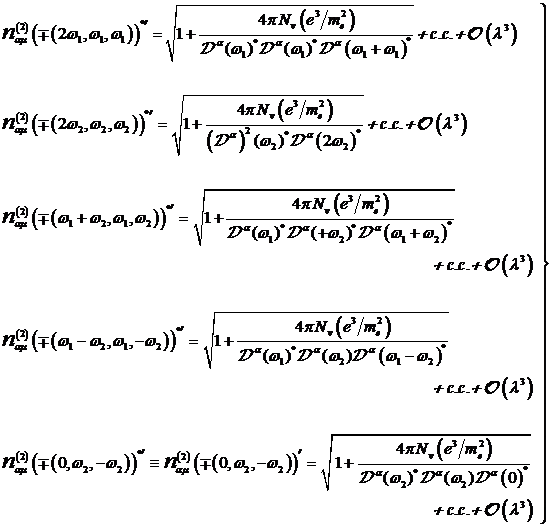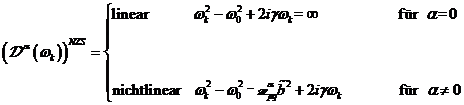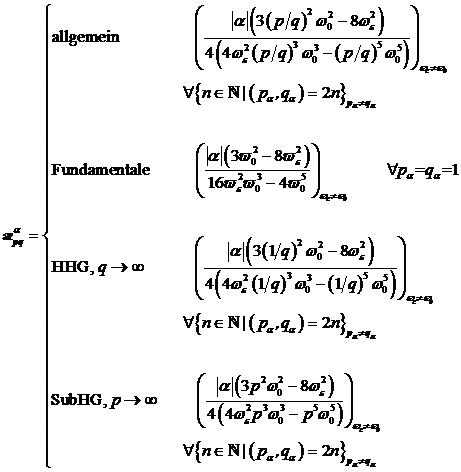Krampl, Peter: Komplexe Nichtlineare Optik - Theoretische Charakterisierung der 2- Photonen Resonanz nichtzentrosymmetrischer Materie

Kapitel 5

Nichtlineare Makroskopische Response Tensoren

5.1 Einführung

Im vorhergegangenen Kapitel konnte eine enorme Verbesserung der bisherigen Modellbildung erreicht werden, in der die Nichtlinearität in ihrem innersten Wesen exakt mathematisch modelliert wurde. Deshalb wird in diesem Abschnitt der nichtlineare Skewness- Effekt, wie er zuvor in Kapitel 4 dargestellt wurde, im Kontext der nichtlinearen Response- Tensoren diskutiert. Dazu wird vorrangig ein geeigneter Satz von neuen charakteristischen optischen Responsetensoren gesucht, welche nicht mehr rein lorentzartig sein können. Dies wird erreicht indem die nichtlineare Singularität in der störungstheoretischen Berechnung berücksichtigt wird. Dazu wird zunächst eine Übersicht über den klassischen Aufbau der nichtlinearen, optischen Response Tensoren nichtzentrosymmetrischer Materie präsentiert. Das sind die nichtlinearen elektrischen Suszeptibilitäts- und Dielektrizitätstensoren, welche die Materialeigenschaften beschreiben und wir führen dessen Notationen und Konventionen ein, wie sie in dieser Arbeit verwendet werden. Wenn nicht- zentrosymmetrische Systeme untersucht werden sollen, verschwinden nichtlineare Suszeptibilitäts- Tensoren in den Ordnungen mit , wobei Tensoren existieren, mit als erste von Null verschiedene nichtlineare Suszeptibilität. Daher werden wir unsere Diskussion hauptsächlich auf nichtlineare Tensoren in geraden Ordnungen konzentrieren.

5.2 Nichtlineare Suszeptibilität und Brechungsindex

Unter Berücksichtigung der hinzugewonnenen Erkenntnisse aus Kapitel 4 kann die nichtlineare Optik durch einen extrem kompakten Satz von neuen "exotischen" nichtlinearen, makroskopischen optischen Response Tensoren , und N- ter gerader Ordnung exakt analytisch beschrieben werden. Ausgehend vom dem Satz von Gleichungen (4.53), (4.55) und (4.56) lassen sich auch die nichtlinearen, optischen Response Tensoren für zentro- und nichtzentrosymmetrischer Materie exakt analytisch darstellen. Die lineare Suszeptibilität folgt trivialerweise aus dem linearen Polarisationsfeld mit

(5.1)

wobei die monochromatische Treiberfrequenz darstellt. Mit dem linearen c. c. Response der Gestalt ergibt sich für die lineare Suszeptibilität letztendlich

(5.2)

Die Beschreibung der nichtlinearen Suszeptibilitäten wird im Folgenden unter der störungstheoretischen Berücksichtigung der nichtlinearen Singularität für die Fourieramplituden ausgedrückt werden. Unter Zugrundelegung der Beziehung kann man die Polarisation im nichtlinearen Medium anschreiben gemäß:

(5.3)

Für die nichtlineare orbitale Suszeptibilität in der Näherung kleiner Größen in für die Summenfrequenzgeneration ergibt sich mit der komplex konjugierten Fourieramplitude in unter Berücksichtigung der nichtlinearen Singularität zu:

(5.4)

Dabei ist zu beachten, dass die Nichtlinearität im Zähler sich weghebt. Für monochromatische photonische Felder und erhält man die nichtlineare Suszeptibilität der komplex konjugierten 2. Harmonischen zu

(5.5)

und

(5.6)

Analog zur mathematischen Modellierung von SFG erhält man die Ausdrücke für die Fourieramplitude für DFG für den negativen Differenzfrequenzbereich zu:

(5.7)

wobei die lineare c. c. Fourieramplitude in der Näherung kleiner Größen , mit zugrundegelegt wurde. Für identische Frequenzen bzw. ergibt sich daraus der komplex konjugierte (c. c.) Gleichanteil der nichtlinearen Suszeptibilität zu:

(5.8)

und

(5.9)

Insgesamt erhält man hiermit weitere zwei Formelsätze von neuen "exotischen" Ausdrücken zur Beschreibung der Wechselwirkung von bichromatischen Photonenfeldern mit nichtzentrosymmetrischer Materie. Die nichtlineare Suszeptibilität in besitzt für komplex konjugierte Felder behobene Singularitäten bei den Resonanzen mit den Frequenzen -2ω₁, -2ω₂, -(ω₁+ω₂), -(ω₁−ω₂), welche jetzt einen amplitudenabhängigen negativen Skew aufweisen.

(5.10)

Die nichtlineare Suszeptibilität in setzt sich also aus der Summe all dieser Komponenten zusammen. Dabei ist zu beachten, dass die Nichtlinearität α als Proportionalitätsfaktor in diese Gleichungen mit eingeht, in der die Amplitude direkt linear beeinflusst wird. Dabei charakterisieren die Materialeigenschaften mit die Plasmafrequenz. Im letzten Teil dieses Abschnitts liegt das Hauptaugenmerk auf die neu zu formulierenden Spektraleigenschaften der nichtlinearen Antwort nichtzentrosymmetrischer Materie auf monochromatische Felder und gibt die molekularen nichtlinearen Tensoren im Fourier- Raum zusammenfassend an. Mithilfe der Dispersionstheorie lässt sich auf den exakten molekularen Dielektrizitätstensor beliebiger Ordnung schließen und somit der nichtlineare Brechungsindex exakt analytisch bestimmen. Für homogene, isotrope Materie kann man anschreiben:

(5.11)

wobei die optischen Pumpfrequenzen darstellen. Für bichromatische c. c. Photonenfelder und deren komplex konjugierten Felder erhält man damit:

(5.12)

bzw. für den nichtlinearen Brechungsindex

(5.13)

wobei die komplexe nichtlineare Resonanzfunktion unter Berücksichtigung der Singularitätslinie nichtzentrosymmetrischer Materie allgemein angeschrieben werden kann

(5.14)

mit den Anharmonizitätskoeffizienten, , welche allgemein die Skewness für Harmonische und Subharmonische beliebiger Ordnung mit einer Genauigkeit berücksichtigt.

(5.15)

5.3 Diskussion und Zusammenfassung:

In diesem Abschnitt wurde ein geeigneter Satz von neuen charakteristischen optischen Responsefunktionen, welche unter Berücksichtigung der neu hinzugewonnenen Erkenntnisse nicht mehr lorentzartig sind, für nichtzentrosymmetrische Medien motiviert und dessen Wichtigkeit für die verschiedenen nichtlinearen orbitalen Response Tensoren gezeigt. Mit den gewonnenen Erkenntnissen ist es jetzt möglich, die nichtlineare Optik durch einen extrem kompakten Satz von nichtlinearen, makroskopischen optischen Response Tensoren , und N- ter gerader Ordnung exakt analytisch darzustellen. Die Betrachtungsweisen, wie sie in dieser Arbeit vorgenommen wurden, können analog für jegliche lineare und nichtlineare Materie und in jeder beliebigen Kombination davon angewandt werden.