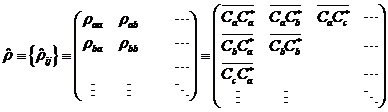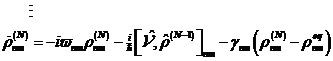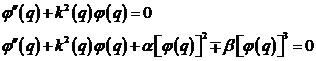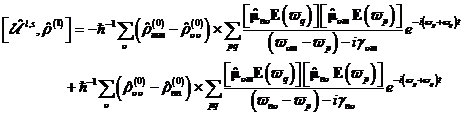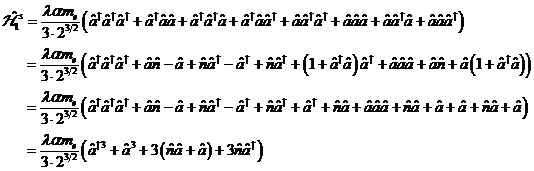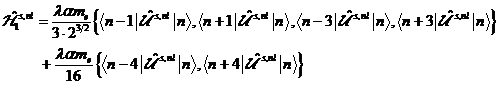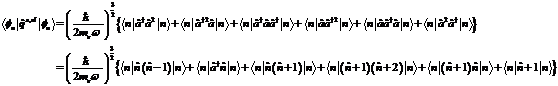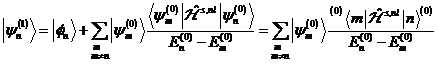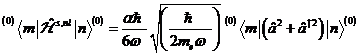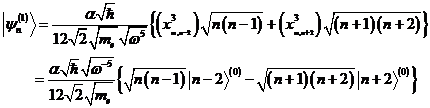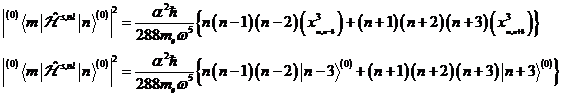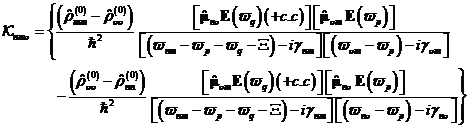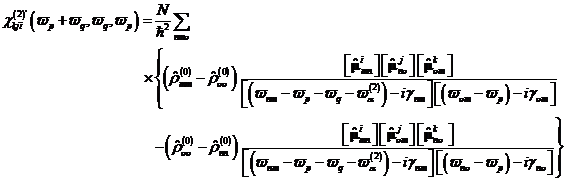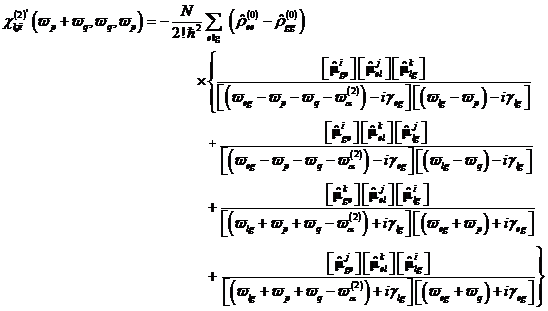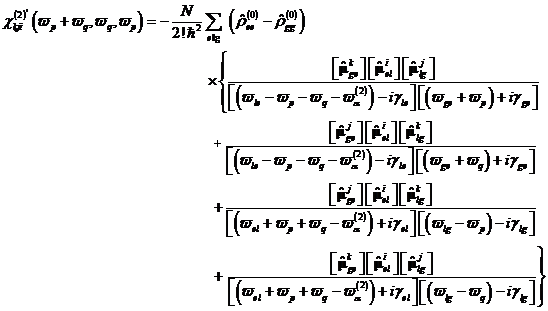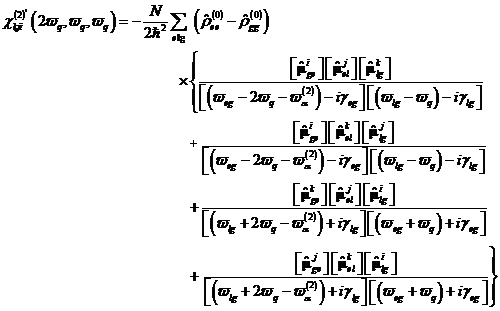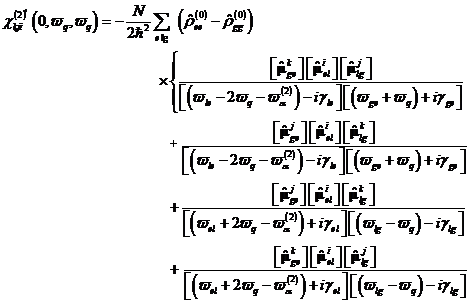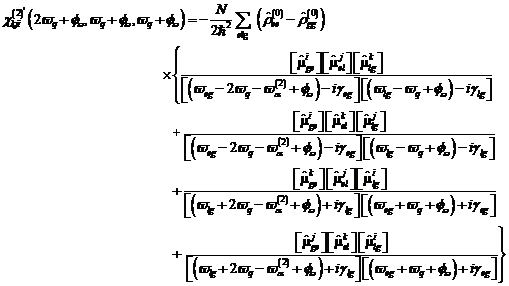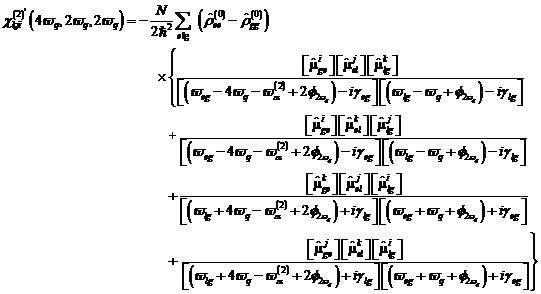| Peter Krampl
Complex Nonlinear Quantum Systems:
Nonlinear Quantum
Photonics in dependence of the matter symmetry |
HOME
   |
Chapter 1
1
Methods
1.1
Density matrix formalism in the Schrödinger picture
The system dynamics is described now in detail by means of
density matrix formalism. Subsequently
some basic drafts
are represented to that. In that the state of the system is described
through the density operator - a member
of the class of positive operators (C*
algebra) in the hilbert
space that is united with that with the system. Suitably
this density operator is defined in
the configuration
room:
|
|
(1) |
While the state of the system is
being defined through the density operator,
their dynamics is described through a superoperator which
operators shows in the hilbert-
space into other operators. This
construction defines a
hilbert-
space the vectors operators are in which one and the dot product
is declared through
|
|
(2) |
United to Observablen that one are with a hermiteschen operator on the
hilbert
space of the system are defined
according to:
|
|
(3) |
The precise states are not more
known due to the interaction between the atoms. In
this
case the density matrix formalism can be
used in order to describe the system statistically.
|
|
(4) |
at what the quantity
the probability in more classical and to interpret not in quantum
mechanical respect is, with which the system is in the s state. In this way p(s) reflects our
knowledge gap about the
current quantum mechanical state of the system, at which it is no consequence
of the sort of the quantum mechanical uncertainty relation represents. Moreover
is
the probability amplitude (
=
hermitesch to) and
as an average about all possible ensemble
states with m, n as indexes about all Energieeigenzustaende of the ensemble. On this discrete Hilbert
space the
density operator is represented as
a matrix: In the ourierdiskretisierungsschema becomes
represented with:
|
|
(5) |
The diagonal
elements of the matrix
are at that always real and the populations of the Energieeigenzustaende set
dar, during the complex nondiagonal elements
to represent the coherence between the states n and m, in the
assumption that
is, if the system is in a coherent overlay
with the n energy intrinsic values and with
far the nondiagonal elements are, under certain circumstances, proportional to the
induced electrical dipole moment of the atom. Under coupling of the
density operator with the
time-dependent Schrödinger
equation of the wave function
one reaches for the movement
equation for the density matrix, the so-called Liouville
equation or of new man equation in
the Schrödinger
picture:
|
|
(6) |
with
as Wechselwirkungshamilton,
as a density matrix operator in the
Schrödinger
picture. In this
case the commutator became from
and with the development
in
transfer. The dissipative
surroundings become sufficient through the introduced phenomenological
damping term
considers, which the relaxation of
into the basic state
with the disintegration rate
caused.
|
|
(7) |
With the vacuum-theory the longitudinal and transversal relaxation can be written
with:
|
|
(8) |
|
|
(9) |
1.2
Kinetics
of the
density matrix
In this section the non-linear molecular
hyperpolarization is determined about the
density matrix with the aid of the
constructed non-linear potential. For this purpose the Liouville
equation is
supposed to be considered. This delivers for the array
elements
a system of coupled differential equations for
which there is not any solution in analytically closed form. It is, however,
possible to search a solution with the aid of the quantum mechanical
Rayleigh- Schrödinger
perturbation
theory that distributes the solution of the eigenvalue
equation as a function of the λ parameter. For this
purpose the trouble becomes
with
in variable form applied:
|
|
(10) |
For
the system is
in the thermodynamic balance. Substitutes into those of new man equation in the
perturbation theory of first order successive
approximations for those ones delivers
to the form.
|
|
(11) |
With
and
we receive the
analytical expressions N-
th order.
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
That (first
equation) describes the time development
of the system in the absence of some external optical field. We
receive the stationary solution with
, at what
. To the solution of the non-linear quantum-optical
problem the subsequently formulated non-linear eigenvalue equation is to be solved
|
|
(17) |
and/or
considering the heat losses of a dissipative orbital
resonance interaction with photons
|
|
(18) |
at what valid is:
|
|
(19) |
that
is k now a regular energy spectrum, a discrete in quantum
systems, contains. The exact molecular Hyperolarizability and Suszeptibility can be determined about the
density matrix. This procedure is
easily applicable on any high orders. The density matrix in the case of the
2nd order on the basis of the atomic one 3- level
system's with the states |g >, |l >, |e > we can write:
|
|
(20) |
for monochromatic photonic fields
we choose
;
and none
activated find non-linear effects:
|
|
(21) |
At that the characteristic of a linear system, there a single field flooded in, turns out regardless as strongly it can interacting with the atom, not activated any non-linear effects. For this purpose a second separate field is urgently necessary. In the case of multiphoton ionization with more than a photon we receive non-linear effects which through following integral developed is considered in shape of.
|
|
(22) |
In order the
activated non-linearity processes
we must consider the atomic system considering the effective non-linear
potential formulate. For this purpose the non-linear Hamilton
operator of the form becomes
with a within a
given time periodic trouble of the form
take as a
basisly. The correction of the non-linear energy intrinsic values of not
degenerated levels of arbitrary order occurs wi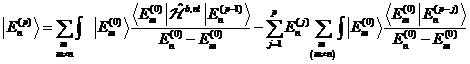th
with
, at what levels' not degenerated for the
calculation of the non-linear correction of the state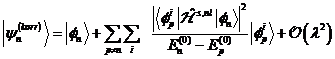
is taken as a
basis. Considering the sturgeon term with
with
when destruction- and
as a production operator the non-linear
Hamilton operator for
centro- and
noncentrosymmetrical matter
makes itself chalk up according to with the aid of the commutator theory:
|
|
(23) |
and
|
|
(24) |
with
|
|
(25) |
at
what the Commutator relation
,
,
people were useful. The correction of the
non-linear energy intrinsic
values of not degenerated levels in second order occurs by means of non-linear Hamilton operator
|
|
(26) |
and
to non-linear orbital deformation
|
|
(27) |
With
the distribution taken as a basis
a disappearing
correction turns out due to the commutator symmetry in first approximation for surfaces. Thus none surrender
Energy- and also no state corrections for surfaces in the approximation of small sizes of first order because is valid:
|
|
(28) |
with
|
|
(29) |
follow
furthermore
|
|
(30) |
|
|
(31) |
The
energy correction for
noncentrosymmetrical matter submits in this way to 2nd approximation of small
sizes too:
|
|
(32) |
Integration considering two fourier components delivers
|
|
(33) |
with
|
|
(34) |
at what in dependence of their crystal symmetry is valid:
This model
formation considers the necessary demand that first through multiphoton
ionization under participation of at least 2 photons a correction turns out and
non-linear effects are activated by that. With distinguishing the matter
answers produced in that at the surface from those of the Bulk selectively possibly
what up to now was not possible it is. In this way the
thick one lets itself to the exact non-linear molecular susceptibility
of 2nd order of the sum frequency production and difference frequency
production in analytical form to an ensemble of independent molecules N
in dipole approximation,
in simple way with the own functions < m| and the corresponding
intrinsic
values Em estimate and with Feynman- slide grams graphic
represent. A three-stage atomic AtomSystem describes the result in this formulation
about all population differences of the states m and n above ν for the non-linear susceptibility in dissipativer
surroundings.
|
|
(35) |
Around
the complete terms to preserved a summation is carried out at that
about all states (Couplings, initial values) and the intrinsische permutation symmetry
considers. For the case of different insolation
frequencies
we receive with
the antiresonant contributions of 4 terms the / for the sum frequency production (SFG) and 4 terms of the frequency variation production (DFG).
|
|
(36) |
|
|
(37) |
The
analytical expressions for the Suspzeptibilitaet are let to state system in that 3 interpret. Only the energy states a, b and c
interacting noticeably with the optical field. The created field with the
frequency ϖ1 is near the resonance, the crossing a b.→ The created
field with the frequency ϖ2 is near the resonance of the
crossing b c→
and the generated field frequency ϖϖ3 = ϖ1 + 2
is near the resonance of the crossing c a.→ The generated intensity is the more intensely better the resonant denominator
functions with the atomic states agree.
We receive summation terms over the populations. The terms become in this case
/ squeezed out in dependence of the populations, and consider at that that only
the basic state
is filled that is.
with
as the valence
of the basic state l,
the
array element the in-
components ten of the dipole operator between the
n states and m,
that an energetic distance of
have. The
coherence between the two states falls apart with the phenomenological damping
constants
. For the special case of identical optical insolation frequencies
let's receive the expressions for the frequency
multiplications and the optical dc component DC. For SHG and DC we receive the analytical expressions in dependence of the
population differences:
|
|
(38) |
|
|
(39) |
what
the antiresonant contributions were considered additionally at. These
analytical expressions do not show any resonant crossing, but they fall apart
into the basic state. This can be interpreted in the
means as fluctuations around the
basic
state. For photo and spin currents also
analytical expressions can be formulated in this way. One recognizes that for certain phase detuning the quantum states can be found
exactly and so maximum population and coherence of the underlying quantum systems shows.
|
|
(40) |
|
|
(41) |
with
as non-linear
corrections according to the developed non-linear theory in dependence of
their symmetry and load
structure, electron and holon. In this case become
for dephasing according to
Photocurrents generates
and for
dephasing with
maximum load
streams produced.
In this way we receive DFDs of the form:
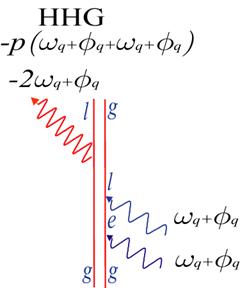
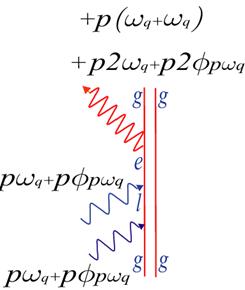
For
two state-systems
only these two crossings are programmable. For higher frequency crossings and/or Photo- and Spincurrents must be
introduced further transition.