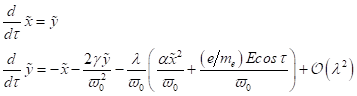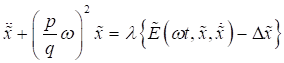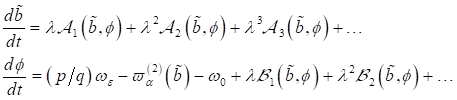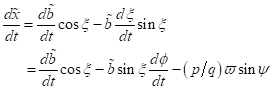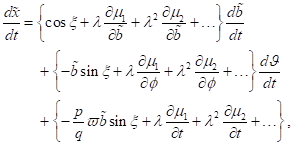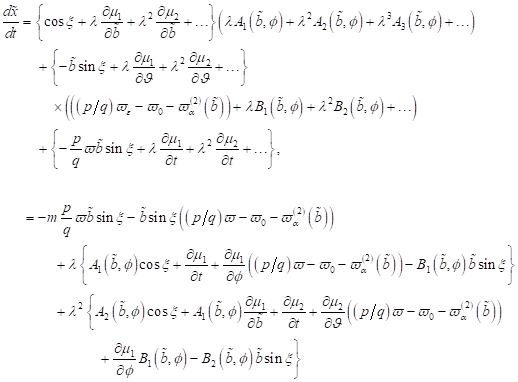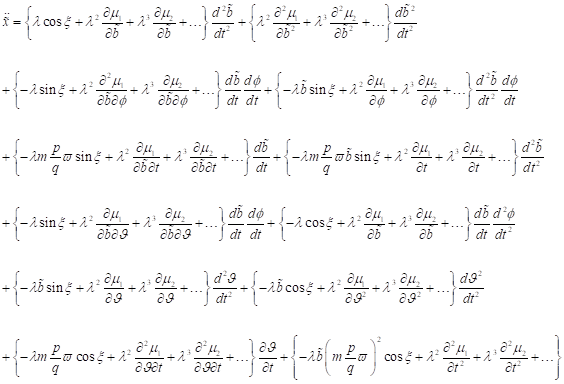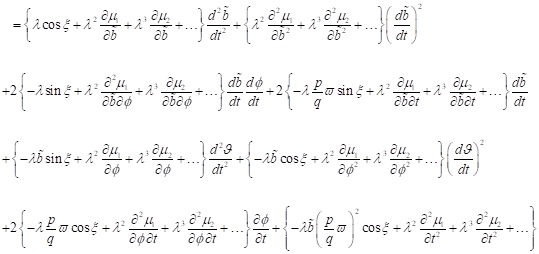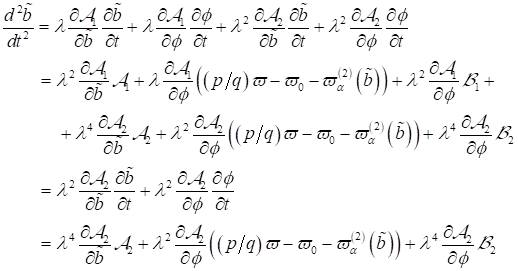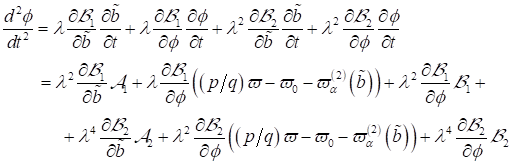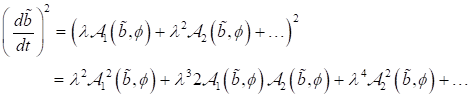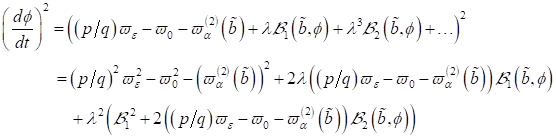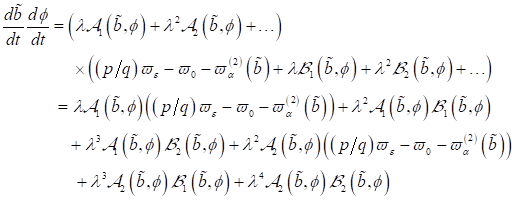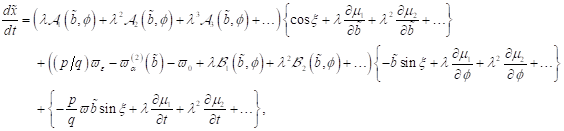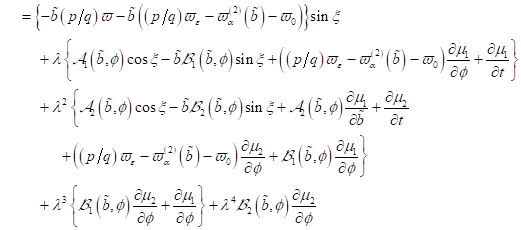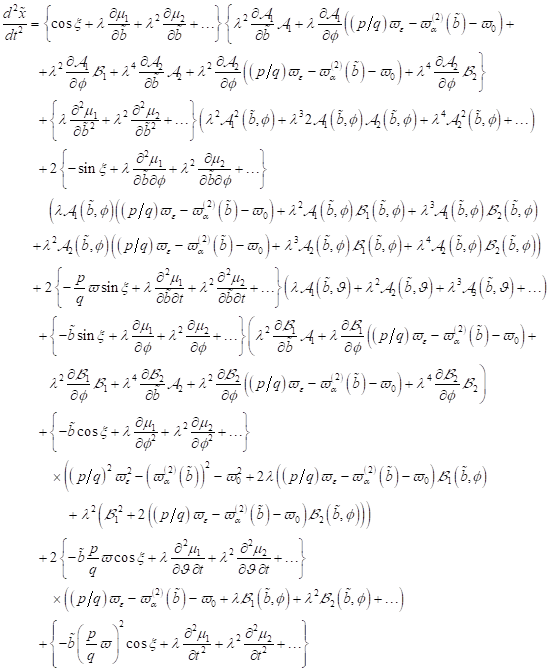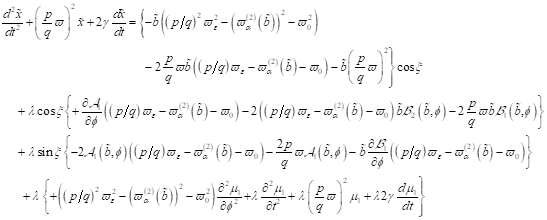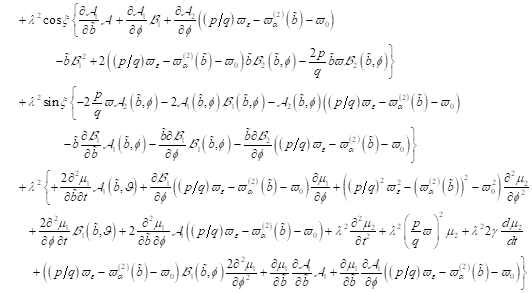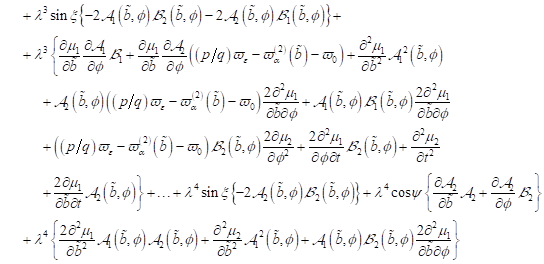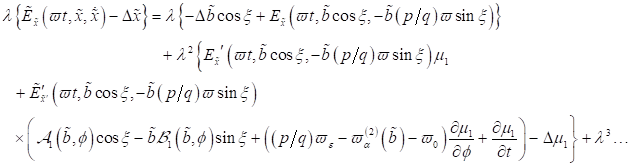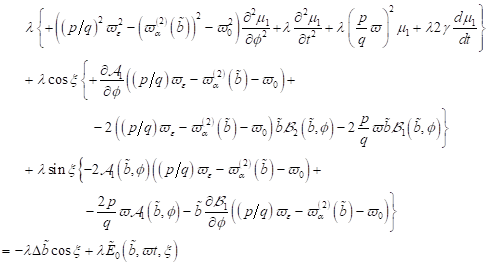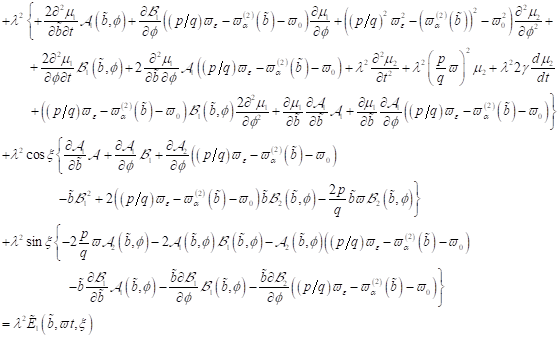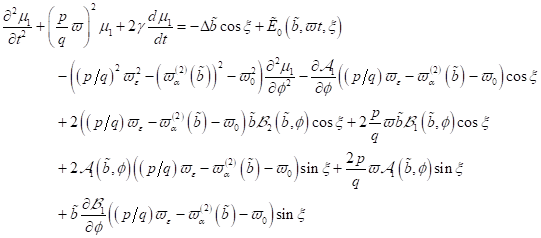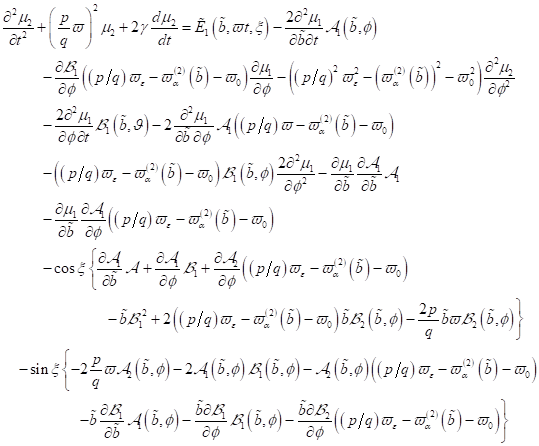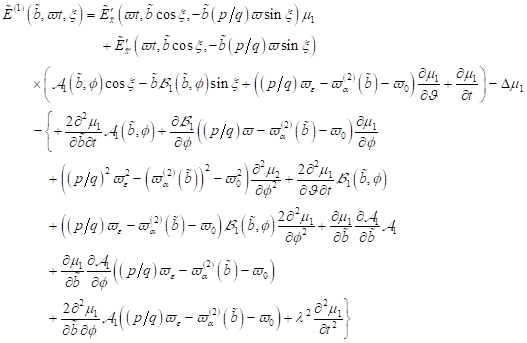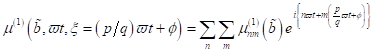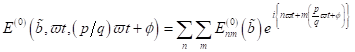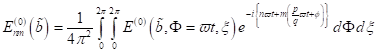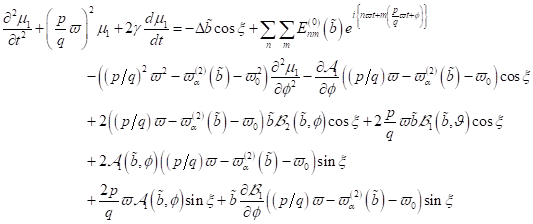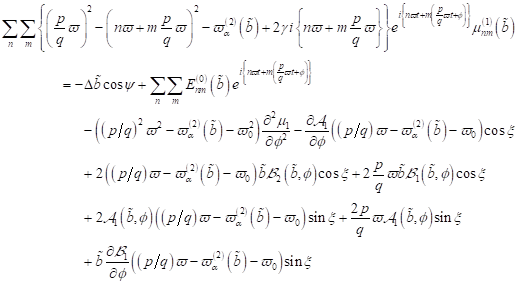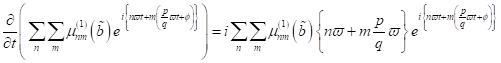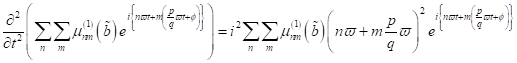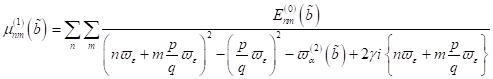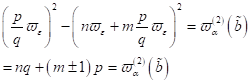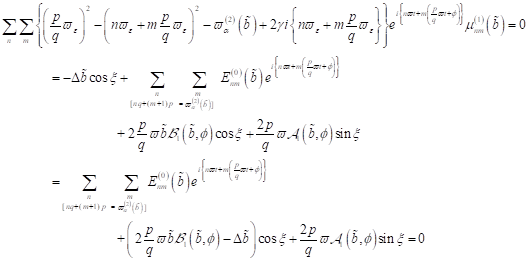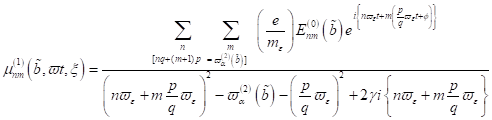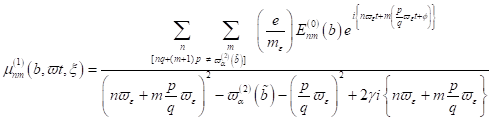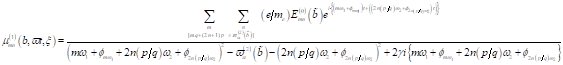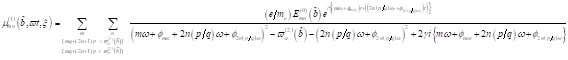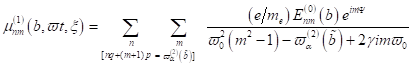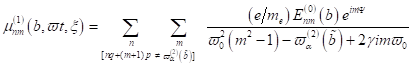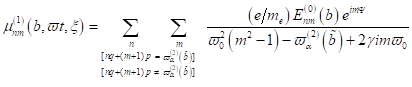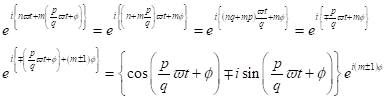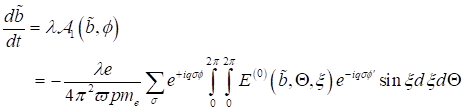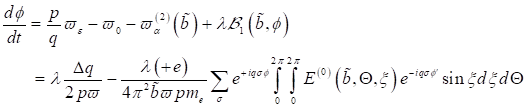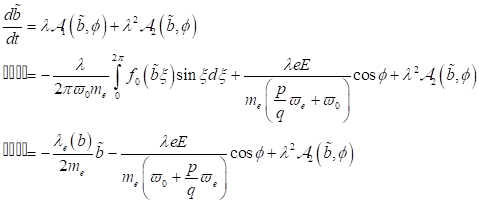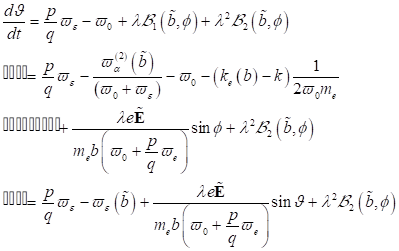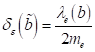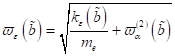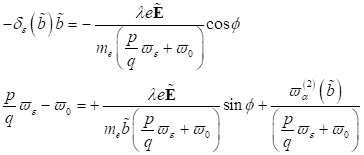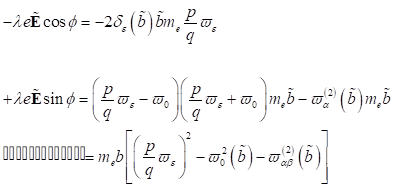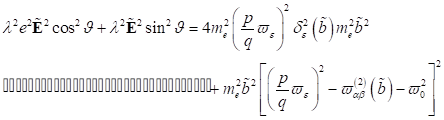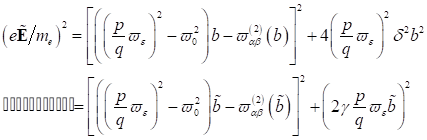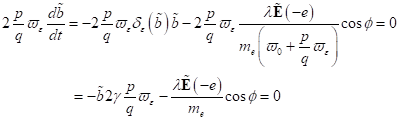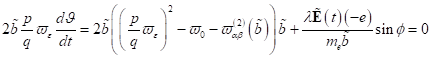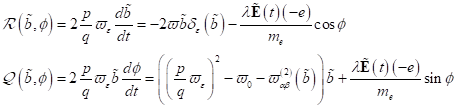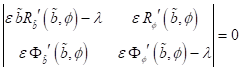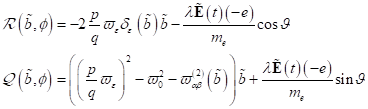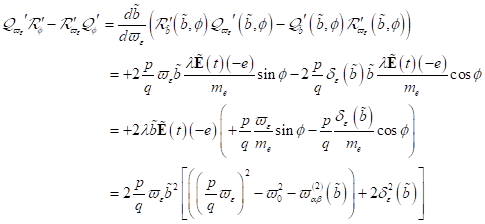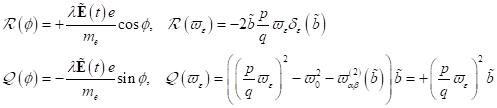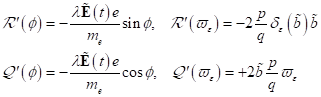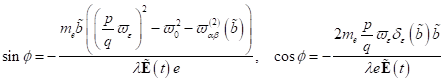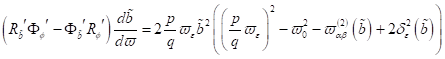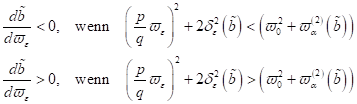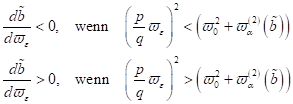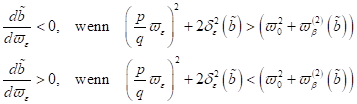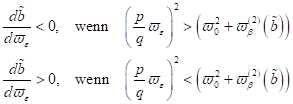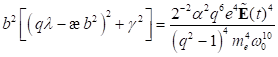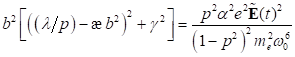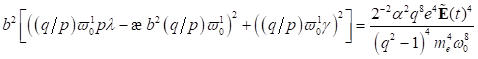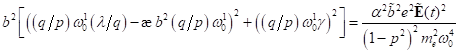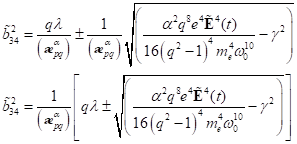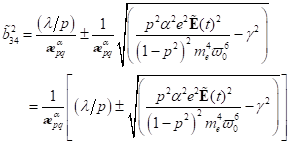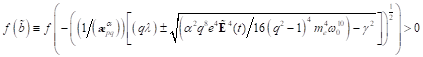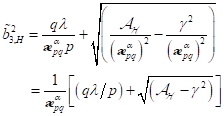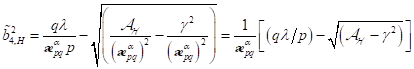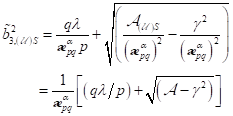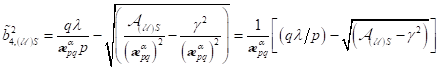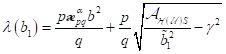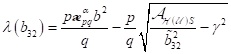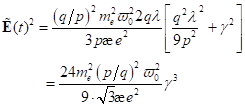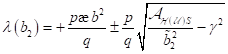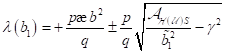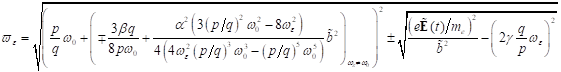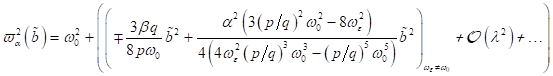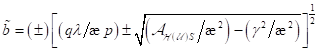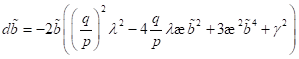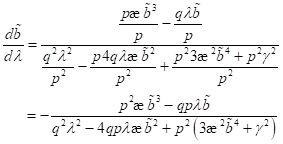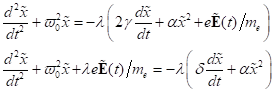Nichtlineare Singularitäten und
Bifurkationen
P. Krampl*
1. Zusammenfassung: In dieser
Arbeit wurde detailliert das Verhalten unbeleuchteter nichtzentrosymmetrisch
gebundener Elektronen in dissipativer und nicht- dissipativer Umgebung
analysiert und der Fall zentrosymmetrischer Materie mit berücksichtigt. Der
genaue Mechanismus der Generation und Kinetik von Photo- und Spinströmen an
Oberflächen und tieferliegenden Bulkbindungen wurde detailliert untersucht und
eine neue Modellbildung entwickelt. Die Untersuchung der zeitlichen Entwicklung
der Elektronen- Trajektorie im Phasenraum zeigte weit unterhalb des
Bifurkationspunktes für negative als auch positive Verstimmungswerte eine
Kreisbahn, welche mit sukzessiver Annäherung an den Bifurkationswert deutlich
von Spiral- und Kreisbahnen abweicht. Der Grad der Verstimmung bestimmt die Ausprägung
der Asymmetrie der Amplitude bezüglich der x- Achse, weil z. B. eine größere
Verstimmung dabei eine kleinere Amplitude und somit auch eine geringere
Deformierung bewirkt. Oberhalb des instabilen Fixpunkts wird die Amplitude
instabil und divergiert. Zudem befindet man sich oberhalb des
Bifurkationspunktes im chaotischen Regime und der Phasenraum wird aufgespalten.
Die Phasentrajektorien werden abhängig der Verstimmung in unterschiedlicher
Ausprägung zweifach degeneriert, wobei dies eine Periodenverdoppelung, bewirkt.
In der Fourierdomäne wurden anhand der
Rayleigh- Schrödinger Störungsrechnung exakt resonante und parametrisch
resonante Elektronen im nichtlinearen Regime untersucht, welche für die
Generation hoher Harmonischer und Subharmonischer verantwortlich ist. Wie man
sehen konnte, kommen die Resonanzen des gebrochenen Typs erst in den höheren
Näherungen vor und stehen mit dem äußeren Feld nicht mehr in Resonanz. Es wurde
gezeigt, dass bei der Untersuchung der genauen Lösung der Mathieusche´n Differentialgleichung
die möglichen Frequenzen immer dichter werden und letztendlich ein unendliches
Resonanzspektrum entsteht. Der Elektronenresponse wurde an der Resonanz und
deren Umgebung analysiert. Die Untersuchung des asymptotischen
Elektronenresponses zeigte in der nicht approximierten Lösung einen neuen
exotischen Effekt. Für nichtzentrosymmetrische Medien stellte sich eine
frequenzabhängige Amplitude ein, welche nach links kippt. Dieser negative
Skewness Effekt wurde mittels einer Skelettkurve gezeigt, welche an der
Singularität existiert. Die Analyse der Stabilitätsbereiche des
Elektronenresponse in nichtzentrosymmetrischer Materie ergab für externe
Frequenzen oberhalb der nichtlinearen Frequenzantwort eine frequenzabhängige
Amplitudenzunahme und einen starken Amplitudeneinbruch unterhalb des Response
Maximums. Die Amplitude bzw. Intensität wurde
als frequenzabhängige Entwicklung der Fixpunkte des Elektronen- Response
analysiert. Dabei wurden die Amplitudenbereiche unterhalb des
Bifurkationspunktes, genau am Bifurkationspunkt und oberhalb des
Bifurkationspunktes untersucht. Unterhalb des Bifurkationspunktes, liegt
nur eine einzelne reelle stabile Wurzel und eine instabile Wurzel vor. Am
Bifurkationspunkt sowie links des Abrißpunktes existieren alle drei reellen
Amplitudenwerte, wobei die Wurzel  zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte. Für
jeden Wert des optischen Feldes oberhalb seines Bifurkationspunktes, ändert
sich der Charakter der Resonanzerscheinungen. Der Wert des Bifurkationspunktes
entspricht dabei genau dem Wendepunkt der Resonanzkurve. Das ist derjenige Wert
von E, bei dem beide reelle Wurzeln der in b2 quadratischen
Gleichung zusammenfallen, d. h. an der Stelle E = Ek schrumpft der
ganze Abschnitt CD auf einen Wendepunkt zusammen. Aufgrund des instabilen
Zustands bei b=0 benötigt das nichtzentrosymmetrische System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Am
Bifurkationspunkt wurden zwei stabile Gleichgewichtspunkte identifiziert. Die
Frequenz der kleinen Amplitude in der Umgebung des stabilen Fixpunkts ergibt
sich zu
zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte. Für
jeden Wert des optischen Feldes oberhalb seines Bifurkationspunktes, ändert
sich der Charakter der Resonanzerscheinungen. Der Wert des Bifurkationspunktes
entspricht dabei genau dem Wendepunkt der Resonanzkurve. Das ist derjenige Wert
von E, bei dem beide reelle Wurzeln der in b2 quadratischen
Gleichung zusammenfallen, d. h. an der Stelle E = Ek schrumpft der
ganze Abschnitt CD auf einen Wendepunkt zusammen. Aufgrund des instabilen
Zustands bei b=0 benötigt das nichtzentrosymmetrische System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Am
Bifurkationspunkt wurden zwei stabile Gleichgewichtspunkte identifiziert. Die
Frequenz der kleinen Amplitude in der Umgebung des stabilen Fixpunkts ergibt
sich zu 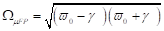 . Für die Nullfrequenz fallen die beiden Wurzeln zusammen und
der Fixpunkt wird instabil. Dies liegt darin begründet, dass geringe
Dämpfungswerte
. Für die Nullfrequenz fallen die beiden Wurzeln zusammen und
der Fixpunkt wird instabil. Dies liegt darin begründet, dass geringe
Dämpfungswerte 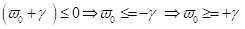 zu instabilen
Schwingungen führen. Dies bewirkt ein Hystereseverhalten. Offensichtlich kippt
die Resonanzkurve bei hohen Anregungsamplituden weg, und man erkennt einen
Sprung in der Resonanzkurve. Dabei zeigte sich, dass die numerischen Werte für
kleine Frequenzen sich entlang dem harmonischen Ast bewegen und für hohe
Frequenzen sich entlang dem anharmonischen Ast entwickeln. Dazwischen zeigt
sich eine Unschärfe im Hystereseverhalten in der Umgebung der
Singularitätsstelle mit verändertem Linienverlauf und veränderter Linienbreite.
Der numerisch erhaltene Response nichtzentrosymmetrischer Materie nimmt von
kleinen Frequenzwerten beginnend gemäß dem harmonischen Ast zu bis in der
Umgebung der Singularitätsstelle die Amplitude auf den anharmonischen Ast
springt und die Kurve über einen geringen Unschärfebereich ausschmiert.
Anschließend nimmt die Amplitude für höhere Frequenzen entlang des
anharmonischen Astes ab. Kommt man von hohen zu niedrigen Frequenzen, nimmt die
Amplitude gemäß dem anharmonischen Astes zu, bis sie schließlich in der
Umgebung der Singularitätsstelle abreißt, auf den harmonischen Ast fällt und
entlang dieser Kurve für abnehmende Frequenzen sich entsprechend verringert.
Die im Fourierraum untersuchte analytische b(
zu instabilen
Schwingungen führen. Dies bewirkt ein Hystereseverhalten. Offensichtlich kippt
die Resonanzkurve bei hohen Anregungsamplituden weg, und man erkennt einen
Sprung in der Resonanzkurve. Dabei zeigte sich, dass die numerischen Werte für
kleine Frequenzen sich entlang dem harmonischen Ast bewegen und für hohe
Frequenzen sich entlang dem anharmonischen Ast entwickeln. Dazwischen zeigt
sich eine Unschärfe im Hystereseverhalten in der Umgebung der
Singularitätsstelle mit verändertem Linienverlauf und veränderter Linienbreite.
Der numerisch erhaltene Response nichtzentrosymmetrischer Materie nimmt von
kleinen Frequenzwerten beginnend gemäß dem harmonischen Ast zu bis in der
Umgebung der Singularitätsstelle die Amplitude auf den anharmonischen Ast
springt und die Kurve über einen geringen Unschärfebereich ausschmiert.
Anschließend nimmt die Amplitude für höhere Frequenzen entlang des
anharmonischen Astes ab. Kommt man von hohen zu niedrigen Frequenzen, nimmt die
Amplitude gemäß dem anharmonischen Astes zu, bis sie schließlich in der
Umgebung der Singularitätsstelle abreißt, auf den harmonischen Ast fällt und
entlang dieser Kurve für abnehmende Frequenzen sich entsprechend verringert.
Die im Fourierraum untersuchte analytische b(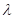 )- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysterescharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" bis zum
Bifurkationswert an, bei dem eine vertikale Tangente erreicht wird. Bei
weiterer Erhöhung der Erregerfrequenzen ändert sich die Amplitude sprunghaft,
d. h. es existiert nur noch eine Lösung auf dem „oberen Ast“ mit negativer Tangente.
Das System muss unstetig auf diesen übergehen. Bei weiterer Erhöhung der
Frequenz verringert sich die Amplitude stetig entlang des "oberen
Astes". Verringert man jetzt wieder die Frequenz so wächst die Amplitude
entlang des oberen Astes bis man zum Peakmaximum kommt. Unterhalb des
Bifurkationspunktes, reißt die Amplitude dann ab und sie fällt sprunghaft auf
den Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren
Astes der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte mit senkrechter Tangente abgegrenzt. Somit kann zusammenfassend
unter Zugrundelegung der numerischen und analytischen Lösung eindeutig eine
negative Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative
Skewness und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen,
welche nicht nur markant von den in der Literatur erforschten Erkenntnissen für
Oberflächen abweicht, sondern auch vom Verhalten des Bulks (mit
Ladungsunterschuss) sowie des Oberflächen / Bulks Übergangs entsprechend ihrer
positiven Skewness markant abweicht. Zudem wurde
das Modell soweit verfeinert, dass mit der hier erhaltenen Lösung und
den entwickelten Programmen auch exakt die Skewness der Amplitude bzw.
Intensität vorhergesagt und beschrieben werden kann. Dies stellt eine enorme
Verbesserung der bisherigen Modellbildung dar, in der die Nichtlinearität als
Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der
Intensität Einfluß nimmt. Die Analyse des nichtlinearen optischen Oberflächen-
Response unter Variation der Dämpfung und der Nichtlinearität ergab folgende
Erkenntnisse: Im Fall vollständig fehlender Nichtlinearität zeigt die Response
Funktion im Fourierraum gewöhnliche Resonanz bei
)- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysterescharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" bis zum
Bifurkationswert an, bei dem eine vertikale Tangente erreicht wird. Bei
weiterer Erhöhung der Erregerfrequenzen ändert sich die Amplitude sprunghaft,
d. h. es existiert nur noch eine Lösung auf dem „oberen Ast“ mit negativer Tangente.
Das System muss unstetig auf diesen übergehen. Bei weiterer Erhöhung der
Frequenz verringert sich die Amplitude stetig entlang des "oberen
Astes". Verringert man jetzt wieder die Frequenz so wächst die Amplitude
entlang des oberen Astes bis man zum Peakmaximum kommt. Unterhalb des
Bifurkationspunktes, reißt die Amplitude dann ab und sie fällt sprunghaft auf
den Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren
Astes der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte mit senkrechter Tangente abgegrenzt. Somit kann zusammenfassend
unter Zugrundelegung der numerischen und analytischen Lösung eindeutig eine
negative Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative
Skewness und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen,
welche nicht nur markant von den in der Literatur erforschten Erkenntnissen für
Oberflächen abweicht, sondern auch vom Verhalten des Bulks (mit
Ladungsunterschuss) sowie des Oberflächen / Bulks Übergangs entsprechend ihrer
positiven Skewness markant abweicht. Zudem wurde
das Modell soweit verfeinert, dass mit der hier erhaltenen Lösung und
den entwickelten Programmen auch exakt die Skewness der Amplitude bzw.
Intensität vorhergesagt und beschrieben werden kann. Dies stellt eine enorme
Verbesserung der bisherigen Modellbildung dar, in der die Nichtlinearität als
Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der
Intensität Einfluß nimmt. Die Analyse des nichtlinearen optischen Oberflächen-
Response unter Variation der Dämpfung und der Nichtlinearität ergab folgende
Erkenntnisse: Im Fall vollständig fehlender Nichtlinearität zeigt die Response
Funktion im Fourierraum gewöhnliche Resonanz bei  , wie sie charakteristisch für Lorentz- Materialien sind. Für
nichtzentrosymmetrische Materie mit
, wie sie charakteristisch für Lorentz- Materialien sind. Für
nichtzentrosymmetrische Materie mit 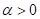 erhält man mit
zunehmender (Feld-)Amplitude eine harte Potentialcharakteristik und die Kurve
zeigt negative Skewness. Negative Nichtlinearität
erhält man mit
zunehmender (Feld-)Amplitude eine harte Potentialcharakteristik und die Kurve
zeigt negative Skewness. Negative Nichtlinearität 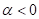 entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Bemerkenswert ist in
diesem Zusammenhang, dass oberhalb des Bifurkationspunktes, eine Erhöhung der
Verstimmung, eine Änderung der Skewness bewirkt, wie sie bislang nur durch
Vorzeichenwechsel der Nichtlinearität zu beobachten war. Die Untersuchung der
Skewness hoher Harmonischer zeigte, eine Skewness welche sich in Abhängigkeit
von der Ordnung der Harmonischen ändert. Für hohe Harmonische konvergiert die
Variation der Skewness. Eine Neue subkritische Bifurkation wurde identifiziert
und eine erweiterte genaue mathematische Lösungsstruktur wurde angegeben.
entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Bemerkenswert ist in
diesem Zusammenhang, dass oberhalb des Bifurkationspunktes, eine Erhöhung der
Verstimmung, eine Änderung der Skewness bewirkt, wie sie bislang nur durch
Vorzeichenwechsel der Nichtlinearität zu beobachten war. Die Untersuchung der
Skewness hoher Harmonischer zeigte, eine Skewness welche sich in Abhängigkeit
von der Ordnung der Harmonischen ändert. Für hohe Harmonische konvergiert die
Variation der Skewness. Eine Neue subkritische Bifurkation wurde identifiziert
und eine erweiterte genaue mathematische Lösungsstruktur wurde angegeben.
2. Zeitliche Entwicklung
der Elektronen- Trajektorie im Phasenraum: Zunächst wird die Kinetik des
Oberflächenelektrons in der Zeitdomäne untersucht werden. Dazu ist es
zweckmäßig, die Grenzflächengleichung 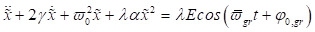 in ein System
gekoppelter Differentialgleichungen 1. Ordnung umzuschreiben.
in ein System
gekoppelter Differentialgleichungen 1. Ordnung umzuschreiben.
|
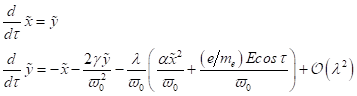
|
(1)
|
mit einer
Genauigkeit von 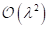 und den Definitionen
und den Definitionen 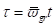 und
und 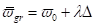 mit
mit 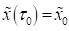 , wobei
, wobei  der Phasenraum ist.
Damit konstruieren wir verschiedene Bilder ebener Phasentrajektorien für
ausgewählte Energiewerte. Es werden folgende Fälle betrachtet:
der Phasenraum ist.
Damit konstruieren wir verschiedene Bilder ebener Phasentrajektorien für
ausgewählte Energiewerte. Es werden folgende Fälle betrachtet:
1. Unterhalb des Bifurkationspunktes: 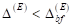
Zuerst betrachten wir kleine optische Felder.
Die Forderung kleiner Felder schließt
chaotisches Verhalten im Phasenraum aus und gewährleistet eine Untersuchung im
nicht chaotischen Regime. Die Fixpunkte, zentraler Fixpunkt 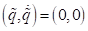 und äußerster Fixpunkt
und äußerster Fixpunkt
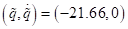 werden untersucht.
Dieser äußerste Fixpunkt wird in der Phasentrajektorie nicht mehr erreicht,
weil er ein instabiler Fixpunkt ist und dieser sich in der Umgebung der
Singularität befindet. Dies ist nicht mehr simulierbar und wird erreicht für
werden untersucht.
Dieser äußerste Fixpunkt wird in der Phasentrajektorie nicht mehr erreicht,
weil er ein instabiler Fixpunkt ist und dieser sich in der Umgebung der
Singularität befindet. Dies ist nicht mehr simulierbar und wird erreicht für 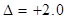 . Die optische Feldstärke nimmt ihren Maximalwert Emax
am Fixpunkt
. Die optische Feldstärke nimmt ihren Maximalwert Emax
am Fixpunkt 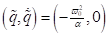 an. Am Ursprung
(zentraler Fixpunkt) des Phasendiagramms verschwindet das optische Feld.
Abbildung (1) zeigt einen Satz von Trajektorien in der (
an. Am Ursprung
(zentraler Fixpunkt) des Phasendiagramms verschwindet das optische Feld.
Abbildung (1) zeigt einen Satz von Trajektorien in der (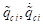 )- Phasenebene für einige ausgewählte Energiewerte bei
konstanter Verstimmung
)- Phasenebene für einige ausgewählte Energiewerte bei
konstanter Verstimmung 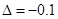 weit unterhalb vom
Bifurkationswert
weit unterhalb vom
Bifurkationswert 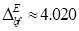 und deren sukzessive
Approximation in die Nähe des Bifurkationswerts. Abbildung (2) zeigt denselben
Satz von Energie Phasenkurven, diesmal aber für den konstanten Verstimmungwert
und deren sukzessive
Approximation in die Nähe des Bifurkationswerts. Abbildung (2) zeigt denselben
Satz von Energie Phasenkurven, diesmal aber für den konstanten Verstimmungwert 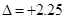 .
.
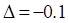 :
:
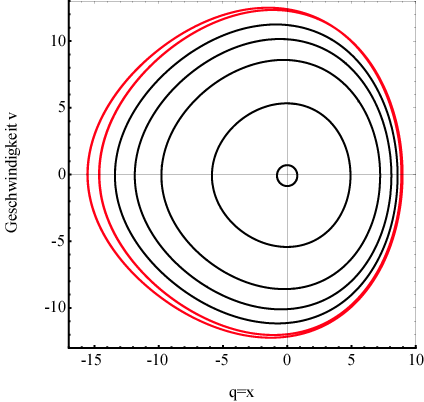
Abbildung 1 zeigt die Energiekonturen im ( )- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=
-0.10, α= 0.046165, E= 0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E = 4.020
(rote Kurve, zeigt den Beginn der Periodenverdoppelung). Die Fixpunkte liegen
bei
)- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=
-0.10, α= 0.046165, E= 0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E = 4.020
(rote Kurve, zeigt den Beginn der Periodenverdoppelung). Die Fixpunkte liegen
bei 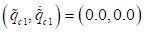 und
und 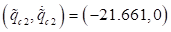 .
.
 :
:
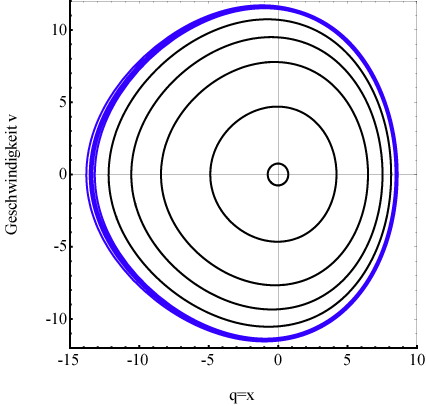
Abbildung 2 zeigt die gleichen Energiekonturen im (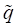 ,
, 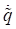 )- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=+2.25,
α= 0.046165, E=0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E=3.6826 (blaue
Kurve, Anfang Periodenverdoppelung). Die Fixpunkte liegen bei
)- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=+2.25,
α= 0.046165, E=0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E=3.6826 (blaue
Kurve, Anfang Periodenverdoppelung). Die Fixpunkte liegen bei 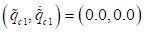 und
und 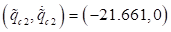 . Hierbei wurde über 8 Perioden integriert
(dicke blaue Kurve) um deren zeitliche Stabilität zu zeigen.
. Hierbei wurde über 8 Perioden integriert
(dicke blaue Kurve) um deren zeitliche Stabilität zu zeigen.
Aus den
Abbildungen (1) und (2) sind für die Trajektorien im Phasenraum kleiner Felder
Kreisbahnen erkennbar. Für höhere optische Felder weicht die Trajektorie
deutlich von Spiral- und Kreisbahnen ab. Es ist eine Asymmetrie der Amplitude
bezüglich der x- Achse zu erkennen, die vom nichtzentrosymmetrischen Potential
herrührt, in dem sich das Elektron bewegt. Oberhalb des instabilen Fixpunkts
bei -200 pm wird die Amplitude instabil und besitzt keinen Limes mehr. Der Satz
von Kurven zeigt zudem, dass bei relativ kleinen Energien, die
Amplitudenbewegungen auf die Umgebung des stabilen Fixpunkts (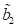 ,0) begrenzt ist und einen homoklinischen loop bildet. In den
höheren Energie- Bereichen, d. h. höherer Beschleunigung des Treiberfeldes,
gibt es einen weiteren Satz von Kurven mit zunehmenden Amplituden, die bis
außerhalb des homoklinischen Loops reichen und die Zunahme des relativen
Anteils der höheren Harmonischen impliziert.
,0) begrenzt ist und einen homoklinischen loop bildet. In den
höheren Energie- Bereichen, d. h. höherer Beschleunigung des Treiberfeldes,
gibt es einen weiteren Satz von Kurven mit zunehmenden Amplituden, die bis
außerhalb des homoklinischen Loops reichen und die Zunahme des relativen
Anteils der höheren Harmonischen impliziert.
2. Oberhalb des Bifurkationspunktes 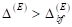
In diesem
Fall können die beiden stabilen Fixpunkte mit den Amplituden 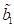 ,
,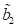 und der instabile
Fixpunkt mit einer Amplitude
und der instabile
Fixpunkt mit einer Amplitude  geordnet werden in der
Reihe,
geordnet werden in der
Reihe,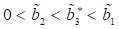 . Die dazu korrespondierenden optischen Energien folgen der
Reihe
. Die dazu korrespondierenden optischen Energien folgen der
Reihe 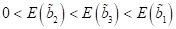 . Bemerkenswert ist, dass die optische Energie ein globales
Maximum beim stabilen Fixpunkt
. Bemerkenswert ist, dass die optische Energie ein globales
Maximum beim stabilen Fixpunkt 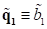 hat und nicht
linksseitig begrenzt ist, wobei die linkseitige Ausprägung von der negativen
Skewness herrührt. Der harmonische Fall ist dagegen links- und rechtsseitig
begrenzt. Im Limes
hat und nicht
linksseitig begrenzt ist, wobei die linkseitige Ausprägung von der negativen
Skewness herrührt. Der harmonische Fall ist dagegen links- und rechtsseitig
begrenzt. Im Limes 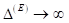 geht die optische
Energie über von
geht die optische
Energie über von 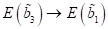 und die Amplituden der
entsprechenden Fixpunkte nähern sich einander an. Für Energiewerte im Bereich
und die Amplituden der
entsprechenden Fixpunkte nähern sich einander an. Für Energiewerte im Bereich 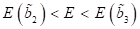 bzw.
bzw. 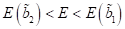 , gibt es eine zweifache Degeneration der Kurve(n). Dies
tritt ein weil wenn wir vom instabilen Fixpunkt mit Amplitude
, gibt es eine zweifache Degeneration der Kurve(n). Dies
tritt ein weil wenn wir vom instabilen Fixpunkt mit Amplitude  weggehen und nach
positiven x- Werten fortsetzen, die Energie zunächst abnimmt ohne am Wert
weggehen und nach
positiven x- Werten fortsetzen, die Energie zunächst abnimmt ohne am Wert 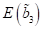 gebunden zu sein und
durch diesen begrenzt zu werden. Währenddessen, wenn wir nach negativen x-
Werten fortfahren, nimmt ab dem Degenerationspunkt die Energie bis zum Maximum
bei
gebunden zu sein und
durch diesen begrenzt zu werden. Währenddessen, wenn wir nach negativen x-
Werten fortfahren, nimmt ab dem Degenerationspunkt die Energie bis zum Maximum
bei 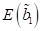 beim stabilen Fixpunkt
beim stabilen Fixpunkt
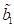 schnell zu, um bei
noch negativeren x- Werten die Energie schnell wieder auf ein Minimum bei
schnell zu, um bei
noch negativeren x- Werten die Energie schnell wieder auf ein Minimum bei 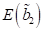 beim stabilen Fixpunkt
beim stabilen Fixpunkt
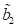 abzugeben. Die
Abbildungen (3) und (4) zeigen die optischen Feldkonturen oberhalb des
Bifurkationspunktes
abzugeben. Die
Abbildungen (3) und (4) zeigen die optischen Feldkonturen oberhalb des
Bifurkationspunktes 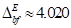 für die
Verstimmungswerte ∆= +2.25 und ∆= -0.1. Für hohe Verstimmungswerte,
wie sie für maximale Spinströme und deren Umgebung auftreten, gibt es zwei
relativ kleine Amplitudenbewegungen um den stabilen Fixpunkt (
für die
Verstimmungswerte ∆= +2.25 und ∆= -0.1. Für hohe Verstimmungswerte,
wie sie für maximale Spinströme und deren Umgebung auftreten, gibt es zwei
relativ kleine Amplitudenbewegungen um den stabilen Fixpunkt (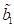 ,0) herum und eine weitere große Amplitude die außerhalb des
homoklinischen Loops liegt bei (
,0) herum und eine weitere große Amplitude die außerhalb des
homoklinischen Loops liegt bei (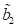 ,0). Insgesamt liegt eine Periodenverdoppelung vor,
,0). Insgesamt liegt eine Periodenverdoppelung vor, 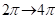 . Für niedrigere Verstimmungswerte gibt es zwei
Amplitudenbewegungen mit etwas unterschiedlichen Amplitudenausprägungen um den
stabilen Fixpunkt (
. Für niedrigere Verstimmungswerte gibt es zwei
Amplitudenbewegungen mit etwas unterschiedlichen Amplitudenausprägungen um den
stabilen Fixpunkt (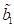 ,0) herum und bilden einen homoklinischen Loop der bis zum
Fixpunkt (
,0) herum und bilden einen homoklinischen Loop der bis zum
Fixpunkt (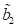 ,0) reicht. Insgesamt liegt ebenfalls eine
Periodenverdoppelung vor,
,0) reicht. Insgesamt liegt ebenfalls eine
Periodenverdoppelung vor, 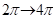 , welche aber in
diesem Fall niedrigerer Verstimmungswerte sich stärker ausgeprägt zeigt. Dies
beschreibt das Verhalten maximaler Ladungsströme und deren hinreichend kleiner
Umgebung um diese, welche eine ausgeprägte Degeneration der Amplitude und
Frequenzabhängigkeit verursacht. Letztendlich ergeben sich damit für Photo- und
Spinströme jeweils eine Aufspaltung des Phasenraums oberhalb des
Bifurkationspunktes, aber in unterschiedlicher Ausprägung. Dies führt zu einer
Degeneration und Skewness der Anregungsamplitude. Aus diesem Grund ist
gegenüber den Spinströmen eine leichtere und stärkere Photostromgeneration mit
höherer Reichweite zu erwarten.
, welche aber in
diesem Fall niedrigerer Verstimmungswerte sich stärker ausgeprägt zeigt. Dies
beschreibt das Verhalten maximaler Ladungsströme und deren hinreichend kleiner
Umgebung um diese, welche eine ausgeprägte Degeneration der Amplitude und
Frequenzabhängigkeit verursacht. Letztendlich ergeben sich damit für Photo- und
Spinströme jeweils eine Aufspaltung des Phasenraums oberhalb des
Bifurkationspunktes, aber in unterschiedlicher Ausprägung. Dies führt zu einer
Degeneration und Skewness der Anregungsamplitude. Aus diesem Grund ist
gegenüber den Spinströmen eine leichtere und stärkere Photostromgeneration mit
höherer Reichweite zu erwarten.
∆=
+2.25:
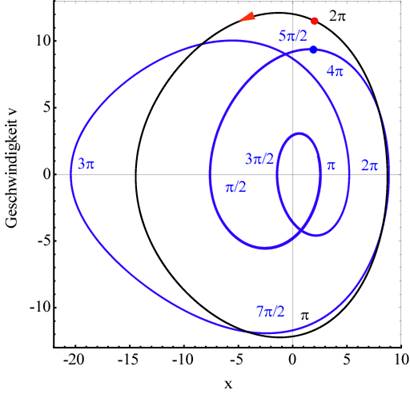
Abbildung 3 zeigt
die Periodenverdoppelungs- Kaskade: Konstante Energiekonturen im (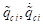 )- Phasenraum (Energievariation) oberhalb des
Bifurkationspunkts für eine Verstimmung ∆=+2.25; α= 0.046165,
E=3.7108 (blaue Kurve, Periodenverdoppelung) und für E= 4.3157 (rote Kurve,
eine Periode). Die Fixpunkte liegen bei
)- Phasenraum (Energievariation) oberhalb des
Bifurkationspunkts für eine Verstimmung ∆=+2.25; α= 0.046165,
E=3.7108 (blaue Kurve, Periodenverdoppelung) und für E= 4.3157 (rote Kurve,
eine Periode). Die Fixpunkte liegen bei 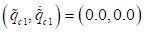 und
und 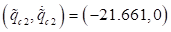 .
.
∆=-0.1:
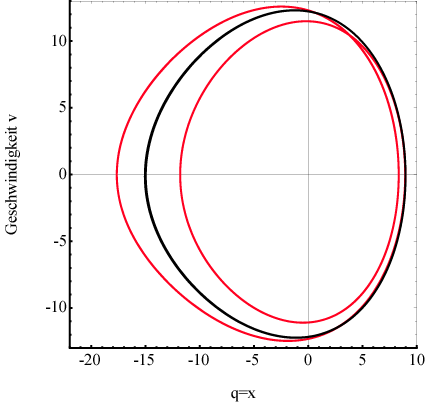
Abbildung 4 zeigt
die gleichen Energiekonturen im (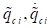 )- Phasenraum für eine Verstimmung (Energievariation)
oberhalb des Bifurkationspunkts / -werts; α= 0.046165, ∆=-0.1,
E=4.18033 (rote Kurve, Periodenverdoppelung) und für E= 4.0 (schwarze Kurve,
eine Periode). Die Fixpunkte liegen bei
)- Phasenraum für eine Verstimmung (Energievariation)
oberhalb des Bifurkationspunkts / -werts; α= 0.046165, ∆=-0.1,
E=4.18033 (rote Kurve, Periodenverdoppelung) und für E= 4.0 (schwarze Kurve,
eine Periode). Die Fixpunkte liegen bei 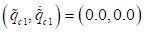 und
und 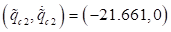 .
.
3. Asymptotische
Elektronenresponse: Aufbau und Stabilität: In diesem Abschnitt betrachten wir
den Elektronenresponse während des Durchgangs durch die Resonanzstelle(n)
nichtzentrosymmetrischer Materie. Dabei soll die Änderung des optischen Feldes
als hinreichend langsam angesehen werden. Wir betrachten nun die möglichen
Resonanzfälle NZS- Materie. Nach Voraussetzung liegen die Ultrasubharmonischen
sowie die hohen Harmonischen hinreichend nahe bei der natürlichen
Resonanzfrequenz, d. h. 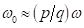 . Damit können wir die kleine Verstimmung
. Damit können wir die kleine Verstimmung 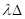 zwischen dem Quadrat
der natürlichen Systemfrequenz und Erregerfrequenz einführen mit:
zwischen dem Quadrat
der natürlichen Systemfrequenz und Erregerfrequenz einführen mit:
|
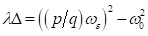
|
(2)
|
und dem
optischen Feld zuordnen:
|
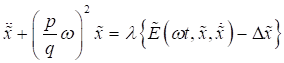
|
(3)
|
mit 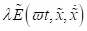 als ein Polynom
bezüglich der Polarisation
als ein Polynom
bezüglich der Polarisation 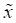 und
und 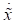 , das noch eine endliche Zahl von hohen Harmonischen und
Subharmonischen nach der Variablen
, das noch eine endliche Zahl von hohen Harmonischen und
Subharmonischen nach der Variablen 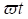 enthält. Hierbei ist
zu beachten, dass für nichtzentrosymmetrische Materie die Resonanzmenge
enthält. Hierbei ist
zu beachten, dass für nichtzentrosymmetrische Materie die Resonanzmenge 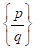 nicht beliebig dicht
sein kann, sondern sich vielmehr nur Wertepaaren, p und q ϵ
nicht beliebig dicht
sein kann, sondern sich vielmehr nur Wertepaaren, p und q ϵ 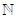 , für geradzahlige Resonanzen nähern und auf diese Menge
beschränkt sind. Mithilfe der aus der Störungsrechnung gewonnenen Erkenntnisse
können wir die Amplituden- und Frequenzentwicklung des Ein- Teilchen- Systems
in NZS- Materie formulieren. Dabei ist während des Resonanzdurchgangs nur der
Phasenunterschied
, für geradzahlige Resonanzen nähern und auf diese Menge
beschränkt sind. Mithilfe der aus der Störungsrechnung gewonnenen Erkenntnisse
können wir die Amplituden- und Frequenzentwicklung des Ein- Teilchen- Systems
in NZS- Materie formulieren. Dabei ist während des Resonanzdurchgangs nur der
Phasenunterschied 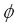 mit Verstimmung
zwischen dem externen optischen Feld und der Eigenschwingung des Systems
relevant.
mit Verstimmung
zwischen dem externen optischen Feld und der Eigenschwingung des Systems
relevant.
|
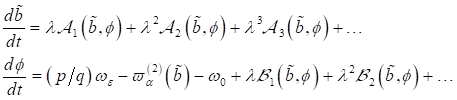
|
(4)
|
wobei die
Funktionen 
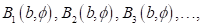 und
und 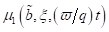 ,
, 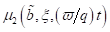 partikuläre, 2 π
periodische Lösungen des Systems sind. Für Phasenunterschiede
partikuläre, 2 π
periodische Lösungen des Systems sind. Für Phasenunterschiede 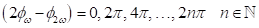 lassen sich maximale
Photoströme und
lassen sich maximale
Photoströme und 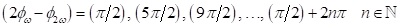 Spinströme bzw. mit
Spinströme bzw. mit 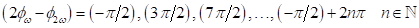 umgepolte Spinströme
anregen. Diese Funktionen lassen sich derart bestimmen dass sie die
Hauptgleichung erfüllt. Dazu
differenzieren wir die Formulierung einer endlichen Anzahl von Harmonischen und
Subharmonischen mit
umgepolte Spinströme
anregen. Diese Funktionen lassen sich derart bestimmen dass sie die
Hauptgleichung erfüllt. Dazu
differenzieren wir die Formulierung einer endlichen Anzahl von Harmonischen und
Subharmonischen mit 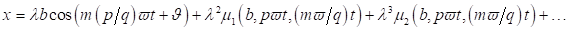 unter Berücksichtigung
der beiden zeitabhängigen Funktionen
unter Berücksichtigung
der beiden zeitabhängigen Funktionen 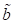 und
und 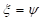 .
.
|
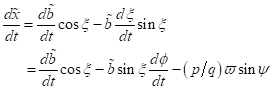
|
(5)
|
Es existiert
unter Berücksichtigung der beiden zeitabhängigen Funktionen mit
|
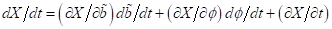
|
(6)
|
ein
vollständiges Differential.
|
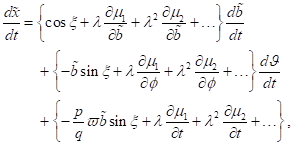
|
(7)
|
Insgesamt
lassen sich damit die Differentiale in Abhängigkeit des Parameters λ
bestimmen zu:
|
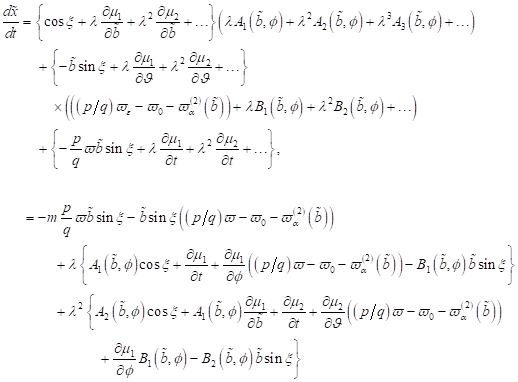
|
(8)
|
Formal
erhält man analog:
|
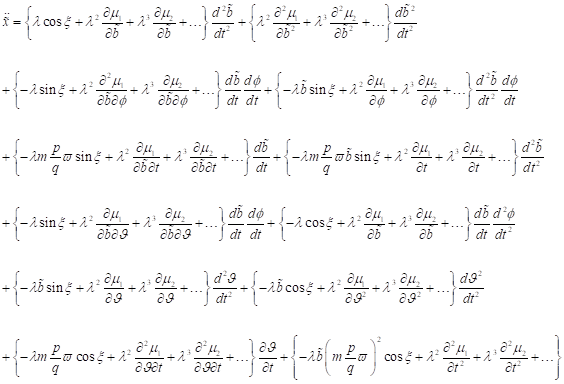
|
(9)
|
bzw. in
kompakterer Darstellung:
|
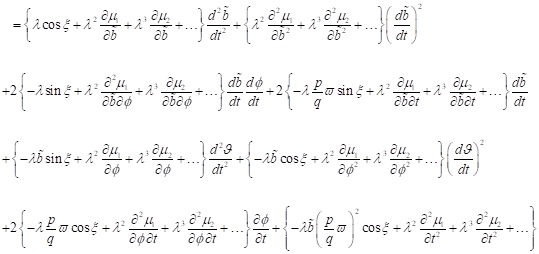
|
(10)
|
Zudem
ergeben sich die differentiellen Beziehungen:
|
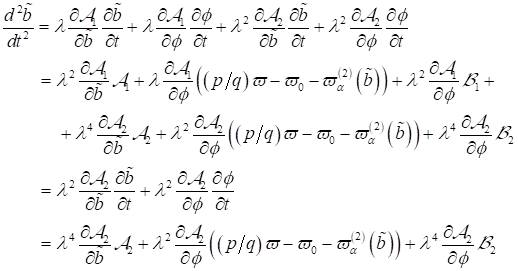
|
(11)
|
|
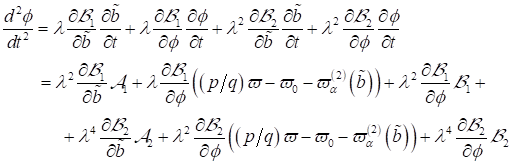
|
(12)
|
|
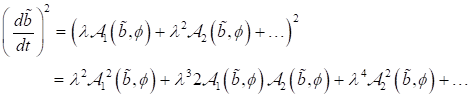
|
(13)
|
|
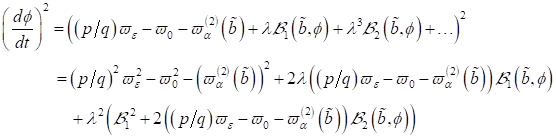
|
(14)
|
|
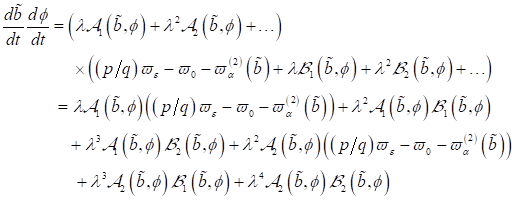
|
(15)
|
Unter
anderem durch Berücksichtigung von (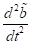 ,
, 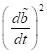 ,
, 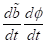 ,
, 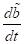 ,
, 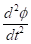 ,
, 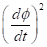 ,
, 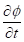 ) erhalten wir über die beiden analytischen Ausdrücke die zu
lösende Differentialgleichung für die Dynamik des Elektrons in disspiativer
Umgebung gemäß:
) erhalten wir über die beiden analytischen Ausdrücke die zu
lösende Differentialgleichung für die Dynamik des Elektrons in disspiativer
Umgebung gemäß:
|
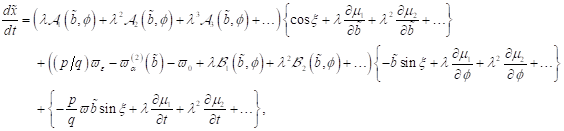
|
(16)
|
|
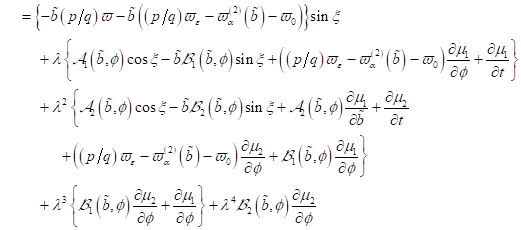
|
(17)
|
und
|
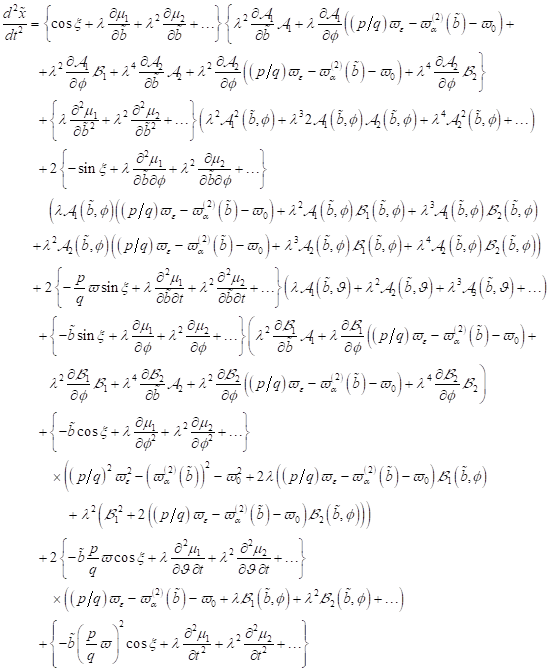
|
(18)
|
In Potenzen
des kleinen Parameters λ können wir bis zu kleinen Größen vierter Ordnung
anschreiben:
|
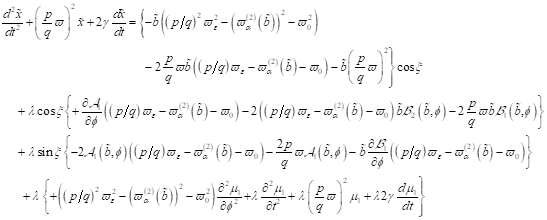
|
(19)
|
|
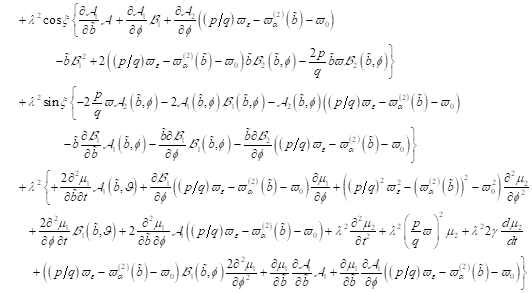
|
(20)
|
|
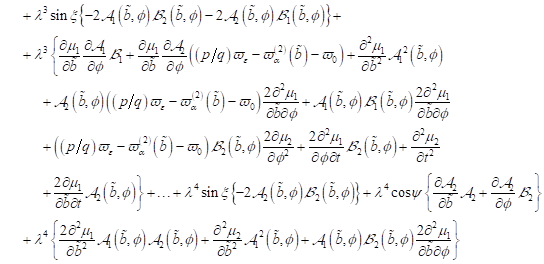
|
(21)
|
Wir entwickeln die Erregerkraft
nach Potenzen des kleinen Parameters λ und
finden:
|
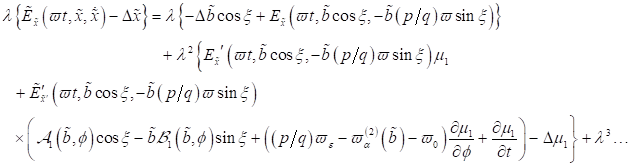
|
(22)
|
Mittels Koeffizientenvergleich
erhalten wir folgendes Gleichungssystem für kleine Größen in λ und λ2
zur Bestimmung der gesuchten Funktionen mit
|
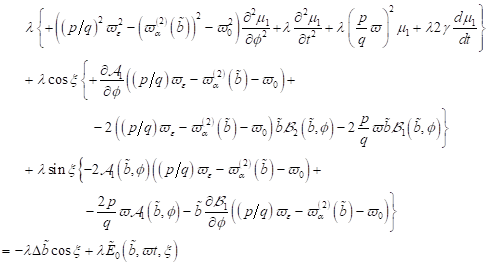
|
(23)
|
und
|
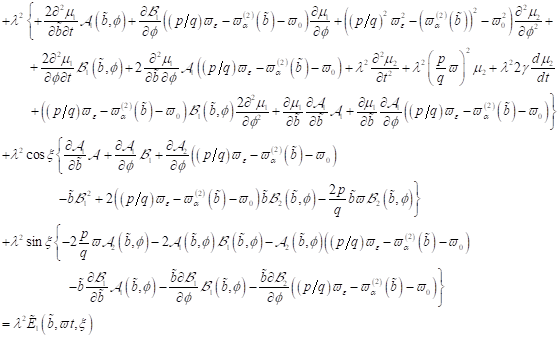
|
(24)
|
Damit können wir die gesuchten
Funktionen bestimmen und erhalten:
|
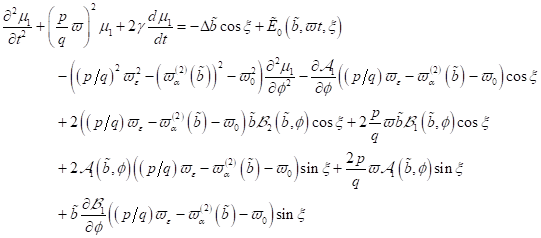
|
(25)
|
und
|
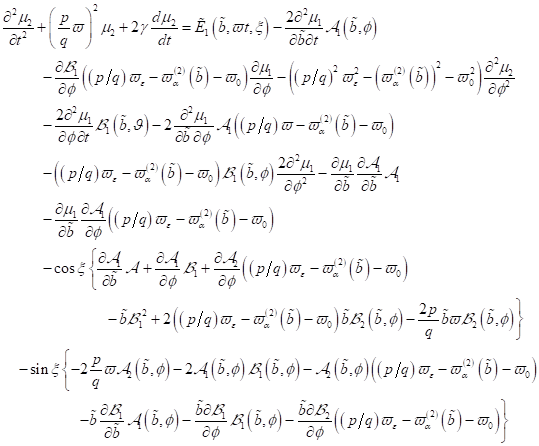
|
(26)
|
mit den
eingeführten Bezeichnungen:
|
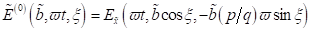
|
(27)
|
und
|
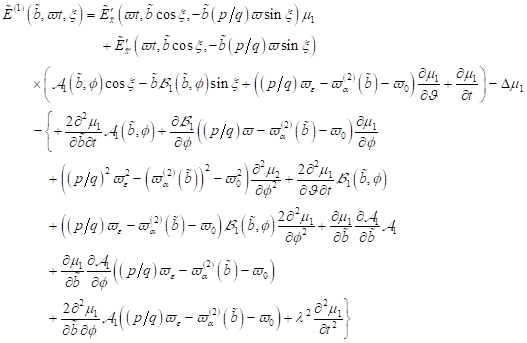
|
(28)
|
Indem wir
die Funktionen 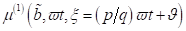 und
und 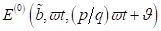 in Form endlicher
Fouriersummen darstellen, können wir allgemein für hohe Harmonische und
(U)SubHG scheiben:
in Form endlicher
Fouriersummen darstellen, können wir allgemein für hohe Harmonische und
(U)SubHG scheiben:
|
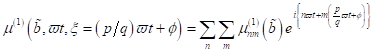
|
(29)
|
und
|
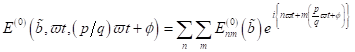
|
(30)
|
wobei das optische
Feld in Fourierkomponenten zerlegt werden kann und jede Komponente einzeln
behandelt wird.
|
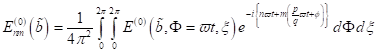
|
(31)
|
Weiters
erhalten wir:
|
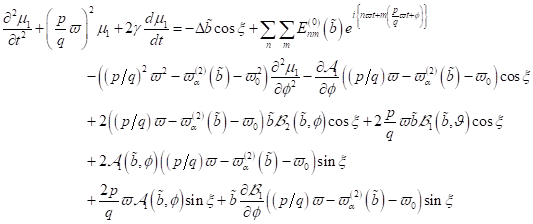
|
(32)
|
einen
analytischen Ausdruck als Ergebnis des allgemein entwickelten Falles für NZS
gebundene Elektronen in der Umgebung von dissipativen Resonanzgebieten, die den
Fall exakt resonanter Elektronen beinhaltet.
|
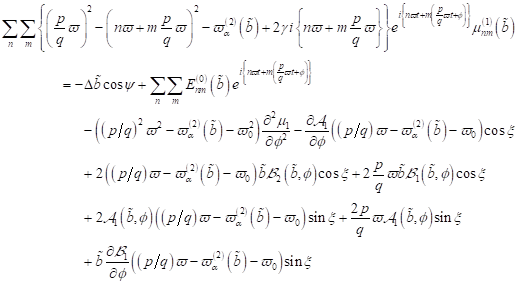
|
(33)
|
mit den
beiden Differentialquotienten:
|
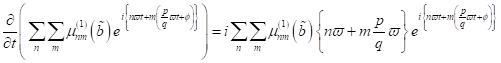
|
(34)
|
und
|
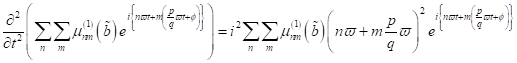
|
(35)
|
Durch
Koeffizientenvergleich erhalten wir den allgemeinen analytischen Ausdruck für
die behobenen elektronischen exakten Singularitäten und deren dissipativer
Umgebung 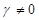 für alle n und m in
Form der Beziehung:
für alle n und m in
Form der Beziehung:
|
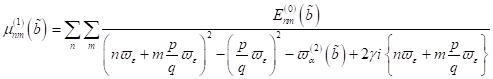
|
(36)
|
wobei diese
Gleichung den Spezialfall der Singularitäten in nichtdissipativer Umgebung (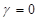 ) beinhaltet, welche für alle n und m der Bedingung genügen:
) beinhaltet, welche für alle n und m der Bedingung genügen:
|
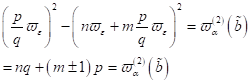
|
(37)
|
d. h. an der
Singularität existiert die Skelettkurve. Damit erhalten wir für die exakt
resonante NZS gebundenen Elektronen mit
|
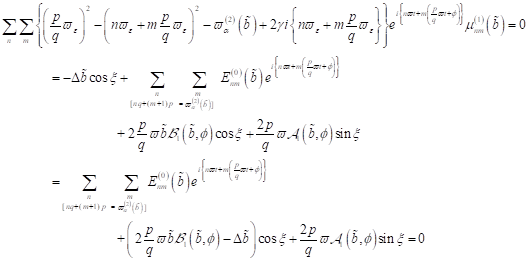
|
(38)
|
in Form
ihrer exakten Resonanzstellen, welche als longitudinale Moden im Festkörper
propagieren:
|
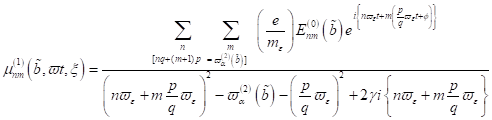
|
(39)
|
Für das
Übergangsgebiet zur Resonanzzone NZS- Materie finden so für die Umgebung der
Resonanzen 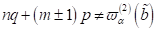 :
:
|
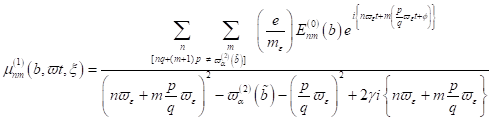
|
(40)
|
Berücksichtigt
man Anregungen von Photo- und Spinströmen durch hohe Harmonische und
Subharmonische beliebiger Kombination der Form 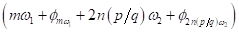 so erhält man:
so erhält man:
|
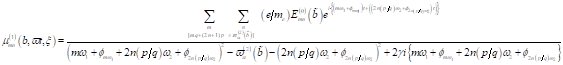
|
(41)
|
Damit ergibt
sich für angeregte Photo und Spinströme folgende neue Lösungsstruktur an der
Singularität und deren hinreichend kleiner Umgebung zu
|
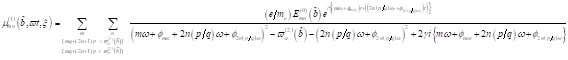
|
(42)
|
Für sehr
hohe Harmonische unter Ausschluss der Grundschwingungsresonanz können wir für
das Resonanzgebiet und deren Umgebung folgende Lösungsstruktur formulieren:
|
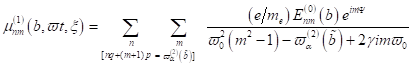
|
(43)
|
|
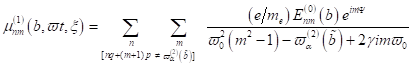
|
(44)
|
|
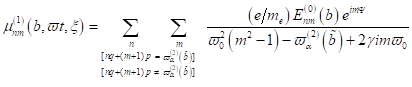
|
(45)
|
Dabei werden
in dieser Summe alle integer n, m einschließlich der Null berücksichtigt.
Folglich existieren in der Summe komplexe Exponenten der Form:
|
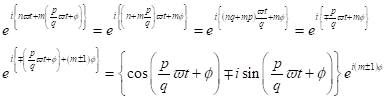
|
(46)
|
Da q ein
Teiler von 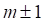 ist, können wir diesen
Faktor für
ist, können wir diesen
Faktor für 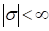 d. h.
d. h. 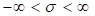 schreiben als
schreiben als 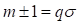
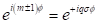 weil
weil 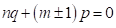 ist.
Koeffizientenvergleich der trigonometrischen Funktionen
ist.
Koeffizientenvergleich der trigonometrischen Funktionen 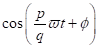 und
und 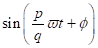 liefert die Änderung
der Amplitude und der rotierenden Phasen in Abhängigkeit der Parameter
liefert die Änderung
der Amplitude und der rotierenden Phasen in Abhängigkeit der Parameter 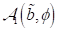 und
und 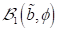 :
:
|
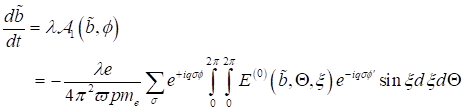
|
(47)
|
und
|
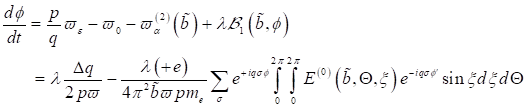
|
(48)
|
Dies
beinhaltet den allgemeinen Fall unter Berücksichtigung der Verstimmung erster
Ordnung 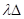 . Für Resonanzfälle ist die Verstimmung im Allgemeinen eine
kleine Größe und kann mit der gleichen Genauigkeit in der Form
. Für Resonanzfälle ist die Verstimmung im Allgemeinen eine
kleine Größe und kann mit der gleichen Genauigkeit in der Form 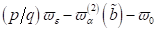 berücksichtigt werden.
In der ersten Näherung schwingt das System mit einer Frequenz, die genau (p/q)
ω entspricht und befindet sich somit in einem einfachen rationalen
Verhältnis zur optischen Erregerfrequenz. In den höheren Näherungen, erhalten
wir ein stationäres Schwingungssystem, welche periodische Lösungen von sind. In
berücksichtigt werden.
In der ersten Näherung schwingt das System mit einer Frequenz, die genau (p/q)
ω entspricht und befindet sich somit in einem einfachen rationalen
Verhältnis zur optischen Erregerfrequenz. In den höheren Näherungen, erhalten
wir ein stationäres Schwingungssystem, welche periodische Lösungen von sind. In
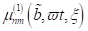 treten neben der
Grundschwingung (p/q) ω0, noch weitere „exotische“ Schwingungen
auf, die Teilwerten der Grundfrequenz entsprechen, (m /q) ω mit m
treten neben der
Grundschwingung (p/q) ω0, noch weitere „exotische“ Schwingungen
auf, die Teilwerten der Grundfrequenz entsprechen, (m /q) ω mit m 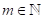 . Die Änderung der Amplitude und die rotierenden Phasen
werden in Abhängigkeit der Parameter
. Die Änderung der Amplitude und die rotierenden Phasen
werden in Abhängigkeit der Parameter 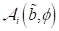 und
und 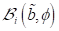 formuliert, wobei wir
als erste und zweite Näherung kleiner Größen für den allgemeinen Fall
formuliert, wobei wir
als erste und zweite Näherung kleiner Größen für den allgemeinen Fall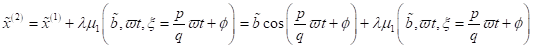 vorausgesetzt haben
wobei p und q kleine ganze teilerfremde Zahlen sind. Dabei lassen sich
vorausgesetzt haben
wobei p und q kleine ganze teilerfremde Zahlen sind. Dabei lassen sich 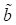 und
und 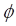 für den speziellen
Fall nichtzentrosymmetrischer Materie mit folgendem entwickeltem
Gleichungssystem analytisch bestimmen.
für den speziellen
Fall nichtzentrosymmetrischer Materie mit folgendem entwickeltem
Gleichungssystem analytisch bestimmen.
|
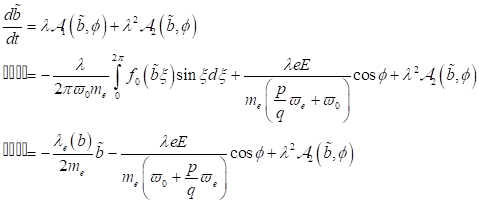
|
(49)
|
|
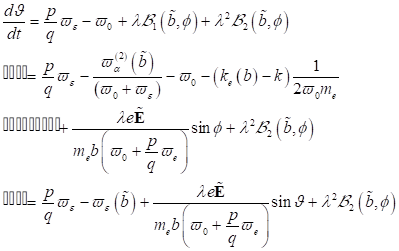
|
(50)
|
wobei direkt
an der Resonanzstelle entwickelt wurde, mit 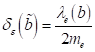 als äquivalentes
Dämpfungsdekrement und
als äquivalentes
Dämpfungsdekrement und 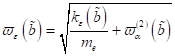 als äquivalente
Frequenz der nichtlinearen Resonanzschwingungen induziert durch Wechselwirkung
von NZS- Materie mit photonischen Feldern. Dabei entsprechen die eingeführten
Parameter
als äquivalente
Frequenz der nichtlinearen Resonanzschwingungen induziert durch Wechselwirkung
von NZS- Materie mit photonischen Feldern. Dabei entsprechen die eingeführten
Parameter 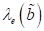 wieder einem
äquivalenten Dämpfungskoeffizienten und
wieder einem
äquivalenten Dämpfungskoeffizienten und 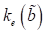 einer äquivalenten
Gesamtfederkonstanten des betrachteten NZS Schwingungssystems, dass sich beim
Fehlen einer äußeren Erregung in einem „freien“ Zustand befindet. Dies ist
somit ein System, dass durch eine dissipative Differentialgleichung der Form
einer äquivalenten
Gesamtfederkonstanten des betrachteten NZS Schwingungssystems, dass sich beim
Fehlen einer äußeren Erregung in einem „freien“ Zustand befindet. Dies ist
somit ein System, dass durch eine dissipative Differentialgleichung der Form 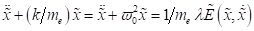 hinreichend
beschrieben werden kann. Wir betrachten die stationären Schwingungszustände mit
hinreichend
beschrieben werden kann. Wir betrachten die stationären Schwingungszustände mit
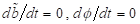 und erhalten die
stationären Werte für die Amplitude
und erhalten die
stationären Werte für die Amplitude 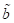 und Phase
und Phase 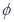 in erster Näherung:
in erster Näherung:
|
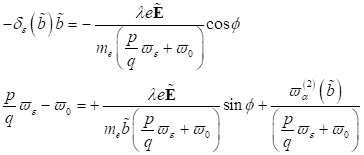
|
(51)
|
Wie man
daraus ersehen kann, ist die Schwingung nicht mehr rein sinusförmig und der
Skew mit 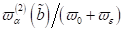 wird wirksam
für exakt resonante Elektronen.
wird wirksam
für exakt resonante Elektronen.
|
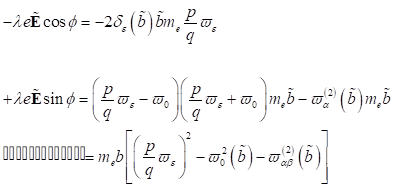
|
(52)
|
Eliminierung
der Phase 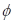 liefert die
analytische Lösung :
liefert die
analytische Lösung :
|
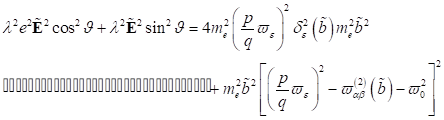
|
(53)
|
Daraus
erhalten wir die Frequenzabhängigkeit des Elektronenresponses vom äußeren
optischen Feld:
|
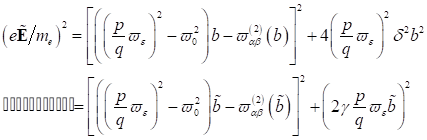
|
(54)
|
Wir
untersuchen nun die Stabilitätsbereiche des Elektronenresponses in
nichtzentrosymmetrischer Materie. Auf der Basis der vorhergehenden
Betrachtungen für nichtzentrosymmetrische Medien mit einer Genauigkeit bis zu
kleinen Größen zweiter Ordnung erhalten wir die Variationsgleichungen in Form:
|
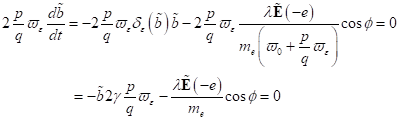
|
(55)
|
|
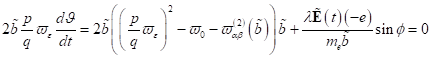
|
(56)
|
wobei mit 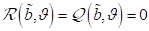 für stationäre,
synchrone Zustände nichtzentrosymmetrisch gebundener Grenzflächenelektronen
gilt:
für stationäre,
synchrone Zustände nichtzentrosymmetrisch gebundener Grenzflächenelektronen
gilt:
|
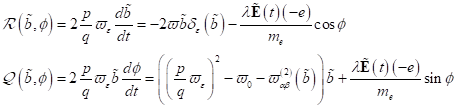
|
(57)
|
Die
charakteristische Gleichung für dieses System besitzt die Form:
|
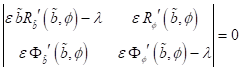
|
(58)
|
das heißt
|
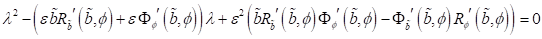
|
(59)
|
Damit
erhalten wir die folgenden Stabilitätsbedingungen der synchronen, stationären
Zustände:
|
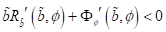
|
(60)
|
|
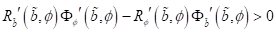
|
(61)
|
Die erste
Bedingung ist für gewöhnliche Dämpfungsgesetze immer erfüllt. Das bedeutet, die
mittlere Leistung W(b) nimmt mit der Amplitude zu und die Änderung der
mittleren Leistung ist positiv W´(b)>0. Die Untersuchung der 2. Bedingung
erfolgt über die vorhergehenden Lösungen. Dazu betrachten wir die
Frequenzabhängigkeit der Amplitude b und der Phase ɸ. Mit Rücksicht auf
die eingeführten Bezeichnungen
|
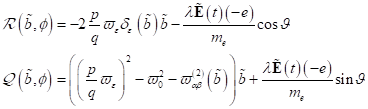
|
(62)
|
können wir
die zeitliche Variation bestimmen zu
|
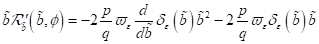
|
(63)
|
|
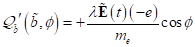
|
(64)
|
Weiters
finden wir:
|
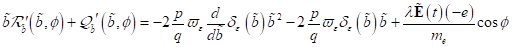
|
(65)
|
Analoge
Betrachtungen der Differentiale in Abhängigkeit der eingestrahlten optischen
Frequenzen liefern:
|
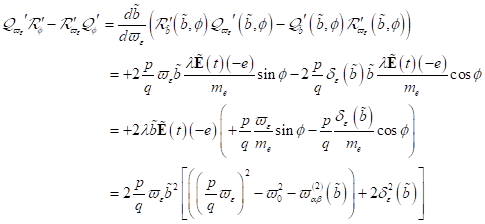
|
(66)
|
wobei
|
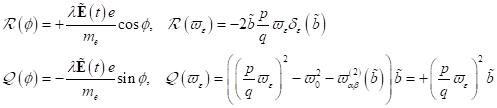
|
(67)
|
und
|
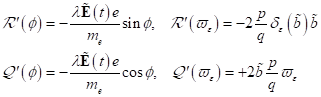
|
(68)
|
mit
|
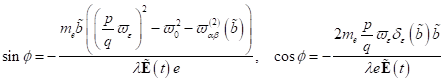
|
(69)
|
Wir erhalten insgesamt:
|
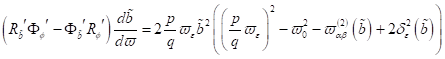
|
(70)
|
Damit können
wir die anfangs angesetzte Stabilitätsbedingung sofort in folgende analytisch
aussagekräftige Form für nichtzentrosymmetrische Materie anschreiben
|
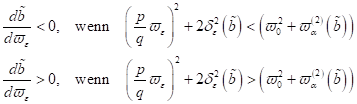
|
(71)
|
bzw. mit
einer Genauigkeit bis zu kleinen Größen erster Ordnung:
|
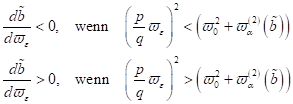
|
(72)
|
und für den
Fall zentrosymmetrischer Materie
|
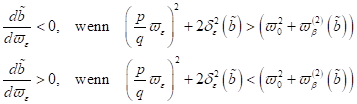
|
(73)
|
mit einer
Genauigkeit bis zu kleinen Größen erster Ordnung:
|
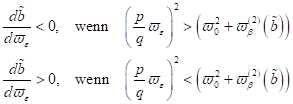
|
(74)
|
D. h.
solange die externen Frequenzen oberhalb (bzw. unterhalb für N.Z.S) der
nichtlinearen Frequenzantwort 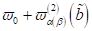 sind, nimmt die
Amplitude in Abhängigkeit der Frequenz zu und bricht stark unterhalb des
instabilen Response Maximalwertes ein.
sind, nimmt die
Amplitude in Abhängigkeit der Frequenz zu und bricht stark unterhalb des
instabilen Response Maximalwertes ein.
3. Fixpunktamplitude: Mit 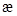 als nichtlinearen
Koeffizienten der Anharmonizität, welche die Frequenzkorrektur beschreibt,
finden wir die Lösungsstruktur für die Amplituden in den jeweiligen Näherungen.
Dabei ist zu berücksichtigen, dass
als nichtlinearen
Koeffizienten der Anharmonizität, welche die Frequenzkorrektur beschreibt,
finden wir die Lösungsstruktur für die Amplituden in den jeweiligen Näherungen.
Dabei ist zu berücksichtigen, dass 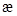 mit einer Genauigkeit
von
mit einer Genauigkeit
von 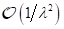 in die Berechnungen
mit eingeht. Für nichtzentrosymmetrische Materie in der Näherung kleiner Größen
bis 2. Ordnung, gültig für Frequenzintervalle
in die Berechnungen
mit eingeht. Für nichtzentrosymmetrische Materie in der Näherung kleiner Größen
bis 2. Ordnung, gültig für Frequenzintervalle 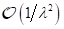 , können wir damit anschreiben:
, können wir damit anschreiben:
|
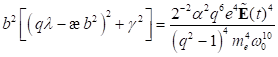
|
(75)
|
|
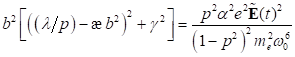
|
(76)
|
mit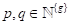 für
nichtzentrosymmetrische Medien bzw. in der parametrischen Schwingung mit der
Lösung der Mathieuschen Differentialgleichung mit einer Genauigkeit von
für
nichtzentrosymmetrische Medien bzw. in der parametrischen Schwingung mit der
Lösung der Mathieuschen Differentialgleichung mit einer Genauigkeit von  . Bemerkenswert ist hierbei, dass für steigende Ordnungen die
SubHG- Amplituden zunehmen. Die HHG Ordnungen werden dagegen mit kleiner
werdender Amplitude generiert.
. Bemerkenswert ist hierbei, dass für steigende Ordnungen die
SubHG- Amplituden zunehmen. Die HHG Ordnungen werden dagegen mit kleiner
werdender Amplitude generiert.
|
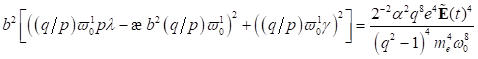
|
(77)
|
|
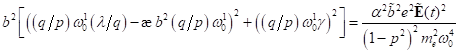
|
(78)
|
Damit finden
wir als mögliche Amplitudenwerte neben der trivialen Wurzel
|
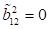
|
(79)
|
folgende
Wurzeln für HHG & (U)SubHG:
|
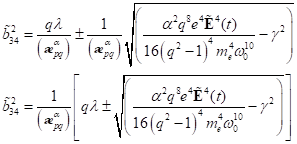
|
(80)
|
|
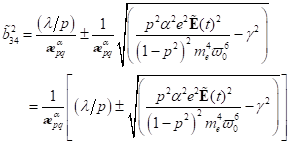
|
(81)
|
mit p, q 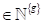 für
nichtzentrosymmetrische Medien. Die erste Gleichung führt zu der einzigen
Möglichkeit b=0, einer doppelten Nullstelle. Für den Fall, dass
für
nichtzentrosymmetrische Medien. Die erste Gleichung führt zu der einzigen
Möglichkeit b=0, einer doppelten Nullstelle. Für den Fall, dass 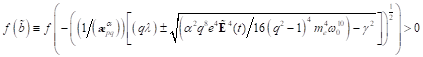 und
und
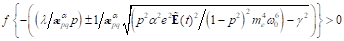 ist, gibt es drei
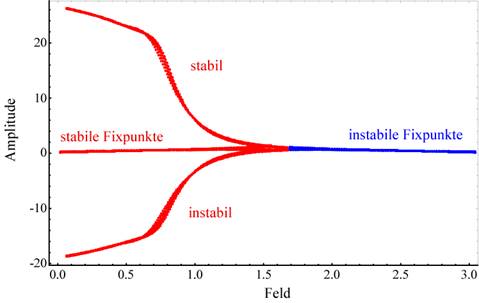
reelle Wurzeln. Dies ist der Fall unterhalb des Bifurkationspunktes, z. B. wenn
ist, gibt es drei
reelle Wurzeln. Dies ist der Fall unterhalb des Bifurkationspunktes, z. B. wenn
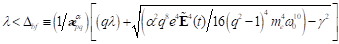 und
und
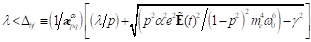 . Unter Berücksichtigung der positiven Werte von den sechs
Möglichkeiten der Fixpunktanordnung erhalten wir die drei zu berücksichtigenden
stabilen Fixpunkte bei:
. Unter Berücksichtigung der positiven Werte von den sechs
Möglichkeiten der Fixpunktanordnung erhalten wir die drei zu berücksichtigenden
stabilen Fixpunkte bei:
|
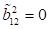
|
(82)
|
|
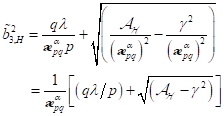
|
(83)
|
|
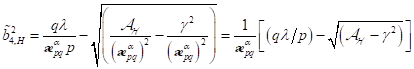
|
(84)
|
|
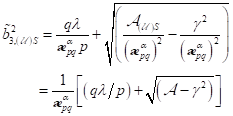
|
(85)
|
|
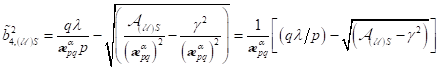
|
(86)
|
Diese
Fixpunkte gehorchen der Reihe:
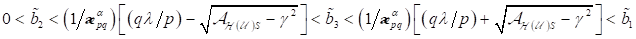
Bemerkenswert
ist hierbei das Ergebnis für nichtzentrosymmetrische Systeme, wo eine neue
subkritische Bifurkation vorliegt. Rechts vom Punkt B, d. h. oberhalb des
Bifurkationspunktes, 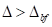 ,
, 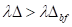 liegt nur eine verschwindende
reelle Wurzel
liegt nur eine verschwindende
reelle Wurzel 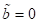 vor, d. h. hier
werden keine Resonanzschwingungen angeregt. Zwischen dem Intervall B und C, d.
h. unterhalb des Bifurkationspunkts,
vor, d. h. hier
werden keine Resonanzschwingungen angeregt. Zwischen dem Intervall B und C, d.
h. unterhalb des Bifurkationspunkts, 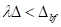 , liegt nur eine einzelne reelle stabile Wurzel mit
, liegt nur eine einzelne reelle stabile Wurzel mit 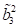 und eine instabile
Wurzel mit
und eine instabile
Wurzel mit 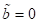 vor. Das sind die
Orte im Intervall BC mit den Frequenzen
vor. Das sind die
Orte im Intervall BC mit den Frequenzen 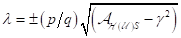 der b(
der b(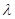 )- Kurve Am Bifurkationspunkt
)- Kurve Am Bifurkationspunkt 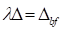 sowie links des
Punktes C, existieren alle drei reellen Amplitudenwerte, wobei die Wurzel
sowie links des
Punktes C, existieren alle drei reellen Amplitudenwerte, wobei die Wurzel 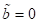 zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte die
den beiden stabilen Wurzeln bei
zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte die
den beiden stabilen Wurzeln bei 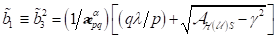 und
und 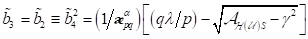 entsprechen mit deren
Frequenzen
entsprechen mit deren
Frequenzen 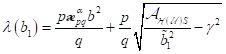 und
und 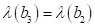 mit
mit 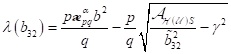 . Für jeden Wert des optischen Feldes oberhalb seines
Bifurkationspunktes
. Für jeden Wert des optischen Feldes oberhalb seines
Bifurkationspunktes 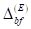 , ändert sich der Charakter der Resonanzerscheinungen. Der
Wert des Bifurkationspunktes entspricht genau dem Wendepunkt der Resonanzkurve.
Das ist derjenige Wert von E, bei dem beide reelle Wurzeln der in b2
quadratischen Gleichung mit
, ändert sich der Charakter der Resonanzerscheinungen. Der
Wert des Bifurkationspunktes entspricht genau dem Wendepunkt der Resonanzkurve.
Das ist derjenige Wert von E, bei dem beide reelle Wurzeln der in b2
quadratischen Gleichung mit 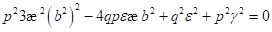 zusammenfallen, d. h.
an der Stelle E = Ek schrumpft der ganze Abschnitt CD auf einen
Wendepunkt zusammen. In Abhängigkeit der bestimmten Parameter b und λ
findet sich die Wurzel des Wendepunktes der Resonanzkurve mit:
zusammenfallen, d. h.
an der Stelle E = Ek schrumpft der ganze Abschnitt CD auf einen
Wendepunkt zusammen. In Abhängigkeit der bestimmten Parameter b und λ
findet sich die Wurzel des Wendepunktes der Resonanzkurve mit:
|
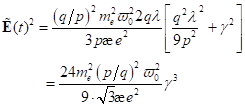
|
(87)
|
wobei sich
die speziellen Werte λ und b durch die verschwindende Diskriminante der in
b2 quadratischen Gleichung 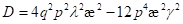 finden lassen. Damit
ergibt sich die kleine Variation λ zu
finden lassen. Damit
ergibt sich die kleine Variation λ zu 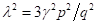 und die entsprechende
Wurzel kann mit
und die entsprechende
Wurzel kann mit 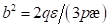 berücksichtigt werden.
Aufgrund des instabilen Zustands b=0, benötigt das NZS- System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Die erhaltenen
Formeln gelten nur im schmalen Intervall exakt resonanter Teilchen, d. h.
kleine
berücksichtigt werden.
Aufgrund des instabilen Zustands b=0, benötigt das NZS- System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Die erhaltenen
Formeln gelten nur im schmalen Intervall exakt resonanter Teilchen, d. h.
kleine 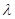 bzw.
bzw. 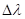 . Die Kleinheit von
. Die Kleinheit von 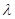 ist durch die
Kleinheit der Dämpfung
ist durch die
Kleinheit der Dämpfung 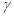 gewährleistet. Am
Bifurkationspunkt
gewährleistet. Am
Bifurkationspunkt 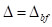 gibt es zwei stabile
Gleichgewichtspunkte, einer bei der Frequenz
gibt es zwei stabile
Gleichgewichtspunkte, einer bei der Frequenz 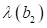 mit
mit 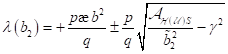 und ein weiterer bei
und ein weiterer bei 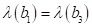 mit
mit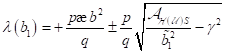 . Wie wir bereits in vorherigen Abschnitt zeigen konnten
lautet die Frequenz der kleinen Amplitude in der Umgebung eines stabilen
Fixpunkts
. Wie wir bereits in vorherigen Abschnitt zeigen konnten
lautet die Frequenz der kleinen Amplitude in der Umgebung eines stabilen
Fixpunkts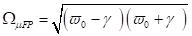 . Für die Nullfrequenz bei
. Für die Nullfrequenz bei 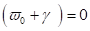 fallen die beiden
Wurzeln zusammen und der Fixpunkt wird instabil. Dies bewirkt ein
Hystereseverhalten. Abbildung 5 zeigt wie die Amplitudenvariation um die
stabilen Fixpunkte in Abhängigkeit des Verstimmungsparameters.
fallen die beiden
Wurzeln zusammen und der Fixpunkt wird instabil. Dies bewirkt ein
Hystereseverhalten. Abbildung 5 zeigt wie die Amplitudenvariation um die
stabilen Fixpunkte in Abhängigkeit des Verstimmungsparameters.
|
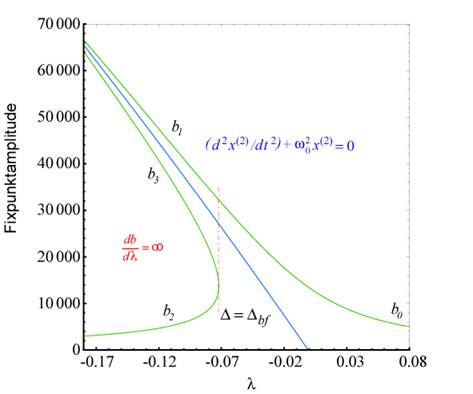
Abbildung 5 zeigt die Fixpunktentwicklung
nichtzentrosymmetrischer Medien mit quadratischer Nichtlinearität an der
Singularität in Abhängigkeit des Verstimmungsparameters λ. Wir erhalten
eine Resonanzkurve mit negativer Skewness die sich von links und rechts an
die Singularitätsstelle, die Skelettkurve (blau) anschmiegt; eE/me = 2 kV/m,
p=q=1, optische HeNe- Feldfrequenz ϖ = 2,9786 1/fs,
|
Der exakte
Verlauf des nichtlinearen optischen Responses nichtzentrosymmetrischer N.Z.-
und Z.-Symm- Materie im Fourierraum ergibt sich der Abhängigkeit zwischen der
Amplitude der stationären Schwingungen und der Erregerfrequenzen des optischen
Lichtfeldes.
|
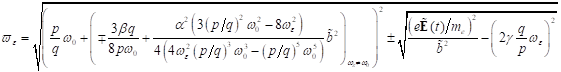
|
(88)
|
wobei die
nichtlineare ZS- und NZS Skelettkurve, d. h. der amplitudenabhängigen Korrektur
zur Resonanzfrequenz des Systems der Gleichung genügt:
|
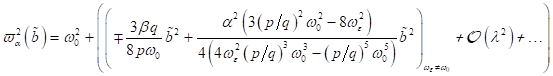
|
(89)
|
Da eine
quadratische Amplitudenabhängigkeit der Skelettkurve vorliegt, sind die
Frequenzwerte 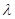 nicht eingeschränkt
und es finden für alle
nicht eingeschränkt
und es finden für alle 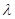 Schwingungen statt,
wobei für die Amplitude
Schwingungen statt,
wobei für die Amplitude 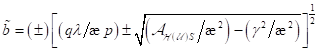 gilt. Ein weiteres
Ziel dieser Arbeit ist es, das exakte nichtlineare Verhalten des beleuchteten
Grenzflächenelektrons (Oberfläche) an der Resonanzstelle und deren Umgebung im
Fourierraum zu verstehen. Wir werden hier deshalb durch ein repräsentatives Beispiel
die sich daraus ergebenden speziellen Effekte zeigen, die Analytisch und
mithilfe der numerischen Integration gefunden wurden und vergleichen diese mit
den Lösungen, wie sie in der aktuellen Literatur [Boyd] publiziert sind.
Aufgrund der nichtlinearen Wechselwirkung des Teilchens mit hinreichend starken
externen optischen Feldern E > Ek ändert sich der Resonanzbeitrag
des Partikels im Fourierraum in Abhängigkeit der Frequenz. Wir verfolgen diese
Frequenzentwicklung und bestimmen die Änderung des Response- Beitrags. Zu
diesem Zweck werden wir in diesem Abschnitt die Bewegungsgleichung numerisch
integrieren und analytisch lösen. Die interessante Physik erhält man für
nichtlinear aktivierte Systeme d. h. α ≠ 0. Offensichtlich kippt die
Resonanzkurve bei hohen Anregungsamplituden weg, und wir sehen einen Sprung in
der Resonanzkurve. Die mathematische Lösungsstruktur ist in nachfolgender
Abbildung gezeigt. Es zeigt sich, dass Rechts vom Punkt B, d. h. oberhalb des
Bifurkationspunktes
gilt. Ein weiteres
Ziel dieser Arbeit ist es, das exakte nichtlineare Verhalten des beleuchteten
Grenzflächenelektrons (Oberfläche) an der Resonanzstelle und deren Umgebung im
Fourierraum zu verstehen. Wir werden hier deshalb durch ein repräsentatives Beispiel
die sich daraus ergebenden speziellen Effekte zeigen, die Analytisch und
mithilfe der numerischen Integration gefunden wurden und vergleichen diese mit
den Lösungen, wie sie in der aktuellen Literatur [Boyd] publiziert sind.
Aufgrund der nichtlinearen Wechselwirkung des Teilchens mit hinreichend starken
externen optischen Feldern E > Ek ändert sich der Resonanzbeitrag
des Partikels im Fourierraum in Abhängigkeit der Frequenz. Wir verfolgen diese
Frequenzentwicklung und bestimmen die Änderung des Response- Beitrags. Zu
diesem Zweck werden wir in diesem Abschnitt die Bewegungsgleichung numerisch
integrieren und analytisch lösen. Die interessante Physik erhält man für
nichtlinear aktivierte Systeme d. h. α ≠ 0. Offensichtlich kippt die
Resonanzkurve bei hohen Anregungsamplituden weg, und wir sehen einen Sprung in
der Resonanzkurve. Die mathematische Lösungsstruktur ist in nachfolgender
Abbildung gezeigt. Es zeigt sich, dass Rechts vom Punkt B, d. h. oberhalb des
Bifurkationspunktes 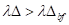 , nur eine verschwindende reelle Wurzel
, nur eine verschwindende reelle Wurzel 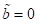 existiert und somit
keine Resonanzschwingungen erregbar sind.
existiert und somit
keine Resonanzschwingungen erregbar sind.
|
|
|
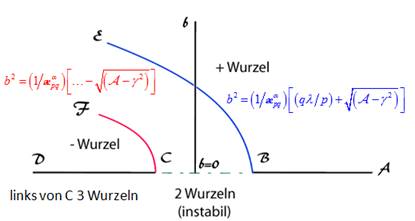
Abbildung 6: mathematische Lösungsstruktur
Zwischen dem
Intervall B und C, d. h. unterhalb des Bifurkationspunkts 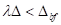 existiert nur eine einzelne reelle stabile Wurzel
existiert nur eine einzelne reelle stabile Wurzel 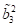 und die instabile
Wurzel
und die instabile
Wurzel 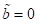 . Das sind die Orte im Intervall BC mit den Frequenzen
. Das sind die Orte im Intervall BC mit den Frequenzen 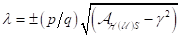 . Bewegt man sich
entlang des Astes BE so bewirkt die immer stärker einwirkende negative Wurzel
eine fortwährende Destabilisierung des oberen Astes bis die Amplitude unterhalb
des Abrißpunktes zusammenfällt.
. Bewegt man sich
entlang des Astes BE so bewirkt die immer stärker einwirkende negative Wurzel
eine fortwährende Destabilisierung des oberen Astes bis die Amplitude unterhalb
des Abrißpunktes zusammenfällt.
Die
numerisch erhaltene Amplitude nimmt von kleinen Frequenzwerten beginnend gemäß
dem harmonischen Ast zu bis in der Umgebung der Singularitätsstelle die
Amplitude auf den anharmonischen Ast springt und die Kurve über einen geringen
Unschärfebereich ausschmiert. Anschließend nimmt die Amplitude für höhere
Frequenzen entlang des anharmonischen Astes ab. Kommt man von hohen zu
niedrigen Frequenzen, nimmt die Amplitude gemäß dem anharmonischen Astes zu,
bis sie schließlich in der Umgebung der Singularitätsstelle abreißt und auf den
harmonischen Ast fällt und entlang dieser Kurve für abnehmende Frequenzen sich
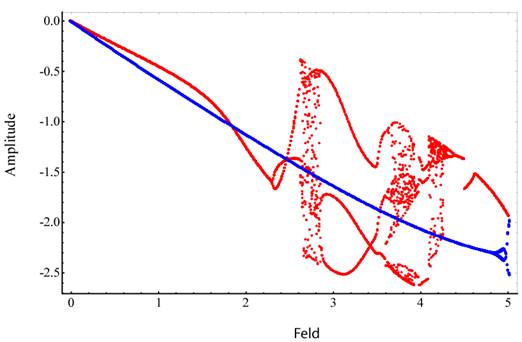
entsprechend verringert. In Abbildung 6 ist der Verlauf der Fixpunktamplitude
b(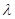 ) für NZS- Materie, charakterisiert durch
) für NZS- Materie, charakterisiert durch 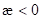 , grafisch dargestellt. Stabile Amplitudenbereiche ABC und
DEF werden vom Abrißpunkt B und dem Sprungpunkt D getrennt. Demnach gibt es
Abschnitte mit unstetigen Übergängen (gestrichelte Linie) und eine Hysterese,
wobei die beiden äußeren Äste stabil sind. Bei der Dipolemission muss daher
eine langsam veränderliche Amplitude auftreten, die von einer abrupten
Amplitudenänderung unterbrochen wird.
, grafisch dargestellt. Stabile Amplitudenbereiche ABC und
DEF werden vom Abrißpunkt B und dem Sprungpunkt D getrennt. Demnach gibt es
Abschnitte mit unstetigen Übergängen (gestrichelte Linie) und eine Hysterese,
wobei die beiden äußeren Äste stabil sind. Bei der Dipolemission muss daher
eine langsam veränderliche Amplitude auftreten, die von einer abrupten
Amplitudenänderung unterbrochen wird.
|
|
|
|
|
|
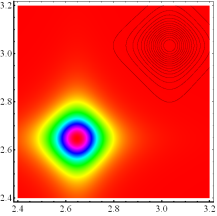
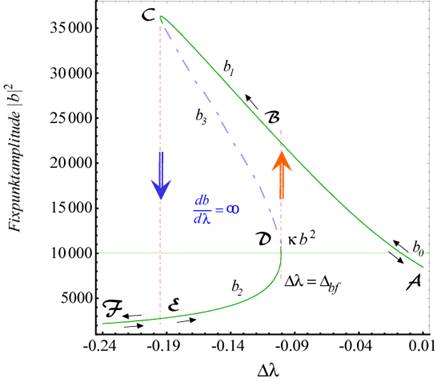
Abbildung 7 (oben) zeigt die Intensitätsdichteverteilung der Singularitätsstelle für die
Grundharmonische. Der Harmonische Response ist als Contour- Plot (oben rechts)
mit berücksichtigt. Die Abweichung vom harmonischen Response zeigt den Skew,
der nur im nichtlinearen Fall auftritt. Im Gegensatz zur Literatur- Lösung
[Boyd], in der die Nichtlinearität als Proportionalitätsfaktor berücksichtigt
wird und somit nur auf die Größe der Intensität Einfluss nimmt, kann mit der
hier erhaltenen Lösung und den entwickelten Programmen auch exakt die Skewness
der Amplitude bzw. Intensität vorhergesagt und beschrieben werden. (Unten) Verlauf der
Fixpunktentwicklungskurve b(λ) für 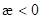 nichtzentrosymmetrischer Medien mit
quadratischer Nichtlinearität in Abhängigkeit des Verstimmungsparameters
λΔ. Wir erhalten eine optisch bistabile Resonanzkurve mit negativer
Skewness die Hystereseverhalten zeigt; eE/me = 2 kV/m, p=q=1,
optische HeNe- Feldfrequenz ϖ = 2,9786 1/fs,
nichtzentrosymmetrischer Medien mit
quadratischer Nichtlinearität in Abhängigkeit des Verstimmungsparameters
λΔ. Wir erhalten eine optisch bistabile Resonanzkurve mit negativer
Skewness die Hystereseverhalten zeigt; eE/me = 2 kV/m, p=q=1,
optische HeNe- Feldfrequenz ϖ = 2,9786 1/fs,
Die im
Fourierraum untersuchte analytische b(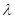 )- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysteresecharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" FED bis
zum Bifurkationswert
)- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysteresecharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" FED bis
zum Bifurkationswert 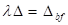 im Punkt D an, bei dem
eine vertikale Tangente erreicht wird mit
im Punkt D an, bei dem
eine vertikale Tangente erreicht wird mit 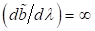 . Bei weiterer Erhöhung der Erregerfrequenzen springt die
Amplitude im Punkt D auf den Wert von Punkt B, d. h. es existiert nur noch eine
Lösung auf dem „oberen Ast“ mit negativer Tangente. Das System muss unstetig
auf diesen übergehen. Bei weiterer Erhöhung der Frequenz verringert sich die
Amplitude stetig entlang des "oberen Astes" BA. Verringert man jetzt
wieder die Frequenz so wächst die Amplitude entlang des oberen Astes A B bis
man zu C (bmax) kommt. Im Punkt C, unterhalb des
Bifurkationspunktes, reißt die Amplitude ab und sie fällt sprunghaft auf den
Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren Astes E
F der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte DC mit senkrechter Tangente
. Bei weiterer Erhöhung der Erregerfrequenzen springt die
Amplitude im Punkt D auf den Wert von Punkt B, d. h. es existiert nur noch eine
Lösung auf dem „oberen Ast“ mit negativer Tangente. Das System muss unstetig
auf diesen übergehen. Bei weiterer Erhöhung der Frequenz verringert sich die
Amplitude stetig entlang des "oberen Astes" BA. Verringert man jetzt
wieder die Frequenz so wächst die Amplitude entlang des oberen Astes A B bis
man zu C (bmax) kommt. Im Punkt C, unterhalb des
Bifurkationspunktes, reißt die Amplitude ab und sie fällt sprunghaft auf den
Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren Astes E
F der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte DC mit senkrechter Tangente 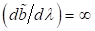 abgegrenzt.
abgegrenzt.
Die Bildung
des Differentialquotienten 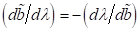 mit
mit 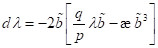 und
und 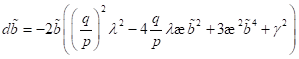 liefert:
liefert:
|
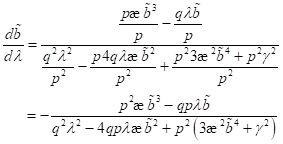
|
(90)
|
Daraus
ergeben sich die Orte der Punkte D und C aus den Singularitätsstellen mit 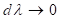 und
und 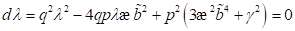 allgemein zu
allgemein zu 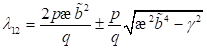 mit
mit 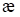 als nichtlinearen
Koeffizienten. Die Wurzel des Amplitudenmaximums (Punkt C) ergibt sich aus der
Bedingung
als nichtlinearen
Koeffizienten. Die Wurzel des Amplitudenmaximums (Punkt C) ergibt sich aus der
Bedingung 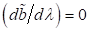 und kann gefunden
werden mit dem allgemeinen Ausdruck
und kann gefunden
werden mit dem allgemeinen Ausdruck 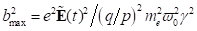 . Somit kann unter
Zuhilfenahme der numerischen und analytischen Lösung eindeutig eine negative
Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative Skewness
und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen, welche
nicht nur markant von den bisherigen Erkenntnissen für Oberflächen abweicht,
sondern sich auch vom Verhalten des Bulks sowie des Oberflächen / Bulks
Übergangs entsprechend ihrer positiven Skewness markant unterscheidet.
. Somit kann unter
Zuhilfenahme der numerischen und analytischen Lösung eindeutig eine negative
Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative Skewness
und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen, welche
nicht nur markant von den bisherigen Erkenntnissen für Oberflächen abweicht,
sondern sich auch vom Verhalten des Bulks sowie des Oberflächen / Bulks
Übergangs entsprechend ihrer positiven Skewness markant unterscheidet.
Neue subkritische
Bifurkation: In den nachfolgenden Abbildungen ist das Verhalten
zentro- nichtzentrosymmetrischer Materie oberhalb des Bifurkationspunkt
gezeigt. Dabei handelt es sich aus einer Kombination aus
Sattelpunktsbifurkation Turning- point Bifurkation, Subkritische und
superkritische Bifurkation.
Abbildung 8: Bifurkation nichtzentrosymmetrischer Materie.
Interessant ist die Lage der Fixpunkte in Abhängigkeit des
Nichtlinearitätsparameters α. Für negative α gabelt sich eine stabile
Gleichgewichtslage in einen stabilen und instabilen Zweig (Pendant zu b3)
auf, wobei dieses das Hystereseverhalten bewirkt. Für positive α
entsprechend umgekehrt, wobei dann entsprechend der untere Ast instabil wird.
Zentrosymmetrische Materie weist entsprechend in Abhängigkeit des
Nichtlinearitätsparameters β die zu NZS- Materie analoges
Bifurkationsverhalten auf. Der Unterschied liegt in der leichteren
Realisierbarkeit höherer Bifurkationspunkte im Bulk (unten: Bulk rot,
Oberfläche blau).
Wir
analysieren hier jetzt den nichtlinearen optischen Oberflächen- Response unter
Variation der Dämpfung und der Nichtlinearität. Dazu transformatieren wir
zuerst 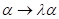 bzw.
bzw. 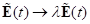 und
und 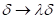 und erhalten:
und erhalten:
|
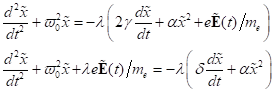
|
(91)
|
Weil (die
Resonanzfrequenz) 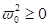 nur positiv oder
gleich Null sein kann, beschreibt der Response des stark nichtlinearen
Potentials die Materieantwort der Wechselwirkung mit einem hohen optischen Feld
und umgekehrt. Im folgenden finden wir näherungsweise eine sinusoidale Lösung
bei der Frequenz
nur positiv oder
gleich Null sein kann, beschreibt der Response des stark nichtlinearen
Potentials die Materieantwort der Wechselwirkung mit einem hohen optischen Feld
und umgekehrt. Im folgenden finden wir näherungsweise eine sinusoidale Lösung
bei der Frequenz  . Durch Analyse der Gleichgewichtspositionen kann die
Systemantwort eines periodischen optischen Feldes analysiert werden.
. Durch Analyse der Gleichgewichtspositionen kann die
Systemantwort eines periodischen optischen Feldes analysiert werden.
|

|
|
|
|
|
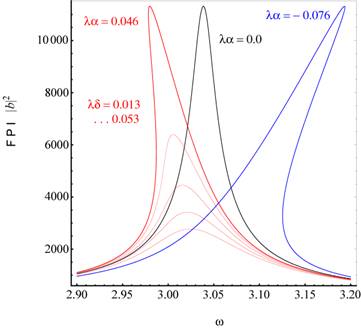
Abbildung 9 (oben) zeigt die nichtlineare
Intensitätsdichteverteilung an der Resonanzfrequenz für die Fundamentale. Der
harmonische Response ist zum Vergleich in der Mitte als Dichte- Plot mit
berücksichtigt. Die Abweichung vom harmonischen Response zeigt den Skew, der nur
im nichtlinearen Fall auftritt. Die Nichtlinearität durchläuft ein
vollständiges Vorzeichen und macht den Einfluss der Skewness deutlich sichtbar.
Für einen Vorzeichenwechsel der Nichtlinearität verschiebt sich das Maximum in
die entgegengesetzte Richtung (rechts oben). (Unten) Fixpunktentwicklung nichtzentrosymmetrischer N. Z. S.
Medien (rot), 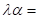 0.046165,
0.046165, 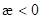 , mit behobener Singularität in Abhängigkeit der Variationen
, mit behobener Singularität in Abhängigkeit der Variationen 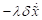 für die berechneten
Werte
für die berechneten
Werte 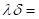 0.013 (Si- Kristall),
0.023, ... , 0.053. Für
0.013 (Si- Kristall),
0.023, ... , 0.053. Für 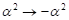 , d. h.
, d. h. 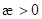 , erhalten wir eine vollständige Umkehr der Skewness wie sie
für zentrosymmetrische Materie und deren Übergang charakteristisch ist, siehe
weiter unten. Die blaue Kurve zeigt dies für den berechneten Wert
, erhalten wir eine vollständige Umkehr der Skewness wie sie
für zentrosymmetrische Materie und deren Übergang charakteristisch ist, siehe
weiter unten. Die blaue Kurve zeigt dies für den berechneten Wert 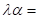 -0.076165 und
-0.076165 und 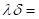 0.013. Zusätzlich
eingezeichnet ist der harmonische Fall kennzeichnend durch einen fehlenden Skew
0.013. Zusätzlich
eingezeichnet ist der harmonische Fall kennzeichnend durch einen fehlenden Skew
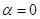 . Alle Kurven wurden mit den numerischen Eckparametern E =
0.3 kV/m, p=q=1, optische HeNe- Feldfrequenz ω = 2,9786 1/fs berechnet.
. Alle Kurven wurden mit den numerischen Eckparametern E =
0.3 kV/m, p=q=1, optische HeNe- Feldfrequenz ω = 2,9786 1/fs berechnet.
Für den Fall
vollständig fehlender Nichtlinearität (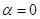 ) zeigt die Response Funktion im Fourierraum gewöhnliche
Resonanz bei
) zeigt die Response Funktion im Fourierraum gewöhnliche
Resonanz bei 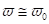 , wie sie charakteristisch für Lorentz- Materialien sind.
Unter Berücksichtigung quadratischer Nichtlinearität,
, wie sie charakteristisch für Lorentz- Materialien sind.
Unter Berücksichtigung quadratischer Nichtlinearität, 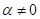 , zeigt sich ein Peak mit Skewness. Für
nichtzentrosymmetrische Materie mit
, zeigt sich ein Peak mit Skewness. Für
nichtzentrosymmetrische Materie mit 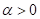 erhält man mit zunehmender
Amplitude eine harte Potentialcharakteristik und die Kurve zeigt negative
Skewness. Negative Nichtlinearität
erhält man mit zunehmender
Amplitude eine harte Potentialcharakteristik und die Kurve zeigt negative
Skewness. Negative Nichtlinearität 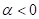 entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Abbildung 8 zeigt die
berechnete nichtlineare Response für reale Si- Kristalle an Oberflächen, Bulk
und deren Schnittstelle, sowie zu Vergleichszwecken deren Verhalten im linearen
Regime.
entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Abbildung 8 zeigt die
berechnete nichtlineare Response für reale Si- Kristalle an Oberflächen, Bulk
und deren Schnittstelle, sowie zu Vergleichszwecken deren Verhalten im linearen
Regime.
|
|
|
|
|
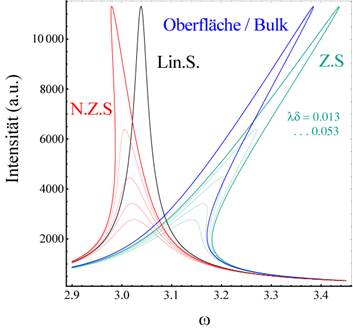
|
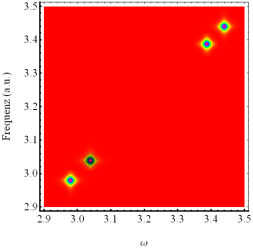
Abbildung 10 (oben): nichtlineare Intensitätsdichteverteilung an
der Singularitätsstelle in dissipativer Umgebung berechnet für NZS- ZS- Materie
und deren Oberfläche - Bulk Übergangsbereich. Der Harmonische Response ist als
Contour- Plot (Mitte) dem Dichte- Plot überlagert und ist kennzeichnend durch
einen fehlenden Skew  . Die Nichtlinearität durchläuft beim Übergang von
nichtzentrosymmetrischer Materie zu zentrosymmetrischer Materie über deren
Oberfläche / Bulk Übergang ein vollständiges Vorzeichen und macht den
Skewnesswechsel in Abhängigkeit der Materie deutlich sichtbar. (Unten) Nichtlineare
Fixpunktentwicklung nichtzentrosymmetrischer N. Z. S. Medien (rot),
. Die Nichtlinearität durchläuft beim Übergang von
nichtzentrosymmetrischer Materie zu zentrosymmetrischer Materie über deren
Oberfläche / Bulk Übergang ein vollständiges Vorzeichen und macht den
Skewnesswechsel in Abhängigkeit der Materie deutlich sichtbar. (Unten) Nichtlineare
Fixpunktentwicklung nichtzentrosymmetrischer N. Z. S. Medien (rot),  0.046165,
0.046165,  ,
, 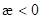 , mit behobener Singularität in Abhängigkeit der
Dissipationsvariation
, mit behobener Singularität in Abhängigkeit der
Dissipationsvariation 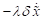 für die berechneten
Werte für reale Si- Kristalle
für die berechneten
Werte für reale Si- Kristalle 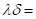 0.013 und in
hochdissipativer Umgebung
0.013 und in
hochdissipativer Umgebung 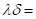 0.023, ... , 0.053. An
der Oberfläche / Bulk Schnittstelle ergeben sich durch Übergang auf 2
gegenwirkende Nichtlinearitäten, gemäß
0.023, ... , 0.053. An
der Oberfläche / Bulk Schnittstelle ergeben sich durch Übergang auf 2
gegenwirkende Nichtlinearitäten, gemäß 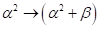 , mit der Oberfläche / Bulk Skewness von
, mit der Oberfläche / Bulk Skewness von 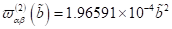 d. h.
d. h. 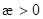 , nicht nur eine vollständige Kompensation der NZS- Skewness,
sondern vielmehr noch eine vollständige Umkehr der Skewness (blaue Kurve) wie
sie zudem in noch ausgeprägterer Form für zentrosymmetrische Materie (Bulk) mit
, nicht nur eine vollständige Kompensation der NZS- Skewness,
sondern vielmehr noch eine vollständige Umkehr der Skewness (blaue Kurve) wie
sie zudem in noch ausgeprägterer Form für zentrosymmetrische Materie (Bulk) mit
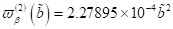 charakteristisch ist
(grüne Kurve). Die blaue Kurve zeigt dies für die Dissipation
charakteristisch ist
(grüne Kurve). Die blaue Kurve zeigt dies für die Dissipation 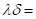 0.013 und für den Bulk
als grüne Kurve für die Dissipationen
0.013 und für den Bulk
als grüne Kurve für die Dissipationen 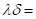 0.023, ... , 0.053.
Alle Kurven wurden mit den numerischen Eckparametern E = 0.3 kV/m, p=q=1,
optische HeNe- Feldfrequenz ω = 2,9786 1/fs berechnet.
0.023, ... , 0.053.
Alle Kurven wurden mit den numerischen Eckparametern E = 0.3 kV/m, p=q=1,
optische HeNe- Feldfrequenz ω = 2,9786 1/fs berechnet.
Abbildung 9
zeigt die Fixpunktintensität in Abhängigkeit von λΔ für drei verschiedene Verstimmungen ϖ∆
oberhalb des Bifurkationspunktes 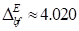 . Bemerkenswert ist in diesem Zusammenhang, dass eine
Erhöhung der Verstimmung eine Änderung der Skewness bewirkt, wie sie bislang
nur durch Vorzeichenwechsel der Nichtlinearität zu beobachten war.
. Bemerkenswert ist in diesem Zusammenhang, dass eine
Erhöhung der Verstimmung eine Änderung der Skewness bewirkt, wie sie bislang
nur durch Vorzeichenwechsel der Nichtlinearität zu beobachten war.
|
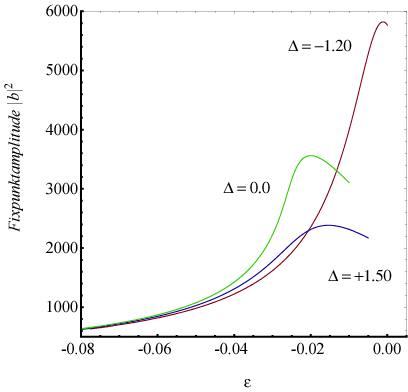
Abbildung 11 zeigt Fixpunktentwicklung nichtzentrosymmetrischer
Medien mit quadratischer Nichtlinearität in Abhängigkeit des
Verstimmungsparameters λΔ, e/meE=2.920596*100V/m.
|
Die
Untersuchung der Skewness hoher Harmonischer zeigt für jeweils 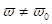 . eine Skewness welche sich in Abhängigkeit von der Ordnung
der Harmonischen ändert. Für hohe Harmonische konvergiert die Variation der
Skewness, wie aus nachfolgender Abbildung 11 ersichtlich ist.
. eine Skewness welche sich in Abhängigkeit von der Ordnung
der Harmonischen ändert. Für hohe Harmonische konvergiert die Variation der
Skewness, wie aus nachfolgender Abbildung 11 ersichtlich ist.
|
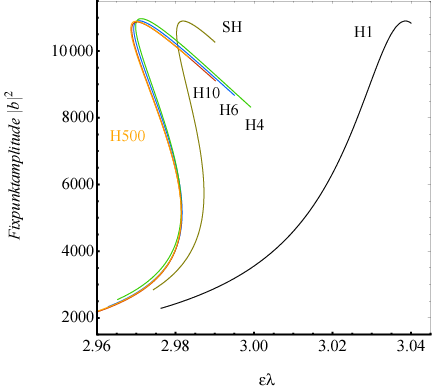
Abbildung 12 zeigt den Skew der Fixpunktentwicklung
nichtzentrosymmetrischer Medien mit quadratischer Nichtlinearität für
verschiedene Ordnungen der Harmonischen Generation in Abhängigkeit des
Verstimmungsparameters λΔ. Daraus ist ersichtlich, dass für hohe
Harmonische (H500) die Skew(ness) normalerweise konvergiert.
|
Abbildung 13 zeigt die Instabilitätsbereiche /
Stabilitätsbereiche gemäß der Singularitätsgleichung für die nichtlineare
Grundresonanz H2, H4, H6 (und die nächsten drei höheren geraden Harmonischen)
und die (Ultra-)Subharmonische mit mp/2, m=1 und 11 (rot) im extrem
nichtlinearen Regime mit α = +-20.165 . Es ist zu sehen, dass sich bei
vorhandener Dämpfung diese Bereiche mit zunehmender Ordnung der Harmonischen
verkleinern. Dies zeigt, dass die
höheren Harmonischen im nichtlinearen Regime mit zunehmender Ordnung immer
instabiler werden und immer schwerer zu realisieren sind. Damit sind
nichtlineare Schwingungen bei vorhandener Dämpfung die Grundresonanz ω0
 ν viel leichter bemerkbar zu machen als
es für die höheren Harmonischen pω0
ν viel leichter bemerkbar zu machen als
es für die höheren Harmonischen pω0  ν der Fall ist.
ν der Fall ist.
4. Literaturverzeichnis:
[SYR84] Shen, Y.
R. The Principles of Nonlinear Optics; Wiley: New York, 1984.
[Boyd] Boyd, R.
W. Nonlinear Optics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003.]
[PFTV92] W. H.
Press, B. P. Flannery, S. A. Teukolsky, und W. T. Vetterling, Numerical Recipes in C, 2nd ed., Press Syndicate of the University
of Cambridge, 1992.
Kombination von Theorie
und Praxis: Zum einen werden die numerischen Algorithmen vorgestellt und zum
anderen C- oder Fortran-Programme mitgegeben, die diese Algorithmen
implementieren.
[BSMM08] I. N.
Bronstein, K. A. Semendjajew, G. Musiol, H. Mühlig, Taschenbuch der
Mathematik, 7., vollständig überarbeitete und ergänzte Auflage, Verlag
Harri Deutsch, Frankfurt am Main, (2008)
[LL07- I] L. D. Landau und E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.I: Mechanik, 14., korrigierte Auflage, Akademie-Verlag, Berlin, (2007)
[LL09] L. D. Landau und E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.II: Klassische Feldtheorie, 12. Auflage, Akademie-Verlag, Berlin, (2009)
![]() zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte. Für
jeden Wert des optischen Feldes oberhalb seines Bifurkationspunktes, ändert
sich der Charakter der Resonanzerscheinungen. Der Wert des Bifurkationspunktes
entspricht dabei genau dem Wendepunkt der Resonanzkurve. Das ist derjenige Wert
von E, bei dem beide reelle Wurzeln der in b2 quadratischen
Gleichung zusammenfallen, d. h. an der Stelle E = Ek schrumpft der
ganze Abschnitt CD auf einen Wendepunkt zusammen. Aufgrund des instabilen
Zustands bei b=0 benötigt das nichtzentrosymmetrische System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Am
Bifurkationspunkt wurden zwei stabile Gleichgewichtspunkte identifiziert. Die
Frequenz der kleinen Amplitude in der Umgebung des stabilen Fixpunkts ergibt
sich zu
zu einer instabilen
Schwingungsform gehört, d. h. es existieren dort zwei Gleichgewichtspunkte. Für
jeden Wert des optischen Feldes oberhalb seines Bifurkationspunktes, ändert
sich der Charakter der Resonanzerscheinungen. Der Wert des Bifurkationspunktes
entspricht dabei genau dem Wendepunkt der Resonanzkurve. Das ist derjenige Wert
von E, bei dem beide reelle Wurzeln der in b2 quadratischen
Gleichung zusammenfallen, d. h. an der Stelle E = Ek schrumpft der
ganze Abschnitt CD auf einen Wendepunkt zusammen. Aufgrund des instabilen
Zustands bei b=0 benötigt das nichtzentrosymmetrische System keinen
„Anfangsstoß“ zur Erregung von Schwingungen, ganz im Gegensatz zu
zentrosymmetrischer Materie, wo ein „Anfangsstoß“ notwendig ist. Am
Bifurkationspunkt wurden zwei stabile Gleichgewichtspunkte identifiziert. Die
Frequenz der kleinen Amplitude in der Umgebung des stabilen Fixpunkts ergibt
sich zu ![]() . Für die Nullfrequenz fallen die beiden Wurzeln zusammen und
der Fixpunkt wird instabil. Dies liegt darin begründet, dass geringe
Dämpfungswerte
. Für die Nullfrequenz fallen die beiden Wurzeln zusammen und
der Fixpunkt wird instabil. Dies liegt darin begründet, dass geringe
Dämpfungswerte ![]() zu instabilen
Schwingungen führen. Dies bewirkt ein Hystereseverhalten. Offensichtlich kippt
die Resonanzkurve bei hohen Anregungsamplituden weg, und man erkennt einen
Sprung in der Resonanzkurve. Dabei zeigte sich, dass die numerischen Werte für
kleine Frequenzen sich entlang dem harmonischen Ast bewegen und für hohe
Frequenzen sich entlang dem anharmonischen Ast entwickeln. Dazwischen zeigt
sich eine Unschärfe im Hystereseverhalten in der Umgebung der
Singularitätsstelle mit verändertem Linienverlauf und veränderter Linienbreite.
Der numerisch erhaltene Response nichtzentrosymmetrischer Materie nimmt von
kleinen Frequenzwerten beginnend gemäß dem harmonischen Ast zu bis in der
Umgebung der Singularitätsstelle die Amplitude auf den anharmonischen Ast
springt und die Kurve über einen geringen Unschärfebereich ausschmiert.
Anschließend nimmt die Amplitude für höhere Frequenzen entlang des
anharmonischen Astes ab. Kommt man von hohen zu niedrigen Frequenzen, nimmt die
Amplitude gemäß dem anharmonischen Astes zu, bis sie schließlich in der
Umgebung der Singularitätsstelle abreißt, auf den harmonischen Ast fällt und
entlang dieser Kurve für abnehmende Frequenzen sich entsprechend verringert.
Die im Fourierraum untersuchte analytische b(
zu instabilen
Schwingungen führen. Dies bewirkt ein Hystereseverhalten. Offensichtlich kippt
die Resonanzkurve bei hohen Anregungsamplituden weg, und man erkennt einen
Sprung in der Resonanzkurve. Dabei zeigte sich, dass die numerischen Werte für
kleine Frequenzen sich entlang dem harmonischen Ast bewegen und für hohe
Frequenzen sich entlang dem anharmonischen Ast entwickeln. Dazwischen zeigt
sich eine Unschärfe im Hystereseverhalten in der Umgebung der
Singularitätsstelle mit verändertem Linienverlauf und veränderter Linienbreite.
Der numerisch erhaltene Response nichtzentrosymmetrischer Materie nimmt von
kleinen Frequenzwerten beginnend gemäß dem harmonischen Ast zu bis in der
Umgebung der Singularitätsstelle die Amplitude auf den anharmonischen Ast
springt und die Kurve über einen geringen Unschärfebereich ausschmiert.
Anschließend nimmt die Amplitude für höhere Frequenzen entlang des
anharmonischen Astes ab. Kommt man von hohen zu niedrigen Frequenzen, nimmt die
Amplitude gemäß dem anharmonischen Astes zu, bis sie schließlich in der
Umgebung der Singularitätsstelle abreißt, auf den harmonischen Ast fällt und
entlang dieser Kurve für abnehmende Frequenzen sich entsprechend verringert.
Die im Fourierraum untersuchte analytische b(![]() )- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysterescharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" bis zum
Bifurkationswert an, bei dem eine vertikale Tangente erreicht wird. Bei
weiterer Erhöhung der Erregerfrequenzen ändert sich die Amplitude sprunghaft,
d. h. es existiert nur noch eine Lösung auf dem „oberen Ast“ mit negativer Tangente.
Das System muss unstetig auf diesen übergehen. Bei weiterer Erhöhung der
Frequenz verringert sich die Amplitude stetig entlang des "oberen
Astes". Verringert man jetzt wieder die Frequenz so wächst die Amplitude
entlang des oberen Astes bis man zum Peakmaximum kommt. Unterhalb des
Bifurkationspunktes, reißt die Amplitude dann ab und sie fällt sprunghaft auf
den Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren
Astes der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte mit senkrechter Tangente abgegrenzt. Somit kann zusammenfassend
unter Zugrundelegung der numerischen und analytischen Lösung eindeutig eine
negative Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative
Skewness und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen,
welche nicht nur markant von den in der Literatur erforschten Erkenntnissen für
Oberflächen abweicht, sondern auch vom Verhalten des Bulks (mit
Ladungsunterschuss) sowie des Oberflächen / Bulks Übergangs entsprechend ihrer
positiven Skewness markant abweicht. Zudem wurde
das Modell soweit verfeinert, dass mit der hier erhaltenen Lösung und
den entwickelten Programmen auch exakt die Skewness der Amplitude bzw.
Intensität vorhergesagt und beschrieben werden kann. Dies stellt eine enorme
Verbesserung der bisherigen Modellbildung dar, in der die Nichtlinearität als
Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der
Intensität Einfluß nimmt. Die Analyse des nichtlinearen optischen Oberflächen-
Response unter Variation der Dämpfung und der Nichtlinearität ergab folgende
Erkenntnisse: Im Fall vollständig fehlender Nichtlinearität zeigt die Response
Funktion im Fourierraum gewöhnliche Resonanz bei
)- Kurve NZS- Systeme weist in Abhängigkeit der optischen
Erregerfrequenzen Schwingungen mit Hysterescharakter auf. Variiert man λ
von kleinen Werten beginnend nach höheren Erregerfrequenzen, so wächst die
Amplitude der erregten Schwingung entlang des "unteren Astes" bis zum
Bifurkationswert an, bei dem eine vertikale Tangente erreicht wird. Bei
weiterer Erhöhung der Erregerfrequenzen ändert sich die Amplitude sprunghaft,
d. h. es existiert nur noch eine Lösung auf dem „oberen Ast“ mit negativer Tangente.
Das System muss unstetig auf diesen übergehen. Bei weiterer Erhöhung der
Frequenz verringert sich die Amplitude stetig entlang des "oberen
Astes". Verringert man jetzt wieder die Frequenz so wächst die Amplitude
entlang des oberen Astes bis man zum Peakmaximum kommt. Unterhalb des
Bifurkationspunktes, reißt die Amplitude dann ab und sie fällt sprunghaft auf
den Wert von E und verläuft mit abnehmenden Frequenzen entlang des unteren
Astes der Resonanzkurve. Es gibt also unstetige Übergänge mit negativer Steigung
(gestrichelte Linie) und eine Hysterese. Der obere und untere Ast werden durch
die Punkte mit senkrechter Tangente abgegrenzt. Somit kann zusammenfassend
unter Zugrundelegung der numerischen und analytischen Lösung eindeutig eine
negative Skewness und Hystereseverhalten gezeigt werden. Damit ist die negative
Skewness und das Hystereseverhalten für NZS- Materie eindeutig nachgewiesen,
welche nicht nur markant von den in der Literatur erforschten Erkenntnissen für
Oberflächen abweicht, sondern auch vom Verhalten des Bulks (mit
Ladungsunterschuss) sowie des Oberflächen / Bulks Übergangs entsprechend ihrer
positiven Skewness markant abweicht. Zudem wurde
das Modell soweit verfeinert, dass mit der hier erhaltenen Lösung und
den entwickelten Programmen auch exakt die Skewness der Amplitude bzw.
Intensität vorhergesagt und beschrieben werden kann. Dies stellt eine enorme
Verbesserung der bisherigen Modellbildung dar, in der die Nichtlinearität als
Proportionalitätsfaktor berücksichtigt wird und somit nur auf die Größe der
Intensität Einfluß nimmt. Die Analyse des nichtlinearen optischen Oberflächen-
Response unter Variation der Dämpfung und der Nichtlinearität ergab folgende
Erkenntnisse: Im Fall vollständig fehlender Nichtlinearität zeigt die Response
Funktion im Fourierraum gewöhnliche Resonanz bei ![]() , wie sie charakteristisch für Lorentz- Materialien sind. Für
nichtzentrosymmetrische Materie mit
, wie sie charakteristisch für Lorentz- Materialien sind. Für
nichtzentrosymmetrische Materie mit ![]() erhält man mit
zunehmender (Feld-)Amplitude eine harte Potentialcharakteristik und die Kurve
zeigt negative Skewness. Negative Nichtlinearität
erhält man mit
zunehmender (Feld-)Amplitude eine harte Potentialcharakteristik und die Kurve
zeigt negative Skewness. Negative Nichtlinearität ![]() entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Bemerkenswert ist in
diesem Zusammenhang, dass oberhalb des Bifurkationspunktes, eine Erhöhung der
Verstimmung, eine Änderung der Skewness bewirkt, wie sie bislang nur durch
Vorzeichenwechsel der Nichtlinearität zu beobachten war. Die Untersuchung der
Skewness hoher Harmonischer zeigte, eine Skewness welche sich in Abhängigkeit
von der Ordnung der Harmonischen ändert. Für hohe Harmonische konvergiert die
Variation der Skewness. Eine Neue subkritische Bifurkation wurde identifiziert
und eine erweiterte genaue mathematische Lösungsstruktur wurde angegeben.
entspricht einer immer
weicher werdenden Feder und bewirkt einen positiven Skew. Bemerkenswert ist in
diesem Zusammenhang, dass oberhalb des Bifurkationspunktes, eine Erhöhung der
Verstimmung, eine Änderung der Skewness bewirkt, wie sie bislang nur durch
Vorzeichenwechsel der Nichtlinearität zu beobachten war. Die Untersuchung der
Skewness hoher Harmonischer zeigte, eine Skewness welche sich in Abhängigkeit
von der Ordnung der Harmonischen ändert. Für hohe Harmonische konvergiert die
Variation der Skewness. Eine Neue subkritische Bifurkation wurde identifiziert
und eine erweiterte genaue mathematische Lösungsstruktur wurde angegeben. ![]() in ein System
gekoppelter Differentialgleichungen 1. Ordnung umzuschreiben.
in ein System
gekoppelter Differentialgleichungen 1. Ordnung umzuschreiben.![]() und den Definitionen
und den Definitionen ![]() und
und ![]() mit
mit ![]() , wobei
, wobei ![]() der Phasenraum ist.
Damit konstruieren wir verschiedene Bilder ebener Phasentrajektorien für
ausgewählte Energiewerte. Es werden folgende Fälle betrachtet:
der Phasenraum ist.
Damit konstruieren wir verschiedene Bilder ebener Phasentrajektorien für
ausgewählte Energiewerte. Es werden folgende Fälle betrachtet:![]()
![]() und äußerster Fixpunkt
und äußerster Fixpunkt
![]() werden untersucht.
Dieser äußerste Fixpunkt wird in der Phasentrajektorie nicht mehr erreicht,
weil er ein instabiler Fixpunkt ist und dieser sich in der Umgebung der
Singularität befindet. Dies ist nicht mehr simulierbar und wird erreicht für
werden untersucht.
Dieser äußerste Fixpunkt wird in der Phasentrajektorie nicht mehr erreicht,
weil er ein instabiler Fixpunkt ist und dieser sich in der Umgebung der
Singularität befindet. Dies ist nicht mehr simulierbar und wird erreicht für ![]() . Die optische Feldstärke nimmt ihren Maximalwert Emax
am Fixpunkt
. Die optische Feldstärke nimmt ihren Maximalwert Emax
am Fixpunkt ![]() an. Am Ursprung
(zentraler Fixpunkt) des Phasendiagramms verschwindet das optische Feld.
Abbildung (1) zeigt einen Satz von Trajektorien in der (
an. Am Ursprung
(zentraler Fixpunkt) des Phasendiagramms verschwindet das optische Feld.
Abbildung (1) zeigt einen Satz von Trajektorien in der (![]() )- Phasenebene für einige ausgewählte Energiewerte bei
konstanter Verstimmung
)- Phasenebene für einige ausgewählte Energiewerte bei
konstanter Verstimmung ![]() weit unterhalb vom
Bifurkationswert
weit unterhalb vom
Bifurkationswert ![]() und deren sukzessive
Approximation in die Nähe des Bifurkationswerts. Abbildung (2) zeigt denselben
Satz von Energie Phasenkurven, diesmal aber für den konstanten Verstimmungwert
und deren sukzessive
Approximation in die Nähe des Bifurkationswerts. Abbildung (2) zeigt denselben
Satz von Energie Phasenkurven, diesmal aber für den konstanten Verstimmungwert ![]() .
.![]() :
: 
![]() )- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=
-0.10, α= 0.046165, E= 0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E = 4.020
(rote Kurve, zeigt den Beginn der Periodenverdoppelung). Die Fixpunkte liegen
bei
)- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=
-0.10, α= 0.046165, E= 0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E = 4.020
(rote Kurve, zeigt den Beginn der Periodenverdoppelung). Die Fixpunkte liegen
bei ![]() und
und ![]() .
.![]() :
:
![]() ,
, ![]() )- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=+2.25,
α= 0.046165, E=0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E=3.6826 (blaue
Kurve, Anfang Periodenverdoppelung). Die Fixpunkte liegen bei
)- Phasenraum für eine
Verstimmung (Energievariation) unterhalb des Bifurkationspunkts; ∆=+2.25,
α= 0.046165, E=0.1, 0.7, 1.5, 2.25, 3.0, (eine Periode), E=3.6826 (blaue
Kurve, Anfang Periodenverdoppelung). Die Fixpunkte liegen bei ![]() und
und ![]() . Hierbei wurde über 8 Perioden integriert
(dicke blaue Kurve) um deren zeitliche Stabilität zu zeigen.
. Hierbei wurde über 8 Perioden integriert
(dicke blaue Kurve) um deren zeitliche Stabilität zu zeigen.![]() ,0) begrenzt ist und einen homoklinischen loop bildet. In den
höheren Energie- Bereichen, d. h. höherer Beschleunigung des Treiberfeldes,
gibt es einen weiteren Satz von Kurven mit zunehmenden Amplituden, die bis
außerhalb des homoklinischen Loops reichen und die Zunahme des relativen
Anteils der höheren Harmonischen impliziert.
,0) begrenzt ist und einen homoklinischen loop bildet. In den
höheren Energie- Bereichen, d. h. höherer Beschleunigung des Treiberfeldes,
gibt es einen weiteren Satz von Kurven mit zunehmenden Amplituden, die bis
außerhalb des homoklinischen Loops reichen und die Zunahme des relativen
Anteils der höheren Harmonischen impliziert. ![]()
![]() ,
,![]() und der instabile
Fixpunkt mit einer Amplitude
und der instabile
Fixpunkt mit einer Amplitude ![]() geordnet werden in der
Reihe,
geordnet werden in der
Reihe,![]() . Die dazu korrespondierenden optischen Energien folgen der
Reihe
. Die dazu korrespondierenden optischen Energien folgen der
Reihe ![]() . Bemerkenswert ist, dass die optische Energie ein globales
Maximum beim stabilen Fixpunkt
. Bemerkenswert ist, dass die optische Energie ein globales
Maximum beim stabilen Fixpunkt ![]() hat und nicht
linksseitig begrenzt ist, wobei die linkseitige Ausprägung von der negativen
Skewness herrührt. Der harmonische Fall ist dagegen links- und rechtsseitig
begrenzt. Im Limes
hat und nicht
linksseitig begrenzt ist, wobei die linkseitige Ausprägung von der negativen
Skewness herrührt. Der harmonische Fall ist dagegen links- und rechtsseitig
begrenzt. Im Limes ![]() geht die optische
Energie über von
geht die optische
Energie über von ![]() und die Amplituden der
entsprechenden Fixpunkte nähern sich einander an. Für Energiewerte im Bereich
und die Amplituden der
entsprechenden Fixpunkte nähern sich einander an. Für Energiewerte im Bereich ![]() bzw.
bzw. ![]() , gibt es eine zweifache Degeneration der Kurve(n). Dies
tritt ein weil wenn wir vom instabilen Fixpunkt mit Amplitude
, gibt es eine zweifache Degeneration der Kurve(n). Dies
tritt ein weil wenn wir vom instabilen Fixpunkt mit Amplitude ![]() weggehen und nach
positiven x- Werten fortsetzen, die Energie zunächst abnimmt ohne am Wert
weggehen und nach
positiven x- Werten fortsetzen, die Energie zunächst abnimmt ohne am Wert ![]() gebunden zu sein und
durch diesen begrenzt zu werden. Währenddessen, wenn wir nach negativen x-
Werten fortfahren, nimmt ab dem Degenerationspunkt die Energie bis zum Maximum
bei
gebunden zu sein und
durch diesen begrenzt zu werden. Währenddessen, wenn wir nach negativen x-
Werten fortfahren, nimmt ab dem Degenerationspunkt die Energie bis zum Maximum
bei ![]() beim stabilen Fixpunkt
beim stabilen Fixpunkt
![]() schnell zu, um bei
noch negativeren x- Werten die Energie schnell wieder auf ein Minimum bei
schnell zu, um bei
noch negativeren x- Werten die Energie schnell wieder auf ein Minimum bei ![]() beim stabilen Fixpunkt
beim stabilen Fixpunkt
![]() abzugeben. Die
Abbildungen (3) und (4) zeigen die optischen Feldkonturen oberhalb des
Bifurkationspunktes
abzugeben. Die
Abbildungen (3) und (4) zeigen die optischen Feldkonturen oberhalb des
Bifurkationspunktes ![]() für die
Verstimmungswerte ∆= +2.25 und ∆= -0.1. Für hohe Verstimmungswerte,
wie sie für maximale Spinströme und deren Umgebung auftreten, gibt es zwei
relativ kleine Amplitudenbewegungen um den stabilen Fixpunkt (
für die
Verstimmungswerte ∆= +2.25 und ∆= -0.1. Für hohe Verstimmungswerte,
wie sie für maximale Spinströme und deren Umgebung auftreten, gibt es zwei
relativ kleine Amplitudenbewegungen um den stabilen Fixpunkt (![]() ,0) herum und eine weitere große Amplitude die außerhalb des
homoklinischen Loops liegt bei (
,0) herum und eine weitere große Amplitude die außerhalb des
homoklinischen Loops liegt bei (![]() ,0). Insgesamt liegt eine Periodenverdoppelung vor,
,0). Insgesamt liegt eine Periodenverdoppelung vor, ![]() . Für niedrigere Verstimmungswerte gibt es zwei
Amplitudenbewegungen mit etwas unterschiedlichen Amplitudenausprägungen um den
stabilen Fixpunkt (
. Für niedrigere Verstimmungswerte gibt es zwei
Amplitudenbewegungen mit etwas unterschiedlichen Amplitudenausprägungen um den
stabilen Fixpunkt (![]() ,0) herum und bilden einen homoklinischen Loop der bis zum
Fixpunkt (
,0) herum und bilden einen homoklinischen Loop der bis zum
Fixpunkt (![]() ,0) reicht. Insgesamt liegt ebenfalls eine
Periodenverdoppelung vor,
,0) reicht. Insgesamt liegt ebenfalls eine
Periodenverdoppelung vor, ![]() , welche aber in
diesem Fall niedrigerer Verstimmungswerte sich stärker ausgeprägt zeigt. Dies
beschreibt das Verhalten maximaler Ladungsströme und deren hinreichend kleiner
Umgebung um diese, welche eine ausgeprägte Degeneration der Amplitude und
Frequenzabhängigkeit verursacht. Letztendlich ergeben sich damit für Photo- und
Spinströme jeweils eine Aufspaltung des Phasenraums oberhalb des
Bifurkationspunktes, aber in unterschiedlicher Ausprägung. Dies führt zu einer
Degeneration und Skewness der Anregungsamplitude. Aus diesem Grund ist
gegenüber den Spinströmen eine leichtere und stärkere Photostromgeneration mit
höherer Reichweite zu erwarten.
, welche aber in
diesem Fall niedrigerer Verstimmungswerte sich stärker ausgeprägt zeigt. Dies
beschreibt das Verhalten maximaler Ladungsströme und deren hinreichend kleiner
Umgebung um diese, welche eine ausgeprägte Degeneration der Amplitude und
Frequenzabhängigkeit verursacht. Letztendlich ergeben sich damit für Photo- und
Spinströme jeweils eine Aufspaltung des Phasenraums oberhalb des
Bifurkationspunktes, aber in unterschiedlicher Ausprägung. Dies führt zu einer
Degeneration und Skewness der Anregungsamplitude. Aus diesem Grund ist
gegenüber den Spinströmen eine leichtere und stärkere Photostromgeneration mit
höherer Reichweite zu erwarten. 
![]() )- Phasenraum (Energievariation) oberhalb des
Bifurkationspunkts für eine Verstimmung ∆=+2.25; α= 0.046165,
E=3.7108 (blaue Kurve, Periodenverdoppelung) und für E= 4.3157 (rote Kurve,
eine Periode). Die Fixpunkte liegen bei
)- Phasenraum (Energievariation) oberhalb des
Bifurkationspunkts für eine Verstimmung ∆=+2.25; α= 0.046165,
E=3.7108 (blaue Kurve, Periodenverdoppelung) und für E= 4.3157 (rote Kurve,
eine Periode). Die Fixpunkte liegen bei ![]() und
und ![]() .
.
![]() )- Phasenraum für eine Verstimmung (Energievariation)
oberhalb des Bifurkationspunkts / -werts; α= 0.046165, ∆=-0.1,
E=4.18033 (rote Kurve, Periodenverdoppelung) und für E= 4.0 (schwarze Kurve,
eine Periode). Die Fixpunkte liegen bei
)- Phasenraum für eine Verstimmung (Energievariation)
oberhalb des Bifurkationspunkts / -werts; α= 0.046165, ∆=-0.1,
E=4.18033 (rote Kurve, Periodenverdoppelung) und für E= 4.0 (schwarze Kurve,
eine Periode). Die Fixpunkte liegen bei ![]() und
und ![]() .
.