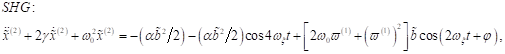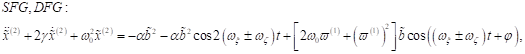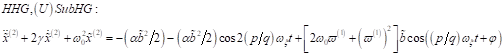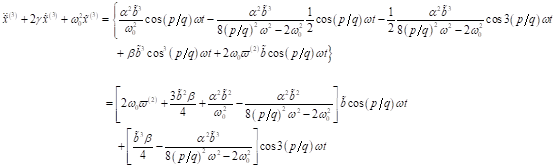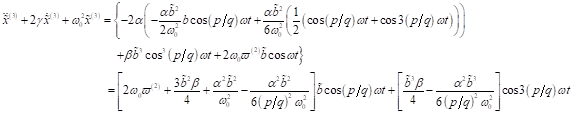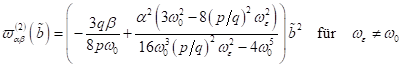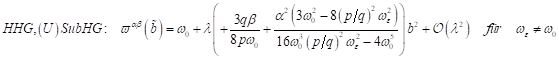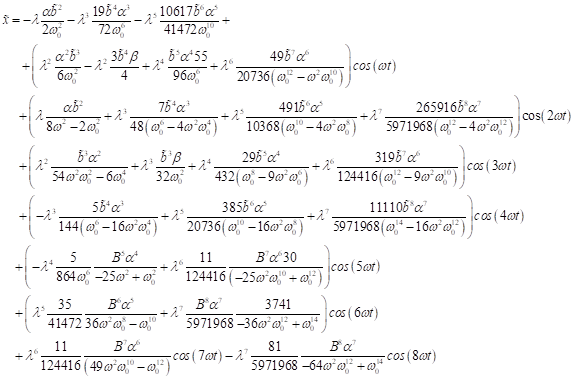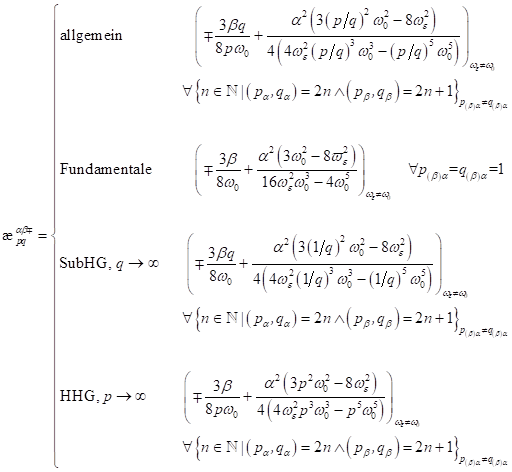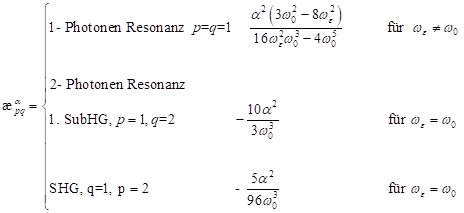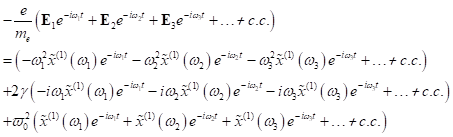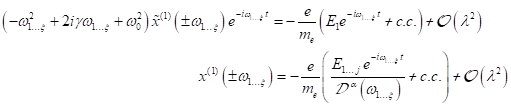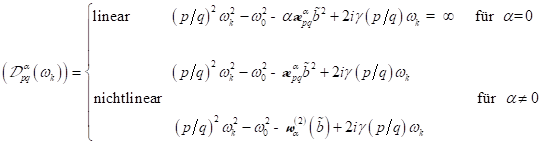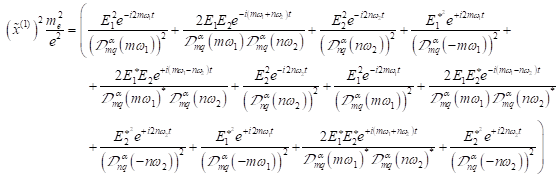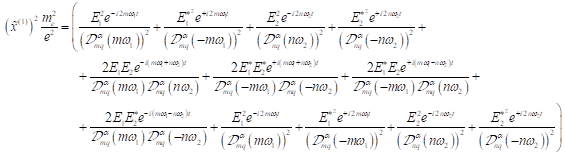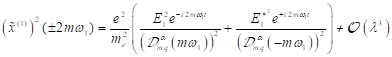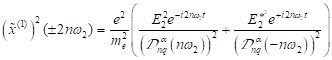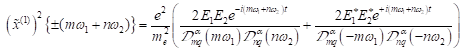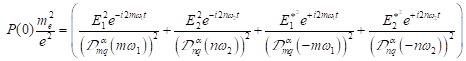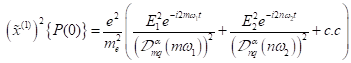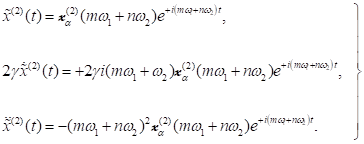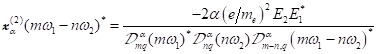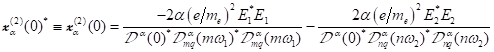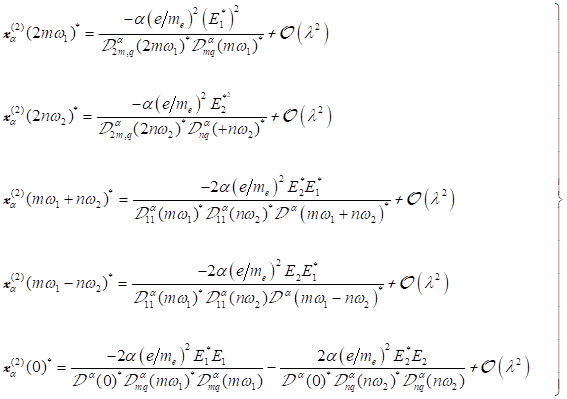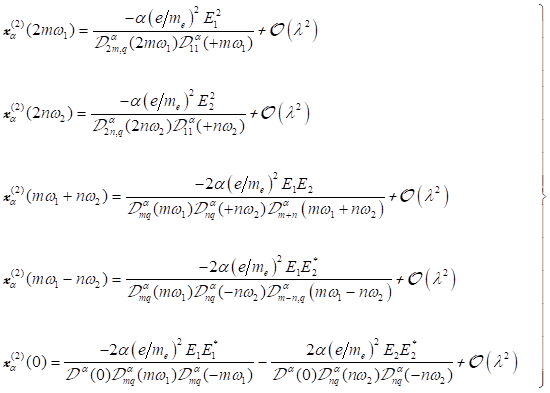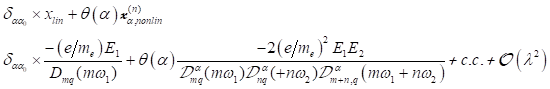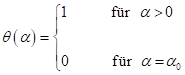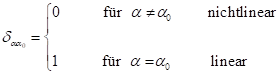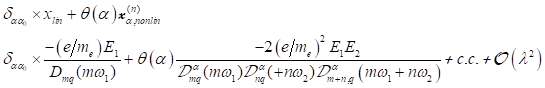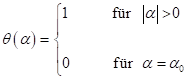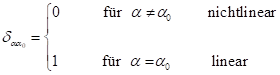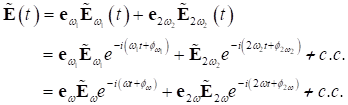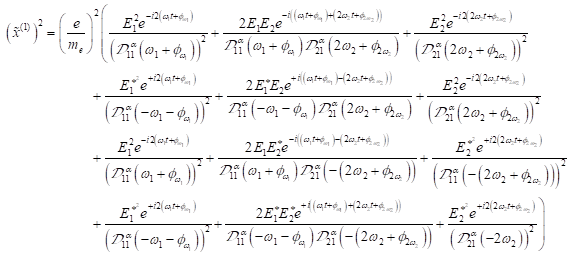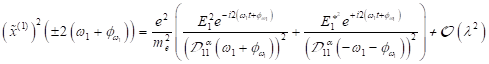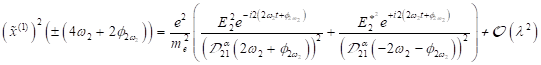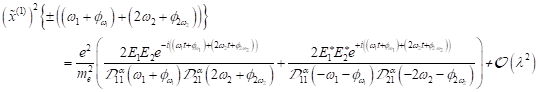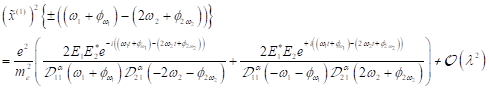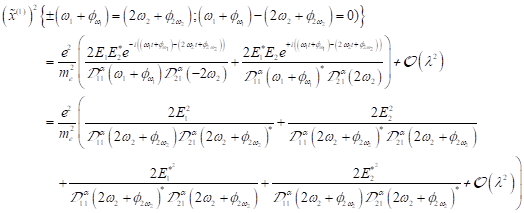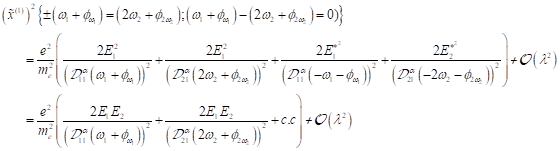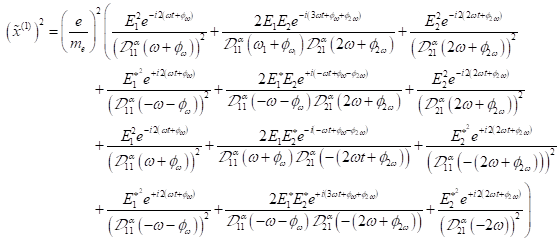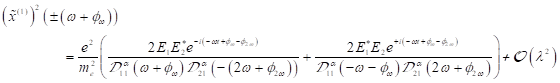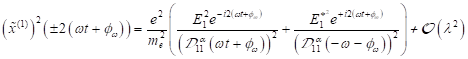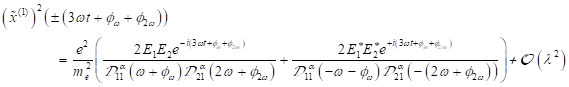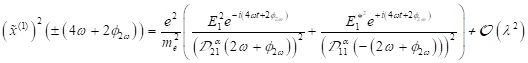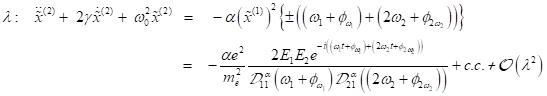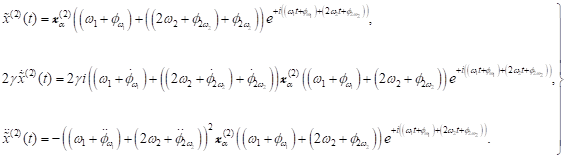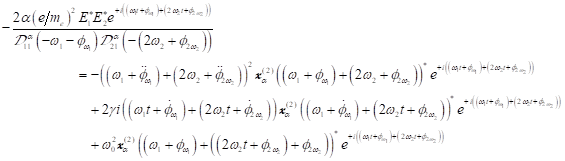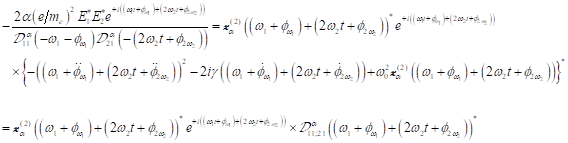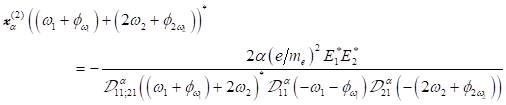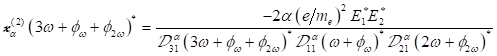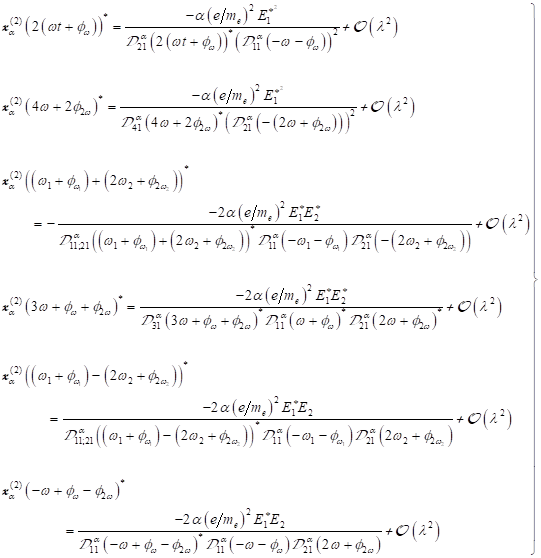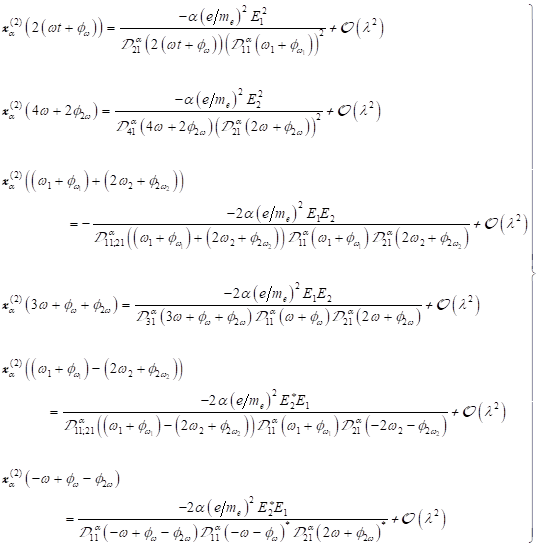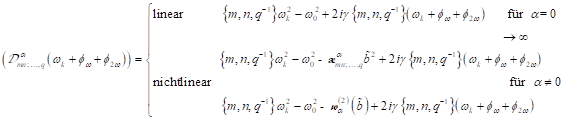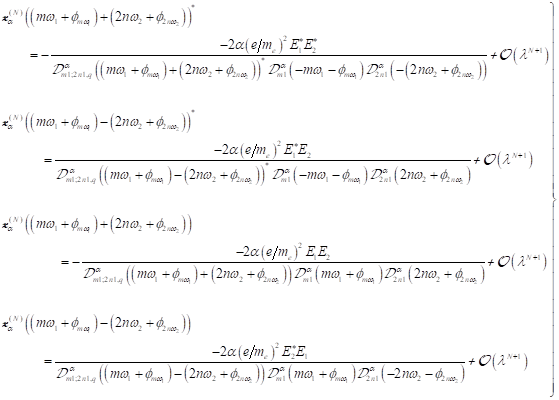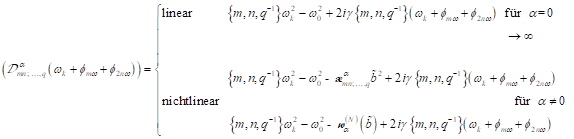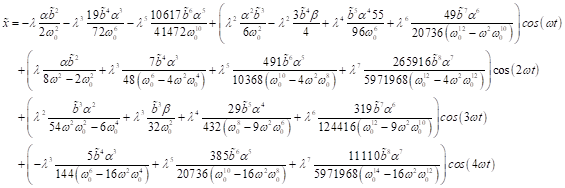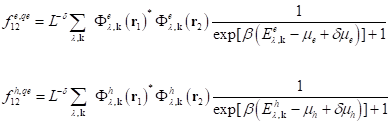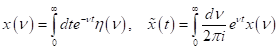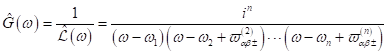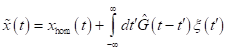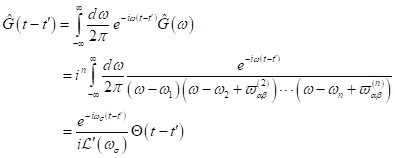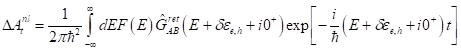Extreme nichtlineare Fourier- Optik:
Singularitäten hoher Harmonischer (HHG) und
Ultra-
Subharmonischer ((U)SubHG) unter dem Aspekt der kohärenten Erzeugung, Kinetik
und Kontrolle von Photo- und Spinströmen in Abhängigkeit der Materiesymmetrie
P. Krampl*
1. Einführung: Für ein monochromatisches Feld 
ist für
zentrosymmetrische Materie ein Skewnesseffekt bekannt und in der Literatur
illustriert (siehe z. B. [Landau]). Für multichromatische Felder und deren
komplex konjugierte ist eine harmonisch approximierte Lösung bekannt (siehe z.
B. [Boyd]). Diese Lösung ist nur gültig für genügend schwache optische Felder
wo die tatsächliche rücktreibende Kraft, die ein Oberflächenelektron für
genügend kleine Oszillationen um den Gleichgewichtszustand erfährt, durch ein
harmonisches Potential approximiert werden kann. Wird die Intensität des
eingestrahlten optischen Feldes groß, werden die höheren Terme der
Rückstellkraft wichtig und die Bewegung des Elektrons ist nicht länger direkt
proportional zum Feld. Nur in dieser Einschränkung kann das Langzeitverhalten
des nichtzentrosymmetrisch gebundenen Partikels störungstheoretisch
approximiert werden. Durch Vielwellenmischen oder Einstrahlung mehrerer höherer
Harmonischer und Kombinationen davon werden aber schnell hohe Felder erreicht.
Für diese Probleme müssen neue Strategien entwickelt werden. In dieser Arbeit
wird zunächst vorrangig die Wechselwirkung nichtzentrosymmetrischer Systeme mit
höheren bichromatischen photonischen Feldern der Form 
unter dem Aspekt der
Erweiterung auf höhere Harmonischen untersucht. Dies ist wichtig zur
Beschreibung der Erzeugung Dynamik von Photo- und Spinströmen.
Eine genaue
Untersuchung des Mechanismus zur exakten Beschreibung der Elektron-
Multiphotonenwechselwirkung wurde erstmals in meiner "Master´s Dissertation"
[PKM] als Ergebnis meines Studiums an der FU
Hagen dargestellt. Diese Lösungsstrukturen werden zunächst aufgegriffen und
danach erweitert. Im zweiten Teil dieser Arbeit werden die erweiterten
Ergebnisse zur Charakterisierung optisch kohärent induzierter und kohärent
kontrollierter Photo- und Spinströme verwendet. Zudem werden neue Ergebnisse
über die genauen physikalischen Vorgänge vom "Fermi- Gas" zur
"Fermi- Flüssigkeit" als Phasenübergang erster Ordnung hin zur
Umordnung zum entropieärmeren Festkörper als Phasenübergang zweiter Ordnung
gezeigt, die mit einer speziellen, nichtlinearen Änderung des chemischen
Potentials einhergeht. Zur Untersuchung des Langzeitverhaltens der Elektronen-
Multiphotonenwechselwirkung wird zunächst ein beliebig kleiner, positiver Störparameter
λ eingeführt. Das Ziel am Ende der Berechnung ist λ mit einem Wert
gleich eins zu besetzen.
|
|
(1) |
wobei 
ist, aber mit globalem 
in 
definiert ist und 
in dissipativer Umgebung. Die nichtlinearen
Parameter 
sind für Gase, Flüssigkeiten und kondensierte
Materie klein. Der Treiberterm 
mit dem photonischen multichromatischen Feld 
ist hierbei eine 
Funktion mit 2π- Periodizität. Für dieses Problem
ist bislang keine allgemeingültige analytische Lösung bekannt. Ein erster
analytischer Lösungsansatz für 2- Photonen- Resonanz und 3- Photonen Resonanz,
mit ersten Bezug auf beliebige Kombinationen höherer photonischer Fourierkomponenten,
wurde in meiner "Master´s Dissertation" [PKM] gezeigt. Die spezielle
Problematik hierbei ist, dass die Felder der auf die Kristalloberfläche
einfallenden Welle, welche von 2 getrennten photonischen Quellen herrühren
dabei nicht mehr einfach der
Superposition zweier Wellen entsprechen. Um dieses nichtlineare Problem zu
lösen wird zunächst die asymptotische Lösungsstruktur mittels Singularitäten
bestimmt. Dazu werden zunächst photonenfreie Oberflächen untersucht. Bei
vollständigem Fehlen externer optischer Felder liegt eine regellose freie
thermische Bewegung des Elektronenpartikels vor. Exakt resonante Partikel 
sind entropiearm und
deren Verhalten ist zeitlich vorhersagbar. Diese bestimmen das
Langzeitverhalten der Materieelektronen.
2. Asymptotischer
Aufbau des Elektronenresponses hoher Harmonischer und Subharmonischer: Bei
vollständigem Fehlen externer optischer Felder liegt eine regellose freie
thermische Bewegung des Elektronenpartikels vor. Exakt resonante Partikel 
sind entropiearm und
deren Verhalten ist zeitlich vorhersagbar. Diese bestimmen das
Langzeitverhalten der Materieelektronen. Zur weiteren Untersuchung des
Langzeitverhaltens wird ein beliebig kleiner, positiver Störparameter λ
eingeführt. Die stationäre Amplitude der Oberflächenelektronen in zweiter
Näherung, d. h. mit einer Genauigkeit bis zu kleinen Größen der Ordnung λ3
wird bestimmt mit:
|
|
(2) |
Die
Funktionen 
und die Größen 
können mit folgenden
Gleichungssystem bestimmt werden.
|
|
(3) |
|
|
(4) |
|
|
(5) |
aus (3)
findet man mithilfe der Modifikation für hohe Harmonische 
mit n als Integer 
und 
insgesamt 
mit 
. Damit erhält man aus (4.38) den Ausdruck:
|
|
(6) |
wobei keine
Additionstheoreme möglich ist und sich 
aufhebt für 
. Damit gibt es keinen Elektronen- Skew in der linearen
Näherung nichtzentrosymmetrischer Materie. Bemerkenswert ist in diesem
Zusammenhang, dass für zentrosymmetrische Medien bereits in erster Näherung
kleiner Größen mit 
ein Skew mit 
nachgewiesen werden
kann. Wir setzen 
und erhalten:
|
|
(7) |
Aus der
asymptotischen Näherung stationärer Lösungen erhalten wir über die
Beziehungen 
und 
mit der Phasenänderung
und 
die lineare Lösung 
für 
. Dies entspricht einer allgemeinen Lösung mit den
Randbedingungen x0 = b0 und 
, d. h zur Zeit t = 0 liegt nur die maximale Auslenkung b
vor. Damit diese Lösung, die nichtlineare Bewegungsgleichung (1) in
dissipativer Umgebung streng erfüllt, muss diese umgeschrieben werden in die
Form:
|
|
(8) |
wobei die
Identität 
benutzt wurde.
Mithilfe der Ergebnisse der asymptotischen Methode können wir die
Frequenzabweichung vom linearen Verhalten bestimmen. In zweiter Näherung
kleiner Größen erhalten wir:
|
|
(9) |
Die
Berücksichtigung freier Elektronen in der sukzessiven Näherung 
und 
liefert mit 
und 
mit der
trigonometrischen Identität 
in der Näherung
kleiner Größen bis zweiter Ordnung für dichromatisches Feld für die Komponente
der ersten höheren Harmonischen und allgemein für HHG und ((U)SubHG):
|
|
(10) |
|
|
(11) |
|
|
(12) |
Zur
Realisierung höherer Harmonischer sind mindestens zwei optische Pumpquellen
zwingend notwendig. Die Einstrahlung einer einzigen Frequenz 
erzeugt nur eine
Resonanz bei 
. Bestrahlung des nichtzentrosymmetrischen Systems mit 2
Frequenzen 
mit 
erzeugt neben der
Hauptresonanz 
höhere Resonanzen bei 
und für 
Resonanzen bei 
und 
mit 
. Die o. g. inhomogene, lineare Gleichung wird für freie
Partikel unter der Bedingung für das Fehlen eines Resonanzgliedes auf der
rechten Seite integriert. Damit können wir 
Null setzen und die
Integration liefert mit 
für das konstante
Glied 
. Wenn die Lösung erster Ordnung ein sinnvoller Startpunkt
ist, dann führt unsere allgemeine Argumentation von vornherein in den
allgemeinen Ansatz 
für 
und 
zu setzen. Mit der obigen
Argumentation wird der durch die Integration entstehende sin- Term komplex und
berücksichtigt die Dämpfung bzw. Absorption 
und der cos- Term ist
Real und beschreibt die Amplitude. Mit diesen Annahmen erhalten wir als allgemeingültige
Lösung zweiter Näherung kleiner Größen für die resonante Umgebung 
und unter zusätzlicher
Berücksichtigung hoher Harmonischer und Subharmonischer und entsprechend 
insgesamt:
|
|
(13) |
|
|
(14) |
Die
Lösungsstruktur der Integration an der Resonanzfrequenz und deren Umgebung
ergibt jeweils Lösungen der Form 
bzw. für eingestrahlte
optische hohen Harmonischen (HHG) und (Ultra)Subharmonischen ((U)SubHG, 
, mit Berücksichtigung der Felder in Form 
. Nach Voraussetzung liegen die Photonenresonanzen, d. h.
allgemein die hohen Harmonischen und Subharmonischen hinreichend nahe bei der
natürlichen Resonanzfrequenz. Im Limes kann damit für die hohen Harmonischen
beim Übergang zum Resonanzgebiet
, für die optischen Frequenzen 
geschrieben werden.
Für das Integral 
ergibt sich ferner 
an der Resonanz. Damit
lassen sich sofort die wichtigen Beziehungen 
für die Betrachtung an
der Resonanzfrequenz motivieren. Die Berücksichtigung der nächsthöheren Ordnung
liefert mit der Lösung zweiter Näherung kleiner Größen die Frequenzkorrektur
zur natürlichen Frequenz des Systems. Mit der erweiterten sukzessiven Näherung 
und 
finden wir für die
dritte Näherung kleiner Größen 
die analytische Lösung
für nichtresonante Erregerfrequenzen:
|
|
(15) |
und für resonante
Erregerfrequenzen:
|
|
(16) |
Die
Korrektur zur Fundamentalen erhalten wir aus den Koeffizienten des
Resonanzterms welcher das nichtlineare Verhalten an der Oberfläche - Bulk - Schnittstelle
wiedergibt.
|
|
(17) |
Daraus lässt
sich leicht erkennen, dass zentrosymmetrische und nichtzentrosymmetrische
Materie einen negativen Skew aufweisen. Betrachtet man nun positiv dotierte
Bulkfestkörper (
), so genügt diese der modifizierten Differentialgleichung
zweiter Ordnung 
. Dabei wurde berücksichtigt, dass der Bulk mit Schnittstelle
nicht invariant ist unter der Transformation 
. Somit ergibt sich dieselbe Lösungsstruktur wie für den
undotierten Bulk, wobei nur noch die Inversion des Nichtlinearitätsparameters
bzw. der Frequenz
berücksichtigt werden muss. Damit erhält man zwei konkurrierende Skews des
elektronischen Response 
bezüglich 
mit
|
|
(18) |
Für
nichtzentrosymmetrische Medien ist die amplitudenabhängige Frequenzkorrektur
dem Quadrat der Schwingungsamplitude proportional und 
. Analog erhält man in 
für zentrosymmetrische
Medien (Bulk) mit 
eine Frequenzkorrektur
positiver Skewness, bzw. für dotiertes Volumenmaterial negative Skewness,
welche jeweils dem Quadrat der Schwingungsamplitude proportional sind. Für hohe
nichtlineare Näherungen bis zu kleinen Größen 7. Ordnung lassen sich insgesamt
folgende Korrekturfaktoren für erzeugte hohe Harmonische bestimmen:
|
|
(19) |
Damit lassen
sich sofort die Frequenzkorrekturen an Oberflächen und Bulkmaterialien
erzeugten hohen Harmonischen bestimmen.
3. Singularitäten: In diesem
Abschnitt werden die möglichen nichtlinearen Resonanzfälle NZS- und ZS- Materie
betrachtet. Nach Voraussetzung liegen die 1- bzw. 2- Photonenresonanz, d. h.
allgemein die höheren Harmonischen und Subharmonischen hinreichend nahe bei der
natürlichen Resonanzfrequenz. Im Limes ist 
, 
. Nach Setzen der Variablentransformation 
und 
, lassen sich allgemeingültige Ausdrücke für die
nichtlinearen Koeffizienten zentro- und nichtzentrosymmetrischer Materie über
deren Schnittstelle, in der Näherung kleiner Größen bis 2. Ordnung formulieren
gemäß:
|
|
(20) |
mit den
Skewnesskoeffizienten der Anharmonizität, 
, welche mit 
undotierten und mit 
positiv dotierten
Festkörperbulk berücksichtigt. Dabei ist zu beachten, dass für die
Anharmonizitätspaare im nichtlinearen Regime, 
, nichtzentrosymmetrische Materie an Singularitätsstellen
gerader Ordnung und undotierte bzw. negativ dotierte zentrosymmetrische Materie
an Singularitätsstellen ungerader Ordnung jeweils mit negativer Skewness
skaliert. Für positiv dotierte zentrosymmetrische Materialien sowie deren
Schnittstelle Oberfläche / Bulk ist zu berücksichtigen, dass die Nichtlinearität
ein vollständiges Vorzeichen durchläuft und sich demzufolge eine Skewnessumkehr
ergibt. Damit lässt sich die exakte Lösungsstruktur für die nichtlineare
Amplitude, Suszeptibilität bzw. Brechungsindex, sowie der nichtlinearen
Polarisation in den jeweiligen Näherungen finden. Dabei ist zu berücksichtigen,
dass 
mit einer Genauigkeit
von 
in die Berechnungen
mit eingeht. Somit kann man für die jeweilige Materiegeometrie, in der Näherung
kleiner Größen bis 2. Ordnung, gültig für Frequenzintervalle 
, den exakten Verlauf des nichtlinearen optischen Response
für beliebig hohe Harmonische und Subharmonische vorhersagen. Beispielsweise
für die betrachtete 1- Photonen und 2- Photonen Resonanz
nichtzentrosymmetrischer- Materie im Fourierraum lässt sich für 
mit der nichtlinearen
Skelettkurve 
exakt angeben, wobei
sich die nichtlinearen Responsekoeffizienten ergeben zu:
|
|
(21) |
Bemerkenswert
ist hierbei, dass für die hohen Harmonischen die Skewness immer mehr zunimmt,
ganz im Gegensatz zu den Subharmonischen deren Skewness- Betrag immer weiter
abnimmt. Diese Modellbildung stellt eine enorme Verbesserung des bisherigen
nichtlinearen Modells dar (siehe z. B. [BRW03, Kapitel 1]), in der die
Nichtlinearität nicht nur approximiert wurde, sondern in ihrem innersten Wesen
exakt mathematisch berücksichtigt wurde. Dabei wird die Transformation der
nichtlinearen Resonanzfunktion 
vorgeschlagen, wobei
zusätzlich berücksichtigt werden muss, dass 
bzw. 
wird. Dies ergibt
sich, wenn die exakt auftretenden Singularitäten in den störungstheoretischen
Berechnungen berücksichtigt werden. Dies lässt sich in den hohen Näherungen für
"rein erzeugte" hohe Harmonische hervorragend bestätigen. Die exakte
nichtlineare Amplitude lässt sich durch Störungsrechnung als modifizierten Satz
von Gleichungen in Abhängigkeit der jeweils zugrundeliegenden Materiesymmetrie
erhalten. Wie zuvor erwähnt, besteht das externe Feld aus N-
Fourierkomponenten, wobei aufgrund der Linearität der Gleichungen sich die
Gesamtlösung aus einer Summe von N- Lösungskomponenten zusammensetzt. Die
stationäre Lösung kann durch einen Fourieransatz beschrieben werden:
|
|
(22) |
mit 
für reelle Amplituden.
Berücksichtigung der Differentiationen nach der Zeit liefert:
|
|
(23) |
Einstrahlung
beliebiger Fourierkomponente 
getragen von nur einem
Feld unter Berücksichtigung ihrer komplex konjugierten 
und Vergleich der
Fourierkomponenten 
der l. S. und der r.
S. von Gleichung (23), ergibt Ausdrücke für die jeweilige Fourieramplitude 
welche lösbar ist mit
|
|
(24) |
mit der
komplexen resonanten Frequenzfunktion
, wohlgemerkt definiert auf die
tatsächlich im Spektrum auftretenden reziproken Frequenzen, für die
gilt:
|
|
(25) |
wobei 
im Resonanznenner,
aufgrund der Einbeziehung ihrer c. c. Felder, sowohl positiv als auch negativ
sein kann. Für nichtzentrosymmetrische Materie ergeben sich Elektronenresponses
gerader Ordnung. Im Fall von zwei Fourierkomponenten des Photonenfeldes gibt es
letztendlich Frequenzresponses gemäß der Summenfrequenz- und
Differenzfrequenzgeneration und einen Gleichanteil. Der SHG Response für
monochromatische photonische Felder kann unter Berücksichtigung der bestimmten
zeitlichen Entwicklung des Treiberterms 
durch Transformation
in den Fourierraum gelöst werden. Substitution von (22) in den Entwicklungsterm
1. nichtlinearer Ordnung der Störungsrechnung ergibt:
|
|
(26) |
Dazu muss in
dieser Gleichung der quadratische Treiberterm 
betrachtet werden. Die
Lösung liefert dann die entsprechenden neuen "exotischen"
Frequenzterme. Im Falle von 2 Fourierkomponenten und deren komplex konjugierten
des externen Photonenfeldes der Form 
kann man folgende zu
berücksichtigenden quadratischen Komponenten hinschreiben:
|
|
(27) |
Mathematische
Umformungen ergeben folgende Einzelkomponenten mit Exponentialtermen der Form 
, 
, 
, 
, 
:
Damit erhält
man:
|
|
(28) |
Zusammenfassung
und Vereinfachung liefern Exponentialterme der Form , , 
, 
|
|
(29) |
Sortieren
der einzelnen Fourierkomponenten und Klassifizierung der einzelnen Terme führt
neben den neuen Responses, bei der doppelten Frequenz ±2mω1, ±2nω2 auch noch
zu Summen- und Differenzenfrequenzen ±(mω1+nω2),
±(mω1−nω2) und einem Gleichanteil DC. Die
Fourier Amplitude x(2) setzt sich also aus der Summe all dieser
Komponenten zusammen.
|
|
(30) |
Damit können
die neuen Treiberterme mit einer Genauigkeit bis zu kleinen Größen zweiter
Ordnung 
in Abhängigkeit der
generierten Frequenzen angegeben werden:
Hohe Harmonische (HHG) 
, 
:
|
|
(31) |
|
|
(32) |
Summenfrequenzerzeugung (SFG) und
Differenzfrequenzerzeugung (DFG) 
|
|
(33) |
|
|
(34) |
Gleichanteil (DC):
|
|
(35) |
|
|
(36) |
Zur
Bestimmung des Summenresponse in 
mit den Frequenzen 
erhält man durch
Berücksichtigung der entsprechenden Frequenz- Treiberterme.
|
|
(37) |
Dabei
entspricht der für die positive Frequenzkomponente 
zu berücksichtigende
Treiberfeldterm 
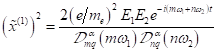, der komplex konjugierte Term 
den negativen
Fourierkomponenten 
. Die stationäre
Lösung für die Summenfrequenzerzeugung und deren zeitlichen Ableitungen für c.
c. Felder sind von der Form
|
|
(38) |
Substitution
von (38) in (37) ergibt für komplex konjugierte optische Felder:
|
|
(39) |
Elementare
mathematische Umformungen liefern einen Ausdruck, welcher für alle Zeiten t
erfüllt sein muss.
|
|
(40) |
Dies ist nur
der Fall, wenn der Klammerausdruck in (40), welcher der komplexen Frequenzfunktion
für Summenfrequenzerzeugung (SFG) entspricht, sich aufhebt. Damit ergibt sich
die Fourieramplitude für SFG zu:
|
|
(41) |
für
identische Frequenzen 
kann sofort auf die
negative Fourierkomponente der zweiten Harmonischen geschlossen werden. Für
leiche Amplitudenwerte lässt sich anschreiben:
|
|
(42) |
Analog zur
mathematischen Modellierung von SFG erhält man die Ausdrücke für die
Fourieramplitude für DFG 
für den negativen
Differenzfrequenzbereich 
zu:
|
|
(43) |
Werden
wiederum identische Frequenzen betrachtet so ergibt sich daraus der
Gleichanteil c. c. zu:
|
|
(44) |
Insgesamt
erhält man hiermit zwei Sätze von "exotischen" Ausdrücken zur
Beschreibung der Wechselwirkung von bichromatischem Licht mit
zentrosymmetrischer Materie, welche Singularitäten bzw. in dissipativer
Umgebung behobene Singularitäten bei den Frequenzen ±2ω1,
±2ω2, ±(ω1+ω2), ±(ω1−ω2)
generieren. Für die negativen Frequenzkomponenten läßt sich folgender Satz von
Gleichungen anschreiben
|
|
(45) |
bzw. ihrer
c. c. komplex konjugierten photonischen Felder für den positiven Frequenzbereich:
|
|
(46) |
mit der
exakten komplexen, nichtlinearen Resonanzfunktion:
|
|
(47) |
Die
nichtlineare Fourieramplitude Amplitude 
hoher Harmonischer und
(U)SubHG setzt sich aus der Summe all dieser Komponenten zusammen.
Bemerkenswert bei diesen Gleichungen ist, dass die Nichtlinearität in die
Frequenzfunktion im Nenner eingeht und nicht, wie in der aktuellen Literatur
(siehe z. B. [BRW03, Kapitel 1]), lediglich als Proportionalitätsfaktor, der
die Amplitude nur lorentzförmig beeinflusst. Zusätzlich muss für den
Nichtlinearitätsparameter mit 
berücksichtigt werden,
dass nichtzentrosymmetrische Materie nicht invariant ist unter der
Transformation 
. Dies impliziert die Tatsache, dass die Orientierung des
nichtlinearen Skewness- Effekts aufgrund der quadratischen Amplitudenabhängigkeit
für nichtzentrosymmetrische Materie rein frequenzabhängig ist. Damit kann ein
allgemeingültiger Ausdruck für die nichtlineare Elektron-
Multiphotonenwechselwirkung formuliert werden. Für nichtzentrosymmetrische
Materie ergibt sich insgesamt folgende allgemeine Lösung der Form:
|
|
(48) |
mit
|
|
(49) |
und
|
|
(50) |
wobei 
gilt. Für
zentrosymmetrische Materie kann nachfolgende allgemeine Lösung formuliert
werden:
|
|
(51) |
mit
|
|
(52) |
und
|
|
(53) |
Zur weiteren
Erforschung der nichtlinearen Materiewechselwirkung wird die mathematische
Struktur in der entwickelten Modellbildung betrachtet und deren berechnete
Konfiguration für die Untersuchung für den Hochforschungsbereich der Photo- und
Spinströme zugrundegelegt.
4. Photo- und
Spinströme: Die exakte nichtlineare Dynamik der
erzeugten Photo- und Spinströme, kann im Rahmen der klassischen Feldtheorie
durch die nichtlineare o. g. ODE () beschrieben werden. Es ist eine
nichtlineare Beschreibung notwendig, da man durch Multiwellenmischen, hier mit
2 Farben Anregung, sich im nichtlinearen Regime befindet. Im nichtlinearen
Regime sind die durch das Superpositionsprinzip bedingten (quantenmechanischen)
Interferenzphänomene nicht mehr so einfach wie in der linearen Theorie
handhabbar, da hier das Superpositionsprinzip verletzt ist. Diese müssen aber
berücksichtigt werden, da sie zur Steuerung und Kontrolle der Dynamik des
Nicht- Gleichgewichtsprozesses dient. Dieses nichtlineare System ist nur
numerisch lösbar und wird hier erstmals für dieses Problem exakt gelöst. Die
für die kohärente Erzeugung von Photo- und Spinströmen benötigten 2- Farben
Lichtfelder mit der Fundamentalfrequenz und der 2. Harmonischen besitzen die
Form:
|
|
(54) |
und für
kohärente HHG und (U)SubHG
|
|
(55) |
wobei m und
n für Integerwerte hohe Harmonische und Teilwerte von diesen (U)SubHG Felder
berücksichtigen, mit 
als die jetzt zu
berücksichtigenden Polarisationsrichtungen der optischen Felder zueinander. Für
, d. h. zwei
zueinander linear polarisierte parallele Pulse mit den Zentralfrequenzen der
Fundamentalen und 2. Harmonischen, ω und 2ω, (hohe harmonische und
(U)SubHG 
) werden Ladungsströme unter Nutzung von
Interferenzerscheinungen der Ein- und Zwei-Photonen-
Übergängen (bzw. m- und 2n- Übergänge) optisch erzeugt, anstatt durch
ein äußeres, schwaches, statisches Feld. Die Photostromgeneration und deren
Dynamik können im Rahmen der neuen Modellbildung unter Berücksichtigung
nichtlinearer Effekte beschrieben werden. Durch die parallele optische
Zwei-Puls-Anregung lassen sich Elektronverteilungen erzeugen, die im k-Raum
eine bestimmte Vorzugsrichtung aufweisen. Diese Verteilungen entsprechen einem
makroskopischen Ladungsstrom in positiver oder negativer Polarisationsrichtung
ganz unabhängig vom Spin. Das Vorzeichen des Stroms kann durch die Phase der
verwendeten Laserpulse gesteuert werden. Es lassen sich durch modifizierte
Anregungsbedingungen in Form von gekreuzten kohärenten optischen Pulsen 
mit 
reine Spinströme ohne
zusätzliche Ladungsströme erhalten [nach R. D. R. Bhat und J. E. Sipe aus dem
Jahr 2000 ]. Nach dieser Anregungsform liegt
ein reiner Spintransport vor, ohne makroskopischen Ladungsstrom, da die zu den
Elektronen mit unterschiedlichem Spin gehörenden Verteilungen genau
entgegengesetzte Ströme erzeugen. Zunächst sollen die Betrachtungen auf
beliebige kohärente Fundamental und SHG- Anregungsfrequenzen ausgeweitet werden
um daraus die Photo- und Spinströme beschreiben zu können und relevante
Unterschiede erkennen zu können. Es ergeben sich für allgemeine
Anregungsfrequenzen der Form 
gemischte
Exponentialterme der Form 
, 
, 
, 
, 
. Daraus ergeben sich mit 
, 
, 
, 
Anregungen bei der
doppelten und vierfachen Frequenz und gemischte Summen- und
Differenzenfrequenzen. Nur noch für Frequenzen 
ergibt sich ein
Gleichanteil.
|
|
(56) |
Treiberterm Response von ω1
an 2. Harmonischen (SHG) 
:
|
|
(57) |
Treiberterm Response ω2
an 4. Harmonischen (FHG) 
:
|
|
(58) |
Treiberterm gemischte
Summenfrequenzanregung (gSFG) 
|
|
(59) |
Treiberterm gemischte
Differenzfrequenzanregung (gDFG) 
|
|
(60) |
Treiberterm Anregungsgleichanteil
(DC):
|
|
(61) |
|
|
(62) |
Die
Betrachtung der einhergehenden Entstehung und Dynamik von Photo- und
Spinströmen durch die Elektron- Photonen Wechselwirkung mit den
Einstrahlungsfrequenzen 
liefert
Exponentialkomponenten der Form 
, 
, 
, 
, 
. Somit erhält ein Spektrum für Photo- und Spinströme,
welches neben der Anregung an der Hauptresonanz noch neue Responses für
positive und negative doppelte, dreifache und vierfache Frequenzen mit
entsprechendem Phasenanteil, 
enthält. Der
Gleichanteil DC 0 verschwindet gänzlich. Damit lässt sich anschreiben:
|
|
(63) |
Die Fourier
Amplitude x(2) für die Dynamik der erzeugten Photo- und Spinströme
setzt sich also aus der Summe all dieser verbleibenden Komponenten zusammen.
Damit können die neuen Treiberterme der neuen Photo- und Spinstromanregungen
für die erzeugten Photo- und Spinströme mit einer Genauigkeit bis zu kleinen
Größen zweiter Ordnung 
in Abhängigkeit der
generierten Frequenzen 
, 
, 
, 
angegeben werden:
Fundamentalanregung:
|
|
(64) |
Treiberterm Photo- und Spinstrom-
Response von ω1 an 2. Harmonischen (SHG) 
:
|
|
(65) |
Treiberterm Photo- und Spinstrom-
Response von ω1 an dritter Harmonischen (THG) 
:
|
|
(66) |
Treiberterm Photo- und Spinstrom-
Response von ω1 an vierter Harmonischen (FHG) 
:
|
|
(67) |
Zur
Bestimmung des allgemeinen Summenresponse in mit den Frequenzen 
erhält man durch
Berücksichtigung der entsprechenden Frequenz- Treiberterme.
|
|
(68) |
Dabei
entspricht der für die positive Frequenzkomponente 
zu berücksichtigende
Treiberfeldterm 
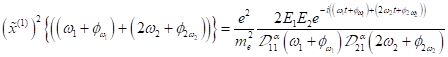, der komplex konjugierte Term 
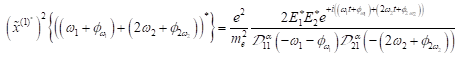den negativen
Fourierkomponenten 
. Die stationäre Lösung für die Summenfrequenzerzeugung und
deren zeitlichen Ableitungen für c. c. Felder sind von der Form:
|
|
(69) |
Substitution
von (69) in (68) ergibt für komplex konjugierte optische Felder:
|
|
(70) |
Mathematische
Umformungen liefern einen Ausdruck, welcher für alle Zeiten t erfüllt sein
muss.
|
|
(71) |
Dies ist nur
der Fall, wenn der Klammerausdruck in (71), welcher der nichtlinearen komplexen
Denominatorfunktion für gemischte Summenfrequenzerzeugung (gSFG) entspricht,
sich aufhebt. Damit ergibt sich die Fourieramplitude für gSFG zu:
|
|
(72) |
Für
identische Frequenzen 
kann sofort auf die
negative und alle weiteren Fourierkomponenten der Anregung der der Photo- und
Spinströme in Form der Fundamentalen und zweiten Harmonischen geschlossen
werden.
|
|
(73) |
Insgesamt
erhält man hiermit zwei Sätze von neuen "exotischen" Ausdrücken zur
Beschreibung der Kinetik von Photo- und Spinströmen:
|
|
(74) |
bzw. ihrer
c. c. komplex konjugierten photonischen Felder für den positiven
Frequenzbereich:
|
|
(75) |
wobei für
Photo- und Spinströme jetzt die exakte komplexe, nichtlineare Resonanzfunktion
gilt:
|
|
(76) |
Für
hypothetische Photo- und Spinströme, welche durch hohe Harmonische erzeugt
werden können, erhält man unter Berücksichtigung der oben formulierten
Ergebnisse folgende allgemeine Lösungstruktur:
|
|
(77) |
mit der
exakten komplexen, nichtlinearen Resonanzfunktion:
|
|
(78) |
Zur explizit
genaueren Beschreibung der Erzeugung und Dynamik der Photo- und Spinströme
aufgrund der Zweifarbenanregung müssen höhere Näherungen berücksichtigt werden.
Für Näherungen mit einer Genauigkeit bis einschließlich zur 7. nichtlinearen
Ordnung kleiner Größen 
können folgende
Frequenzkorrekturen angegeben werden:
|
|
(79) |
Damit können
die Singularitätskurven mit sehr hoher Genauigkeit berücksichtigt werden. Es
zeigt sich eine verbesserte Kurvenform, welche die Skewness noch besser fittet.
Die nachfolgende Abbildung zeigt die generierte Amplitude der kohärent
erzeugten Photo- und Spinströme analytisch und numerisch. Der Response bei der
2. Harmonischen (w0/2, erzeugt durch die zweite kohärente Quelle mit 
und die Skewness bei
beiden Peaks sind rein nichtlineare Effekte.
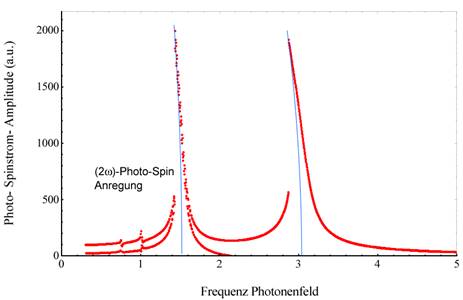
Abbildung 1 zeigt den
charakteristischen Verlauf der nichtlinearen Amplitude der kohärent erzeugten
Photo- und Spinströme als Singularitätslösung (blau) in der Näherung kleiner
Größen 7. nichtlinearer Ordnung und die dissipative Numerische Lösung (rot).
Die neue Modellbildung wird dadurch hervorragend bestätigt.
Verglichen
mit dem stromfreien Response weisen die nichtlinearen Anregungspeaks
niederfrequente und höherfrequente Bereiche auf. Das deutet auf Aufspaltung des
Frequenzbereiches hin. Verglichen mit Versuchsergebnissen aus der Literatur [ ] können
damit die symmetrischen (harmonischen) im Frequenzbereich leicht verschobenen
Mehrfachpeaks mit diesen nichtlinearen Effekten erklärt werden.
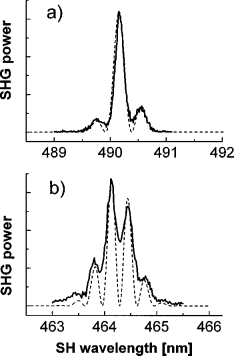
Abbildung 2 zeigt den
charakteristischen Verlauf der 2. Harmonischen an ZnS. Es sind
deutlich weitere Frequenzkomponenten zu erkennen, welche mit den nichtlinearen
Effekten in dieser Arbeit erklärt werden können. aus [H. P. Wagner and M. Kühnelt, W. Langbein and J. M. Hvam, Dispersion
of the second-order nonlinear susceptibility in ZnTe, ZnSe, and ZnS, PHYSICAL
REVIEW B, VOLUME 58, NUMBER 16]
Das
Anregungsmaximum liegt bei diesen "solvatisierten" Elektronen, d. h.
nichtzentrosymmetrisch gebundenen (Oberflächen)elektronen im niederfrequenten
Bereich, was auf Systemstabilisierung durch Energieabsenkung zurückzuführen
ist. Diese entsprechen den angeregten Photo- und Spinstrom an Oberflächen,
welche von "solvatisierten" Elektronen herrühren.
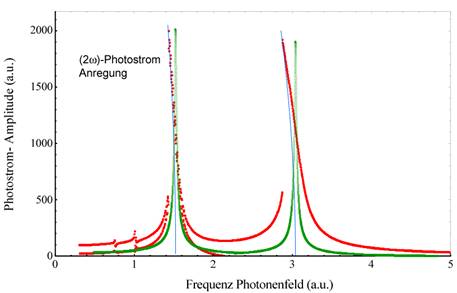
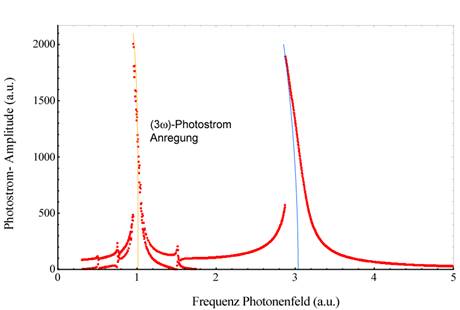
Abbildung 3 zeigt den
oben charakteristischen Verlauf der nichtlinearen Amplitude der kohärent
erzeugten Photostrom im Vergleich zum angeregten linearen Photolumineszenz
Response (grün) und die nichtlinearen Responses der kohärent erzeugten
bichromatischen Anregung mit ω und 3ω in der Näherung kleiner Größen
7. nichtlinearer Ordnung. Es zeigen sich zudem in der Umgebung der höheren
Anregung zusätzliche kleine Amplituden, welche aufgrund höherer
Dipolschwingungen zustande kommen und höhere Harmonischen aus den kohärenten
Anregungsfrequenzen erzeugen.
Zwei
zueinander parallele kohärente Photonenquellen generieren Photoströme. In
Abhängigkeit von der Phasenbeziehung und dem Amplitudenverhältnis der beiden
Wellen ergeben sich für Phasenverschiebungen gemäß 
Photoströme, wobei für
Phasenverschiebungen mit 
maximale
Ladungsströme generiert werden. Für betragsmäßig gleiche optische
Feldamplituden, ist die Ausgangspolarisation elliptisch polarisiert. Für
betragsmäßig unterschiedliche Feldamplituden ergibt sich eine lineare
Ausgangspolarisation deren Richtung vom Amplitudenverhältnis abhängig ist.
Diese maximalen Ladungsströme entsprechen einer harmonischen Anregung, welche
zu keiner Spinstromanregung führt. Das ist der Anregungspunkt, der mit der
Position der angeregten Photolumineszenz ohne Spinströme zusammenfällt. Für
diesen Punkt ergibt sich keine Skewness. Für gekreuzte Lichtfeldpolarisation
mit einer Phasenverschiebung von
, welche in der Optik der Subharmonischen und
Ultrasubharmonischen entsprechen, ergeben sich maximale Spinströme mit
elliptischer Polarisation. Elektronen mit Spin "down" werden aus dem
zentralen spinstromfreien Lumineszenzpunkt heraus nach rechts und Elektronen
mit Spin "up" nach links verschoben. Das bedeutet, dass die Position
der zentralen Photolumineszenzpunktbewegung für Spin "up" nach links
sich wie aufgrund der sich einstellenden negativen Skewness verhalten und für
Spin "down" entsprechend einer positiven Skewness nach rechts
wandern. Für dazwischenliegende Phasendifferenzen von
mit n als Integer, 
, zeigt sich eine Umorientierung der Spinströme durch den
Fluss von Elektronen mit Spin "up" nach rechts und Spin
"down" nach links, ganz analog dem Vorzeichenwechsel der Skewness von
links nach rechts und umgekehrt. Dieser Sachverhalt ist in Abb. (4) gezeigt,
welcher für tieferliegende Bloch Elektronen der Bulkbindungen (mit erhöhter
Löcherkonzentration) gezeigt ist.
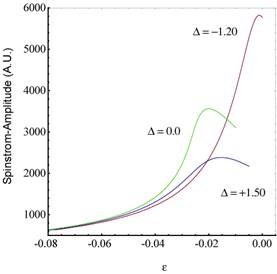
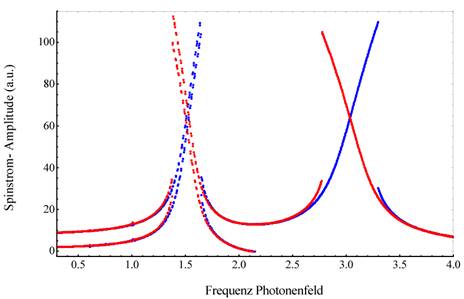
Abbildung 4 zeigt unter Berücksichtigung kohärent
erzeugter Spinströme an Oberflächen (oben) und in den tieferliegenden
Bulkbindungen (unten) den sich ergebenden Skewnesswechsel durch
Phasenverschiebung im nichtlinearen Medium, welcher eine Umpolung der
Spinströme hervorruft.
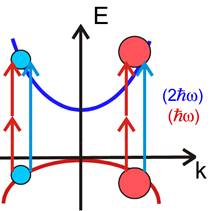
Abbildung 5 zeigt die schematisch die asymmetrische
Anregung für ein Zwei- Band- System. Die Stärke sowie Richtung der Asymmetrie
lassen sich über die Phasenbeziehungen zueinander kohärent kontrollieren.
Aufgrund der
Anregung des Systems mit zwei kohärenten Quellen mit den Zentralfrequenzen
ω und 2ω werden durch Interferenzphänomene asymmetrische Verteilungen
im k- Raum erzeugt. Es kann jetzt angenommen werden, dass durch nichtlineare
Skewnesseffekte diese Asymmetrie verursacht wird. Der zu berücksichtigende
Asymmetriegrad sowie deren Orientierung lassen sich über die Phasenverschiebung
der kohärenten Laserpulse kontrollieren. Der Skewnessbeitrag entspricht dabei
dem Energieunterschied wie er beim Übergang vom Gas über die Flüssigkeit zum
und Festkörper auftritt. Die Skewnessdifferenz entspricht dabei der
aufzubringenden notwendigen Energie zur Umordnung zum Feststoff und zeigt dass
hierfür Energiezufuhr durch Dotierung notwendig ist. Im nichtlinearen Regime
befindet es sich im höher energetischen Zustand. Betrachtet man die Zustände in
solchen Bändern, so ergeben sich im nichtlinearen Regime im Vergleich zu
linearen Systemen signifikante Unterschiede wie in Abb. 6 anschaulich
dargestellt.
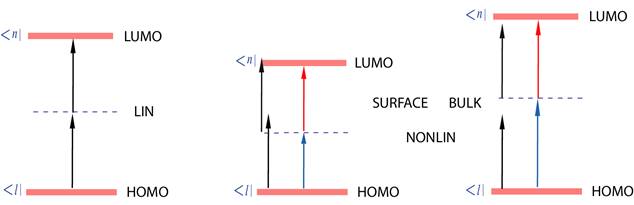
Abbildung 6 zeigt die HOMO und LUMO Grenzzustände /
Grenzorbitale für lineare (links) und nichtlineare Systeme (Mitte und rechts).
In nichtlinearen Systemen ist jeweils abhängig von der Materiesymmetrie eine im
Vergleich zum linearen System niedrigerer HOMO Zustand für
nichtzentrosymmetrische und zentrosymmetrische Materie und höherer HOMO-
Zustand für Bulkmaterialien erhöhter Löcherkonzentration zu erwarten.
Dieser
Energieaspekt wurde bereits gemessen und ist in der Literatur dargestellt.
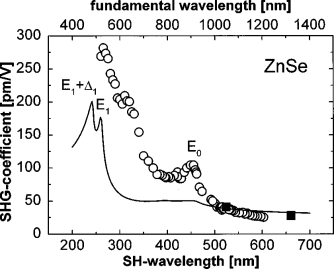
Abbildung 7 zeigt
die experimentell gemessene SHG- Dispersionskurve in ZdSe (Kreise) und die
berechnete Dispersionskurve. Es zeigt sich eine Energieverschiebung in den
höherfrequenten Bereich, aus [H. P. Wagner, M. Kühnelt, W. Langbein, J. M.
Hvam, Dispersion of the second-order
nonlinear susceptibility in ZnTe, ZnSe, and ZnS, PHYSICAL REVIEW B,
VOLUME 58, NUMBER 16]
5. Photonische
Kristalle: Aufgrund von Interferenzphänomenen und Anregung durch
Vielwellenmischen müssen nichtlineare Effekte berücksichtigt werden. Für
photonische Kristallen sind nachfolgende Messergebnisse in der Literatur
bereits dargestellt, welche durch die in dieser Arbeit dargelegten
nichtlinearen Effekte zu erklären sind.
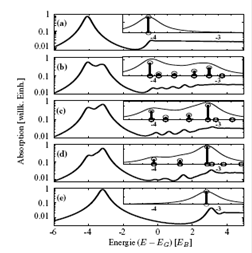
Abb. aus: [Dissertation Bernhard Pasenow, Optische Erzeugung außergewöhnlicher
Ladungsträgerverteilungen
in Halbleiterstrukturen]
Abbildung 8 gemessene Spektralkurven in photonischen
Kristallen mit exzitonischen Resonanzen. Darin ist deutlich die Zerlegung der
Resonanz in gebundene exzitonische Zustände und der exzitonischen
Oszillatorstärke zu erkennen. Für große Breiten (W = 180nm) und für verschwindende
Breiten W=0 der photonischen Kristallstruktur ist ein eindeutige Resonanz zu
beobachten. Für in den Grenzbereichen dazwischenliegende Breiten ergeben sich
energetisch verschobene Doppelpeaks, was eine Verschiebung der Kontinuumskante
zu höheren Energien sowie eine verstärkte exzitonische Bindungsenergie
hindeutet. Diese kommen durch Materiewechselwirkungen zustande, welche
nichtlineare Effekte tragen.
Die
Unterdrückung der Hystereseeffekte in photonischen Kristallen, wie auch in
allen anderen Mikro- und Nanoskaligen Bauteilen, wird von großer Wichtigkeit
werden, um Störungen zu vermeiden welche durch abrupte Änderung in der Dynamik
ihre Ursache haben und um z. B. in photonischen Kristallen einen glatten
Übergang zwischen stabilen Responses in den dielektrischen Schichten
sicherzustellen.
6. Chemisches
Potential: Mit den
Eigenenergien und Eigenfunktionen ergeben sich fermi- Dirac- artige
Gleichgewichtskohärenzen für Elektronen und Löcher gemäß:
|
|
(80) |
Dies
entspricht der nichtlinearen Elektron- und Holon- Photonen Wechselwirkung an
Quantenpunkten (0 Dim. Wechselwirkung). Abb xx.yy zeigt die Nichtlinearen
Singularitäten bis zu kleinen Größen 7. Ordnung. Dabei entsprechen die
Singularitätskurven negativer Skewness der Photonenwechselwirkung mit
solvatisierten Elektronen und Oberflächenbindungselektronen. Für die
photonengetriebenen Wechselwirkung mit den tieferliegenden Bulkbindungen ergibt
sich eine Singularitätsskewnesskurve mit vollständigem Vorzeichenwechsel nur
für Bulkmaterialien mit erhöhter Löcherkonzentration erzeugbar durch Dotierung
mit Elementen der 3. Hauptgruppe (positive Dotierung). Daran ist sehr
anschaulich erkennbar, wie mit den geänderten Eigenfunktionen und Eigenenergien
durch Änderung des chemischen Potentials vom "Fermi"- Gas bzw.
"Fermi"- Flüssigkeit durch einen nichtkontinuierlichen Phasenübergang
2. Ordnung das entropiereiche System in ein entropieärmeres Festkörpersystem
übergeht. Diese nichtlineare chemische Potentialänderung wird aufgrund des
Skewnesswechsels erst ermöglicht.
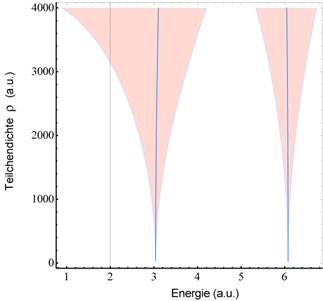
Abbildung 9 zeigt die Singularitäten der Quantenpunkte
nach Multiphotonenwechselwirkung in Abhängigkeit der Materiesymmetrie. Mit
zunehmender Energie werden die stabilen Singularitätsbereiche sehr schnell
schmal. Dies ist ein Indiz dafür, dass Phasenübergänge mit zunehmender Ordnung
immer schwerer zu realisieren sind.
Für die
nichtlineare Dichteverteilung an einem einzelnen Quantenpunkt kann
angeschrieben werden:
|
|
(81) |
mit 
als quantisierte
Energieniveaus, die aus den zusätzlichen Quantisierungen in den Raumrichtungen
resultieren und 
als nichtlineare
Energieverteilung nach Quantenpunkt- Multiphotonenwechselwirkung. Ein
Quantenpunkt kann damit als Deltafunktion formuliert werden welche nach
nichtlinearer Wechselwirkung mit Strahlung mit negativer Skewness behaftet ist,
d.h. es gibt diskrete Energieniveaus welche nun nichtlinear entsprechend der
singulären Skewnesskurven verbogen sind. Einstrahlung höherer Harmonischer
ergibt Deltafunktionen an den natürlichen Resonanzpunkten der Quantenpunkte.
Das sind das die geraden Ordnungen. Auftragen der Elektronendichte als Funktion
der Energie ergeben nichtlineare Singularitätskurven. Für Oberflächenpartikel erfolgt
Energieabsenkung, für tieferliegende Bulkteilchen erfolgt zunächst auch in
etwas abgeschwächterer Ausprägung Systemstabilisierung durch Energieabsenkung.
Unter Einbau von Ladungsunterschüssen (entsprechende Fremdatome,
Verunreinigungen) wird unter nichtlinearen Skewnesswechsel ein Übergang in
einen energetisch höheren Zustand begünstigt, welche dem Umbau in einem
Festkörpervolumen entspricht.
7. Ab initio Nichtgleichgewichtsphänomene;
Das nichtlineare Phasenübergangs- Modell: Bezogen auf die Vielteilchen-
Quantentheorie ist es sinnvoll, Phasenübergänge im Nichtgleichgewicht
detaillierter zu betrachten, d. h. als nichtlineare Übergänge. Dieses Problem
lässt sich mit den entwickelten Methoden lösen. Damit ist es möglich den
Leiter- Nichtleiter- Übergang (Mott- Übergang) in Abhängigkeit der
Kontrollparameter (z. B. Druck) genauer zu beschreiben. Dem nichtlinearem
Phasenübergang 1. Ordnung wird hier gemäß Landau Theorie eine quartäre (freie)
Energie zugrunde gelegt
|
|
(82) |
mit m als
(lokale) Magnetisierung und 
als Temperatur(phase)
und h als magnetisches Feld und für den Fall nichtlinearer Phasenübergänge 2.
Ordnung gemäß Landau Theorie die freie Energie sechster Ordnung, gemäß
|
|
(83) |
Es ergibt
sich nach der entwickelten nichtlinearen Theorie für die quartäre und nur für
die sextäre Landau Energie Hystereseverhalten mit Skew. Der Teilchenresponse
ist in der Mean field Theorie exakter als die Korrelationsfunktion und
wiedergibt die reale Physik. Es kann Hysterese gezeigt werden und beim
kritischen Punkt die Aufspaltung in Nichtleiterbereiche und Leiterbereiche
gemäß der Nichtlinearitäten. Bereiche korrelierter und unkorrelierter
Elektronen entwickeln sich in Abhängigkeit der Temperatur entlang der
Singularitäten. Unter dem Aspekt des Fermionen- Drucks, die besagt, dass der
Energieinhalt der Phase mit der Teilchenzahldichte nichtlinear ansteigt, muss
die kinetische Beschreibung der Phasen der nichtlinearen Energiezunahme im
Vielteilchensystem als Korrektur berücksichtigt werden. Hierzu ist es notwendig
die Differentialgleichungssysteme N- ter Ordnung entsprechend zu modifizieren,
u. a. mit einem zusätzlichen Term zur Beschreibung der Fluktuationen in der
Besetzung der Gitterplätze, entweder als statisches (MFT) oder dynamisches Feld
(DMFT) gemäß:
|
|
(84) |
und
|
|
(85) |
mit 
als konstante Kraft
und 
als Kraft als
stochastische Wahrscheinlichkeitsverteilung. Für die nichtlineare Betrachtung
wird das Verhalten eines Partikels in ein anharmonischen Potentialtopf
untersucht. Laplace- Transformation liefert mit:
|
|
(86) |
Aus der
nichtlinearen Differentialgleichung N- ter Ordnung kann das Partikelverhalten
mittels der Hochenergieentwicklung Greenscher Funktionen beschrieben werden.
Insgesamt ergibt sich für die Greensche- Funktion des Elektronenpartikels im
Festkörper in der Fourier- Domäne:
|
|
(87) |
mit
|
|
(88) |
|
|
(89) |
und 
nichtlineare
Korrekturen gemäß der entwickelten nichtlinearen Theorie in Abhängigkeit ihrer
Symmetrie und Ladungsstruktur, Elektron und Holon. Die allgemeine Lösung der
inhomogenen nichtlinearen Differentialgleichung setzt sich zusammen aus
|
|
(90) |
und liefert
für die nichtlineare Green- Funktion:
|
|
(91) |
mit
|
|
(92) |
und 
für die zu
betrachtende Resonanz. Da die Green- Funktion hier nur von der Zeitdifferenz 
abhängt, kann folgende
modifizierte Formel für das nichtlineare Regime angegeben werden.
|
|
(93) |
mit 
als nichtlineare
Energievariation in Abhängigkeit ihrer jeweiligen Symmetrie und
Ladungsstruktur.
Betrachtet
man hierzu zudem das chemische Potential kann eine Reaktion, Umwandlung oder
Umverteilung freiwillig nur stattfinden, wenn das chemische Potential im
Ausgangszustand größer ist als im Endzustand, d. h. nur für positiven Skew ist
eine Phasenübergang möglich (Bulk, d. h. zum Festkörper). Bei einem
Phasenübergang 1. Ordnung Fermi- Gas zur Fermi- Flüssigkeit gemäß der
zugrundeliegenden Skewness ist nur eine leichte Anhebung des chemischen
Potentials nötig. Beim Phasenübergang zweiter Ordnung, d. h. von der
"Fermi- Flüssigkeit" zum Festkörper erfolgt ein vollständiger
Vorzeichenwechsel. Dieser Phasenübergang erfolgt im Gegensatz zum Übergang 1.
Ordnung nicht kontinuierlich. Dies erklärt den großen Skewnessunterschied von
der "Fermi- Flüssigkeit" zum Festkörper als Phasenübergang zweiter
Ordnung. Damit kann der Übergang zwischen Phasen unterschiedlicher Symmetrie
(z. B. Kristall ↔ Flüssigkeit) und verschiedener kristalliner
Modifikationen (nicht kontinuierlicher Übergang) beschrieben werden.
Kontinuierlicher Übergang, z. B. Gas ↔ Flüssigkeit (lineare Response-
Theorie). Je höher dabei die zu berücksichtigende Teilchenzahl ist, desto mehr
muss in Bandmodellen formuliert werden. Es erfolgt eine Aufspaltung gemäß ihrer
Symmetrie (N.Z.S. und Z.S.) nach oben (Bulk) und unten (Oberfläche). Das
gesamte Band wird aufgebaut aus dem jeweiligen zugrundegelegten nichtlinearen
Potential.
8. Literatur:
[SYR84] Shen, Y.
R. The Principles of Nonlinear Optics; Wiley: New York, 1984.
[BRW03] Boyd, R. W.
Nonlinear Optics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003.
[PFTV92] Press, W.
H., B. P. Flannery, S. A. Teukolsky, und W. T. Vetterling, Numerical Recipes in C, 2nd ed., Press Syndicate of the University of Cambridge, 1992.
[BSMM08] Bronstein,
I. N., K. A. Semendjajew, G. Musiol, H. Mühlig, Taschenbuch der Mathematik,
7., vollständig überarbeitete und ergänzte Auflage, Verlag Harri Deutsch,
Frankfurt am Main, (2008).
[LL07- I] Landau, L. D., E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.I: Mechanik, 14., korrigierte Auflage, Akademie-Verlag, Berlin, (2007).
[LL09- II] Landau, L. D., E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.II: Klassische Feldtheorie, 12. Auflage, Akademie-Verlag, Berlin, (2009).
[LL07- III] Landau, L. D., E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.III: Quantenmechanik, 9. Auflage,
Akademie-Verlag, Berlin, (2007).
[BM65] Bogoljubow, N. N. and J. A. Mitropolski, Asymptotische Methoden in der
Theorie der nichtlinearen Schwingungen, Akademie-Verlag, Berlin (1965).
[Hayashi 64] Hayashi, C., Nonlinear Oscillations in Physical Systems, Princeton
University Press, Princeton, NJ (1964).
[KHK02] Khalil,
Hassan K., Nonlinear Systems, 3rd
International edition, Pearson
Education (2002).