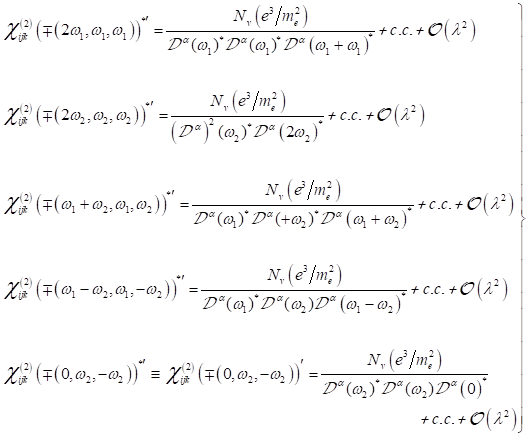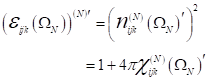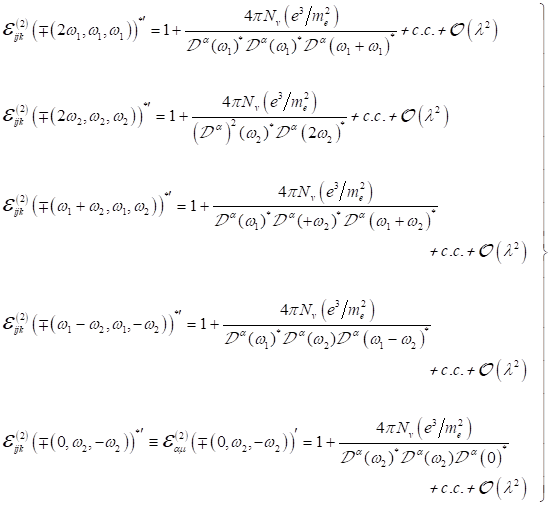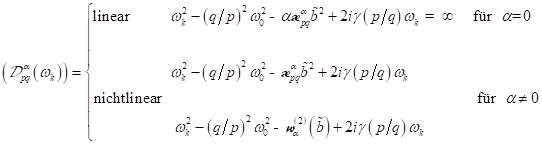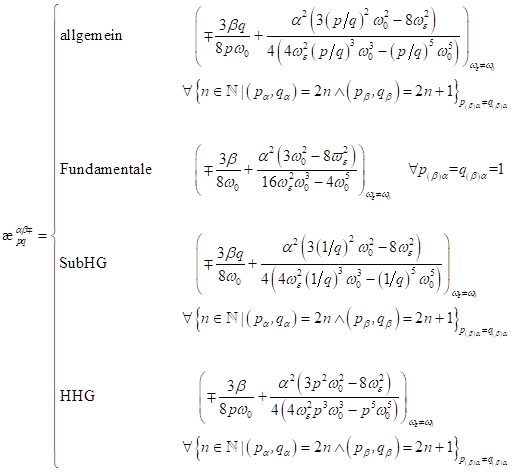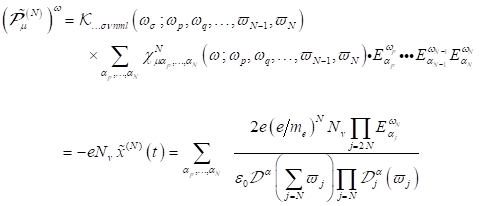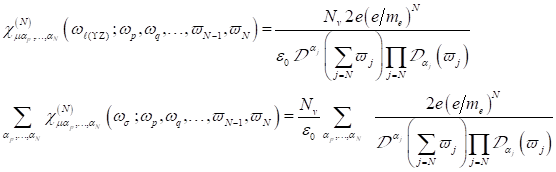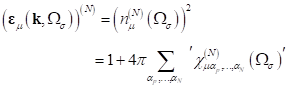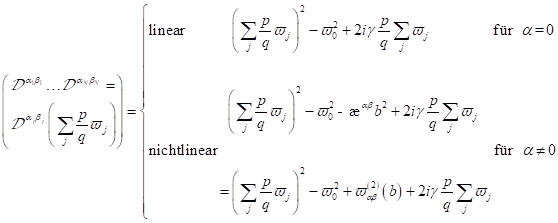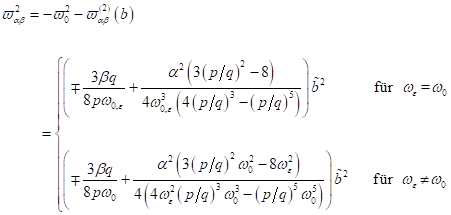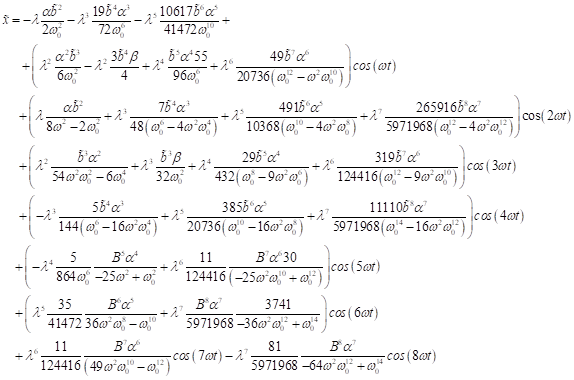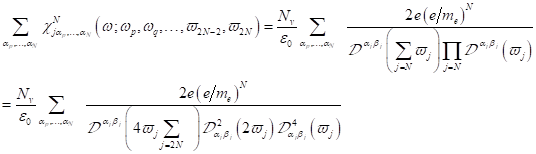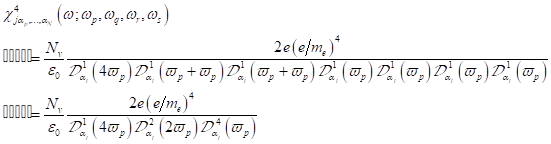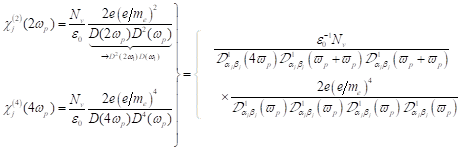Nichtlineare Makroskopische optische
Response Tensoren für 2- Farben Anregung und Elektron- Multiphoton
Wechselwirkung
Peter Krampl*
1. Zusammenfassung: Ein sich ergebener interessanter Aspekt in
dieser Arbeit sei gleich zu Beginn erwähnt. Es zeigte sich, dass die von
nichtzentrosymmetrisch gebundenen Elektronen erzeugten höheren Harmonischen,
Eigenschaften von Negativ- Index- Systemen annehmen können. Durch Kontrolle der Nichtlinearität sind demnach
maßgeschneiderte optische Metamaterialien mit definierten negativen
Brechungsindex möglich. Dies wird interessant im Zusammenhang, dass
Materiewellen mit einem Brechungsindex von exakt minus Eins das perfekte Mikroskop
bilden. Ein geeigneter Satz von neuen charakteristischen optischen
Responsetensoren, welche unter Berücksichtigung der neu hinzugewonnenen
Erkenntnisse nicht mehr lorentzartig sind, wurden für nichtzentrosymmetrische
Medien hergeleitet und dessen Wichtigkeit für die verschiedenen nichtlinearen
orbitalen Responsefunktionen gezeigt und diskutiert. Die nichtlineare resonante
Nennerfunktion kann in Abhängigkeit der Stärke der Nichtlinearität α neu
geschrieben werden, wobei nichtzentrosymmetrische Materie im nichtlinearen
Regime mit negativer SKEWNESS und zentrosymmetrische Materie, sowie der
Übergang Bulk / Oberfläche mit positiver SKEWNESS skaliert und sich die
Harmonischen in Abhängigkeit der eingeführten Parameter p und q klassifizieren
lassen. Die Nichtlinearität in der Nennerfunktion berücksichtigt die
auftretende Skewness und die Destabilisierung zunehmender nichtlinearer
Amplituden, ganz im Gegensatz zur aktuellen Literatur (z. B. Boyd), in der
α lediglich als Proportionalitätsfaktor auftritt, in der die Amplitude
linear und direkt beeinflusst wird und keine Destabilisierung der Amplituden im
nichtlinearen Regime beschrieben wird. Aufgrund der Symmetrie
nichtzentrosymmetrischer Materie sind keine longitudinale Moden
propagationsfähig. Die nichtlineare dielektrische spektrale Antwortfunktion
besitzt für nicht- dissipative Materie Singularitäten bei jeder
Übergangsfrequenz. Die Analyse unter Berücksichtigung dissipativer Effekte
zeigte eine Beseitigung dieser Singularitäten. Man erhält Kurven mit negativer
Skewness. In den identifizierten Bereichen negativer dielektrischer Funktion
existiert ein reeller Brechungsindex kleiner 1. Der Brechungsindex ist dort
imaginär, was normalerweise charakteristisch für Oberflächenplasmonen ist. In
diesem Bereich ist es prinzipiell möglich durch Einstellen geeigneter
Nichtlinearität optische Metamaterialien zu erzeugen. Im linearen Fall besitzt
die Spektralfunktion eine Nullstelle, sodass hierfür auch longitudinale Moden
propagieren können. Variation der Nichtlinearität bewirkt abhängig vom
Vorzeichen einen sehr großen positiven bzw. negativen Skew und zeigt
Frequenzkonversion. Die nichtlineare
elektrische Suszeptibilität für Oberflächenpartikel durch Verschiebung in den
niederfrequenteren Bereich begünstigt. Für gewöhnlichen Bulk etwas schwächer
ausgeprägt ebenfalls, ganz im Gegensatz zu positiv dotierten Bulk der
höherfrequenter zur Resonanz besser zu polarisieren und anzuregen ist. Somit
ist die nichtlineare elektrische Suszeptibilität, abhängig von der Materialsymmetrie
frequenzabhängig. Somit wirken Oberflächen im leicht unterhalb der
Anregungsfrequenz optisch dichter und realer Materialbulk oberhalb ihrer
Anregungsfrequenz dichter. Störende Skew- Effekte in Bauteilen zum Beispiel
lassen sich demnach durch Materialien variierender Brechungsindices beseitigen.
Der nichtlineare Brechungsindex kann in der Form ![]() angegeben werden. Damit variiert der
Brechungsindex gemäß der Singularitäten bzw. mit zunehmender Unschärfe (Breite
der Kurve, erhöhter Variationsbereich des Brechungsindexes) in dissipativer
Umgebung. Der Index kann mit der Intensität kontrolliert werden.
angegeben werden. Damit variiert der
Brechungsindex gemäß der Singularitäten bzw. mit zunehmender Unschärfe (Breite
der Kurve, erhöhter Variationsbereich des Brechungsindexes) in dissipativer
Umgebung. Der Index kann mit der Intensität kontrolliert werden.
2. Nichtlineare Suszeptibilität
und Brechungsindex: In dieser
Arbeit wird der nichtlineare Skewness- Effekt im Kontext der nichtlinearen
makroskopischen Response- Tensoren in dissipativer Umgebung diskutiert. Wie in
den vorhergehenden Arbeiten [PKM] gezeigt, lassen sich
für die die makroskopischen optischen Response Tensoren im nichtlinearen
Regime exakt nichtlineare analytische Ausdrücke für die optischen Response
Tensoren angeben. Die nichtlineare orbitale Suszeptibilität in der ersten
nichtlinearen Näherung kleiner Größen ![]() zur Beschreibung der
Wechselwirkung von bichromatischen Photonenfeldern mit nichtzentrosymmetrischer
Materie ergibt Ausdrücke, welche für komplex konjugierte Felder in dissipativer
Umgebung behobene Singularitäten bei den Resonanzen mit den Frequenzen -2ω1,
-2ω2, -(ω1+ω2), -(ω1−ω2)
besitzt, welche einen amplitudenabhängigen negativen Skew aufweisen. Für NZS
& ZS- Materie zeigt sich ein negativer Skew, für die Schnittstelle
Oberfläche / Bulk und ladungsunterschüssigen Bulk stellt sich ein positiver
Skew ein.
zur Beschreibung der
Wechselwirkung von bichromatischen Photonenfeldern mit nichtzentrosymmetrischer
Materie ergibt Ausdrücke, welche für komplex konjugierte Felder in dissipativer
Umgebung behobene Singularitäten bei den Resonanzen mit den Frequenzen -2ω1,
-2ω2, -(ω1+ω2), -(ω1−ω2)
besitzt, welche einen amplitudenabhängigen negativen Skew aufweisen. Für NZS
& ZS- Materie zeigt sich ein negativer Skew, für die Schnittstelle
Oberfläche / Bulk und ladungsunterschüssigen Bulk stellt sich ein positiver
Skew ein.
|
|
(1) |
Die
nichtlineare Suszeptibilität in ![]() setzt sich aus der
Summe all dieser Komponenten zusammen. Mithilfe der Dispersionstheorie lässt
sich auf den exakten molekularen Dielektrizitätstensor beliebiger Ordnung
schließen und somit der nichtlineare Brechungsindex exakt analytisch bestimmen.
Für homogene, isotrope Materie kann man anschreiben:
setzt sich aus der
Summe all dieser Komponenten zusammen. Mithilfe der Dispersionstheorie lässt
sich auf den exakten molekularen Dielektrizitätstensor beliebiger Ordnung
schließen und somit der nichtlineare Brechungsindex exakt analytisch bestimmen.
Für homogene, isotrope Materie kann man anschreiben:
|
|
(2) |
wobei ![]() die optischen
Pumpfrequenzen darstellen. Die nichtlinearen Spektraleigenschaften im Fourier-
Raum können damit zusammenfassend für bichromatische c. c. Photonenfelder und
deren komplex konjugierten Felder wie folgt angegeben werden:
die optischen
Pumpfrequenzen darstellen. Die nichtlinearen Spektraleigenschaften im Fourier-
Raum können damit zusammenfassend für bichromatische c. c. Photonenfelder und
deren komplex konjugierten Felder wie folgt angegeben werden:
|
|
(3) |
Dabei ist zu
beachten, dass die Nichtlinearität α in der komplexen nichtlinearen
Resonanzfunktion nur noch im Nenner auftritt. Definiert auf die tatsächlich im
Spektrum auftretenden reziproken Frequenzen lässt sich anschreiben:
|
|
(4) |
mit den
Anharmonizitätskoeffizienten, ![]() , welche allgemein die Skewness für Harmonische und
Subharmonische beliebiger Ordnung mit einer Genauigkeit
, welche allgemein die Skewness für Harmonische und
Subharmonische beliebiger Ordnung mit einer Genauigkeit ![]() berücksichtigt.
berücksichtigt.
|
|
(5) |
Damit kann
mittels der Nichtlinearität die Skewenss exakt berücksichtigt werden. Weiters
sagen die Ausdrücke eine destabilisierende Wirkung auf die Amplitude für hohe
Felder vorher. In der aktuellen Literatur, wird die Nichtlinearität α als
Proportionalitätsfaktor berücksichtigt. Demzufolge würde der Betrag der
Amplitude mit zunehmender Nichtlinearität ebenfalls zunehmen und dass auch noch
stabil. Weiters bewirkt in der bisherigen Modellbildung ein Vorzeichenwechsel
der Nichtlinearität eine vollständige Amplitudenumkehr, was bedeuten würde,
dass aus Emmission, nach Durchlaufen der Nichtlinearität eines vollständigen
Vorzeichens, Absorption wird, was physikalisch unsinnig ist. In der
verbesserten Modellbildung bewirkt ein Vorzeichenwechsel in der Nichtlinearität
einen Skewnesswechsel, was Sinn macht.
Der nichtlineare
Brechungsindex kann in der Form ![]() entwickelt werden, wobei
entwickelt werden, wobei ![]() der Index ist, welcher
generiert wird durch schwache Felder (an der Resonanzfrequenz und deren kleinen
Umgebung) und mit
der Index ist, welcher
generiert wird durch schwache Felder (an der Resonanzfrequenz und deren kleinen
Umgebung) und mit ![]() als eine neue optische
Indexvariation gemäß der ermittelten Singularitäten, in welcher der Index
zunimmt bzw. abnimmt, jeweils in Abhängigkeit des zugrundeliegenden Skews.
Damit bleibt der nichtlineare Index Intensitätsabhängig ist aber im Gegensatz
zur bisherigen Literatur keine einfache Konstante mehr, sondern variiert mit
der Intensität im nichtlinearen Regime und kann damit kontrolliert werden. Somit nimmt an Oberflächen der Brechungsindex
im nichtlinearen Regime ab, der ladungsüberschüssige Bulk etwas schwächer ab
und der "reale" Bulk im Ladungsunterschuss entsprechend der
Nichtlinearität zu.
als eine neue optische
Indexvariation gemäß der ermittelten Singularitäten, in welcher der Index
zunimmt bzw. abnimmt, jeweils in Abhängigkeit des zugrundeliegenden Skews.
Damit bleibt der nichtlineare Index Intensitätsabhängig ist aber im Gegensatz
zur bisherigen Literatur keine einfache Konstante mehr, sondern variiert mit
der Intensität im nichtlinearen Regime und kann damit kontrolliert werden. Somit nimmt an Oberflächen der Brechungsindex
im nichtlinearen Regime ab, der ladungsüberschüssige Bulk etwas schwächer ab
und der "reale" Bulk im Ladungsunterschuss entsprechend der
Nichtlinearität zu.
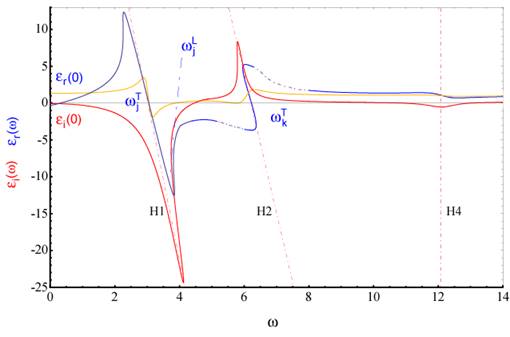
Die nachfolgenden
Abbildungen zeigen den berechneten nichtlinearen dielektrischen Spektral-
Response ε(ω) für die Licht- Materie Wechselwirkung im extrem
nichtlinearen Regime. Die nichtlineare dielektrische spektrale Antwortfunktion
besitzt für nicht- dissipative Materie Singularitäten bei jeder
Übergangsfrequenz ![]() . Der erste Peak mit negativer Imaginarität zeigt Absorption und
der zweite Peak zeigt ein dazu inverses Verhalten mit positiver Imaginarität.
Der Realteil der dielektrischen Funktion identifiziert an den Flanken der
ersten Übergangsfrequenz normale Dispersion und anormale Dispersion in einem
schmalen Band um die Übergangsfrequenz
. Der erste Peak mit negativer Imaginarität zeigt Absorption und
der zweite Peak zeigt ein dazu inverses Verhalten mit positiver Imaginarität.
Der Realteil der dielektrischen Funktion identifiziert an den Flanken der
ersten Übergangsfrequenz normale Dispersion und anormale Dispersion in einem
schmalen Band um die Übergangsfrequenz ![]() und in der Umgebung
der zweiten Übergangsfrequenz
und in der Umgebung
der zweiten Übergangsfrequenz ![]() dazu ein Gebiet
inverser Dispersion. Die Dispersion hat hier das umgekehrte Vorzeichen wie bei
einer gewöhnlichen absorptiven Resonanz, d. h. sie ist „normal“ am Übergang und
anormal an den Flanken. Dies deutet auf eine Dunkelresonanz hin. Insbesondere
ist in diesem schmalen Band größter Imaginärwerte für normale Dispersion ein
Wendepunkt und Vorzeichenwechsel des Index- Systems nachzuweisen. Die starke
Änderung des Brechungsindexes wird induziert durch die Dunkelresonanz, welche
in einem extrem schmalen Bereich sehr stark ausgeprägt ist. Die
Relaxationsfrequenzen liegen jeweils bei den Harmonischen gerader, d. h. 2N- ter
Ordnung. Im Frequenzbereich
dazu ein Gebiet
inverser Dispersion. Die Dispersion hat hier das umgekehrte Vorzeichen wie bei
einer gewöhnlichen absorptiven Resonanz, d. h. sie ist „normal“ am Übergang und
anormal an den Flanken. Dies deutet auf eine Dunkelresonanz hin. Insbesondere
ist in diesem schmalen Band größter Imaginärwerte für normale Dispersion ein
Wendepunkt und Vorzeichenwechsel des Index- Systems nachzuweisen. Die starke
Änderung des Brechungsindexes wird induziert durch die Dunkelresonanz, welche
in einem extrem schmalen Bereich sehr stark ausgeprägt ist. Die
Relaxationsfrequenzen liegen jeweils bei den Harmonischen gerader, d. h. 2N- ter
Ordnung. Im Frequenzbereich ![]() der transversalen
Übergangsfrequenzen, d. h. zwischen der 2. und 4. Harmonischen, ist die
dielektrische Funktion negativ, und somit ein reeller Brechungsindices kleiner
1,
der transversalen
Übergangsfrequenzen, d. h. zwischen der 2. und 4. Harmonischen, ist die
dielektrische Funktion negativ, und somit ein reeller Brechungsindices kleiner
1, ![]() möglich. Der
Brechungsindex
möglich. Der
Brechungsindex ![]() ist imaginär d. h. n =
0 und
ist imaginär d. h. n =
0 und ![]() , was normalerweise charakteristisch für Oberflächenplasmonen
und Festkörperplasmonen ist. In diesem Bereich ist es prinzipiell möglich durch
Einstellen geeigneter Nichtlinearität optische Metamaterialien zu erzeugen.
Außerhalb des Frequenzbereichs
, was normalerweise charakteristisch für Oberflächenplasmonen
und Festkörperplasmonen ist. In diesem Bereich ist es prinzipiell möglich durch
Einstellen geeigneter Nichtlinearität optische Metamaterialien zu erzeugen.
Außerhalb des Frequenzbereichs ![]() ist
ist ![]() und
und ![]() , der Reflektionskoeffizient ist also kleiner als Eins.
, der Reflektionskoeffizient ist also kleiner als Eins.
|
|
|
|
|
|
|
|
|
|
|
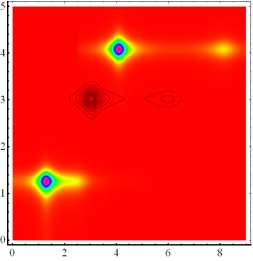
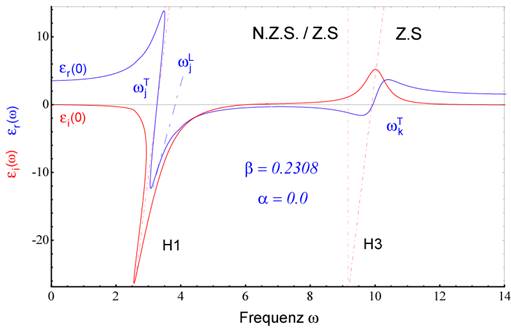
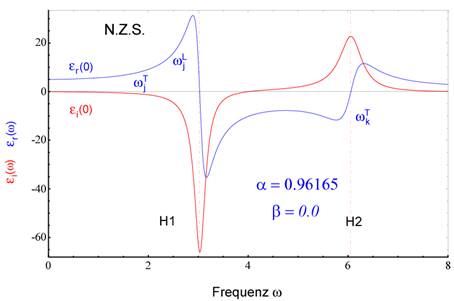
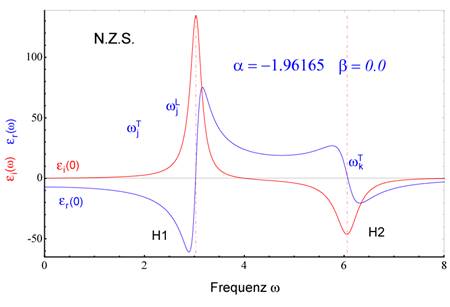
Abbildung 1 (oben)
Phasen- und Amplitudendichten als Funktion der Frequenz im
nichtzentrosymmetrischen Modell für Silizium und HeNe- Laser Puls im extrem
nichtlinearen Regime mit einer optischen Feldamplitude von E = 1.0x10^12 V/cm,
B=0.7*10^5. Die Phasen und Amplituden werden für sehr hohe Harmonische extrem
klein. Deshalb wurde die Phasen- und Amplitudenverteilung um die 4. Harmonische
aus Darstellungsgründen höher gewichtet. Aufgrund der Symmetrie sind keine
longitudinale Moden propagationsfähig. Das nichtlineare System ist damit vom
linearen Fall isoliert. Die lineare Phasen- und Intensitätsverteilung sind
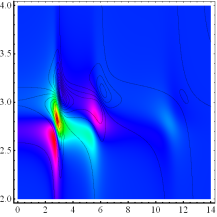
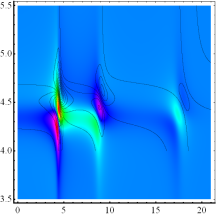
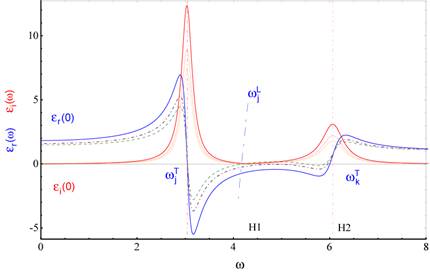
entsprechend als Contourlinien berücksichtigt. (Mitte) Exemplarische Darstellung der berechneten Phasen (Realteil)
und Amplitude (Imaginärteil) des nichtlinearen dielektrischen Spektral-
Responses ε(ω) für 6.5*10^10 Partikel, Nichtlinearität, α =
4.6165 in nichtzentrosymmetrischen, dissipativen Medien mit γ = 0.13494.
Die nichtlineare dielektrische spektrale Antwortfunktion besitzt für nicht-
dissipative Materie Singularitäten bei jeder Übergangsfrequenz ![]() . Die gestrichelten Geraden zeigen die Orte der
Singularitäten. Die Analyse unter Berücksichtigung dissipativer Effekte
beseitigt diese Singularitäten. Wir erhalten Kurven mit negativer Skewness.
Zusätzlich gelb eingezeichnet ist der reelle lineare Fall. Die lineare
Spektralfunktion hat bei dem extrapolierten Wert wjl eine Nullstelle, sodass
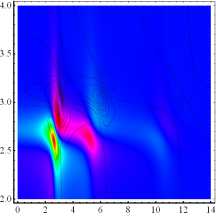
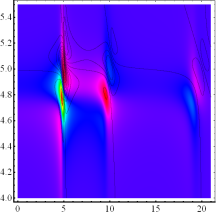
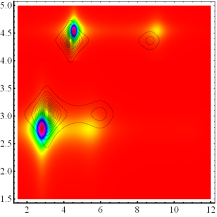
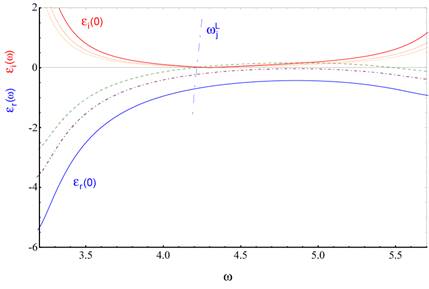
hierfür auch longitudinale Moden propagieren können. (Unten) Intensitätsverteilung Si- Kristall mit He- Ne- Puls in hochdisspativer
Umgebung (γ =0.23) für verschiedene Nichtlinearitäten α im extrem
nichtlinearen Regime simuliert durch kleine Amplituden mit sehr großen
Nichtlinearitätskoeffizienten
. Die gestrichelten Geraden zeigen die Orte der
Singularitäten. Die Analyse unter Berücksichtigung dissipativer Effekte
beseitigt diese Singularitäten. Wir erhalten Kurven mit negativer Skewness.
Zusätzlich gelb eingezeichnet ist der reelle lineare Fall. Die lineare
Spektralfunktion hat bei dem extrapolierten Wert wjl eine Nullstelle, sodass
hierfür auch longitudinale Moden propagieren können. (Unten) Intensitätsverteilung Si- Kristall mit He- Ne- Puls in hochdisspativer
Umgebung (γ =0.23) für verschiedene Nichtlinearitäten α im extrem
nichtlinearen Regime simuliert durch kleine Amplituden mit sehr großen
Nichtlinearitätskoeffizienten ![]() . Die sehr starke Variation der Nichtlinearität mit
. Die sehr starke Variation der Nichtlinearität mit ![]() bewirkt
abhängig vom Vorzeichen einen sehr großen positiven bzw. negativen Skew (links
unten und rechts oben) und zeigt Frequenzkonversion. Aufgrund der
Materiesymmetrie werden nur geradzahlige Harmonische generiert. Die
hochsdissipative Umgebung bewirkt ein
Verschmieren der Intensitäten für
positive Nichtlinearitäten (l. u.). Die
Nichtlinearität durchläuft ein vollständiges Vorzeichen und macht den Einfluß
der Skewness deutlich sichtbar. In der Nähe der Nullstelle der Nennerfunktion
verstärkt sich die Intensitätsdeformation (links unten). Für ein umgekehrtes
Vorzeichen der Nichtlinearität verschiebt sich das Maximum in die
entgegengesetzte Richtung (rechts oben). Zum Vergleich ist der schwach
nichtlineare Fall mit Realwerten für Kristalle
bewirkt
abhängig vom Vorzeichen einen sehr großen positiven bzw. negativen Skew (links
unten und rechts oben) und zeigt Frequenzkonversion. Aufgrund der
Materiesymmetrie werden nur geradzahlige Harmonische generiert. Die
hochsdissipative Umgebung bewirkt ein
Verschmieren der Intensitäten für
positive Nichtlinearitäten (l. u.). Die
Nichtlinearität durchläuft ein vollständiges Vorzeichen und macht den Einfluß
der Skewness deutlich sichtbar. In der Nähe der Nullstelle der Nennerfunktion
verstärkt sich die Intensitätsdeformation (links unten). Für ein umgekehrtes
Vorzeichen der Nichtlinearität verschiebt sich das Maximum in die
entgegengesetzte Richtung (rechts oben). Zum Vergleich ist der schwach
nichtlineare Fall mit Realwerten für Kristalle ![]() als Contour-
Linien Plot mit eingezeichnet.
als Contour-
Linien Plot mit eingezeichnet.
Der sich
anschließende Bereich des Resonanzdurchgangs der 4. Harmonischen zeigt wieder
normale Dispersion mit positiven Index und kleiner positiver Imaginarität. Für
noch größere Frequenzen stellt sich ein konstanter positiver Index ein. Für
höhere Harmonische ist eine Plateauphase des dielektrischen Responses zu
beobachten. Das deutet auf einen Polarisationseffekt hin, dessen Wirkung zu
Harmonischen höherer Ordnungen nachlässt. Dieselben Effekte sind für hohe
Nichtlinearitäten ebenfalls zu beobachten. Der Relaxationspeak (reelle
Dielektr. Resp.) bei höheren Harmonischen ist wesentlich kleiner und zu
geringeren Frequenzen, für positive Brechungsindices (=reelle Indices),
verschoben und entsprechend zu höheren Frequenzen für negative Brechungsindices
(=imaginärer Index) verschoben. Wie aus Abb. (1, Mitte) weiters ersichtlich
ist, besitzt die reelle lineare dielektrische Funktion bei ![]() eine Nullstelle und daher
können, ganz im Gegensatz zum nichtlinearen Fall, zusätzlich zu transversalen
Moden auch longitudinale Moden durch nichzentrosymmetrische Materie mit der
Frequenz
eine Nullstelle und daher
können, ganz im Gegensatz zum nichtlinearen Fall, zusätzlich zu transversalen
Moden auch longitudinale Moden durch nichzentrosymmetrische Materie mit der
Frequenz ![]() propagieren.
Bemerkenswert ist hierbei, dass für hohe Nichtlinearitäten der reelle
dielektrische Response keine Nullstelle
bei
propagieren.
Bemerkenswert ist hierbei, dass für hohe Nichtlinearitäten der reelle
dielektrische Response keine Nullstelle
bei ![]() aufweist und sich
somit für den nichtlinearen Fall in nichtzentrosymmetrischer Materie keine
longitudinalen Moden ausbreiten. Demnach ist diese spezielle Anregungsform, die
an der Oberfläche mit der Frequenz wl propagieren kann, nicht
möglich. Die numerische Analyse zeigt zudem, dass in hochdissipativer und
niedrigsdissipativer Materie, sowie im extrem nichtlinearen Regime, in keiner
auch noch so abgeschwächten Ausprägung, longitudinale Modenpropagation möglich
sind. Das nichtlineare System kann nicht in ein lineares System dissipiert
werden und demnach sind nur transversale Moden möglich. Dies zeigt sehr
anschaulich, dass an Oberflächen oder allgemein an nichtzentrosymmetrischer
Materie Mikro- und Nanostrukturen für Metamaterialien erzeugt werden können.
Diese werden über die Einstellung der Nichtlinearität explizit definiert und
maßgeschneiderte Metamaterialien mit definierten negativen Brechungsindex sind
möglich. Negativ- Index- Systeme von exakt -1 sind das perfekte Mikroskop. Die
Negativbrechung ist aber besser an Metalloberflächen handhabbar, da hier
Oberflächenplasmonen entstehen, deren Ladungsträger- Dichteschwankungen sich
mit der Plasmafrequenz
aufweist und sich
somit für den nichtlinearen Fall in nichtzentrosymmetrischer Materie keine
longitudinalen Moden ausbreiten. Demnach ist diese spezielle Anregungsform, die
an der Oberfläche mit der Frequenz wl propagieren kann, nicht
möglich. Die numerische Analyse zeigt zudem, dass in hochdissipativer und
niedrigsdissipativer Materie, sowie im extrem nichtlinearen Regime, in keiner
auch noch so abgeschwächten Ausprägung, longitudinale Modenpropagation möglich
sind. Das nichtlineare System kann nicht in ein lineares System dissipiert
werden und demnach sind nur transversale Moden möglich. Dies zeigt sehr
anschaulich, dass an Oberflächen oder allgemein an nichtzentrosymmetrischer
Materie Mikro- und Nanostrukturen für Metamaterialien erzeugt werden können.
Diese werden über die Einstellung der Nichtlinearität explizit definiert und
maßgeschneiderte Metamaterialien mit definierten negativen Brechungsindex sind
möglich. Negativ- Index- Systeme von exakt -1 sind das perfekte Mikroskop. Die
Negativbrechung ist aber besser an Metalloberflächen handhabbar, da hier
Oberflächenplasmonen entstehen, deren Ladungsträger- Dichteschwankungen sich
mit der Plasmafrequenz![]() als Wellen im
Material fortpflanzen. Sie lassen sich in Wellenleitern durch die Schichtdicke
ausgewählter Metalle und Isolatoren sehr präzise steuern. So ist es
beispielsweise mit einer Plasmonen- Erregung mit blau- grünem Licht in einem
Sandwich aus Wellenleitern gelungen, Elektronenschwingungen zu erzeugen, die
Licht abstrahlen und zwar in einem Winkel, der negativer Lichtbrechung
entspricht[1].
als Wellen im
Material fortpflanzen. Sie lassen sich in Wellenleitern durch die Schichtdicke
ausgewählter Metalle und Isolatoren sehr präzise steuern. So ist es
beispielsweise mit einer Plasmonen- Erregung mit blau- grünem Licht in einem
Sandwich aus Wellenleitern gelungen, Elektronenschwingungen zu erzeugen, die
Licht abstrahlen und zwar in einem Winkel, der negativer Lichtbrechung
entspricht[1].
3. Bulk und Übergang Oberfläche / Bulk: An der Schnittstelle Oberfläche /
Bulk (Konturlinien oben) besitzt das System bereits negative Nichtlinearität,
was anschaulich zeigt, dass der Skew des Bulks prägender auf das Gesamtsystem
wirkt, als die Skewness der Oberfläche. Die nachfolgenden Abbildungen (6.1- 6.5) zeigen zum Vergleich die berechneten
Phasen- und Amplitudendichten und den nichtlinearen dielektrischen Spektral-
Response ε(ω), sowie die Intensitätsdichten für zentrosymmetrische
Materie und deren Oberfläche / Bulk Übergang zur nichtzentrosymmetrischen
Materie im extrem nichtlinearen Regime. Die nichtlineare dielektrische
spektrale Antwortfunktion für zentrosymmetrische Materie und deren Oberfläche /
Bulk Übergang besitzt hierbei nahezu dieselben Eigenschaften wie für
nichtzentrosymmetrische Materie. Unterschiede sind zu finden in der
Skewnesskompensation mit Skewnesswechsel, die Generation ausschließlich
ungeradzahliger hoher Harmonischer und vor allem die beinahe Nullstelle, die
eine markanten Eigenschaftsunterschied zur nichtzentrosymmetrischen Materie
bedeutet. Im approximativen Grenzfall, kann dieses als Nullstelle gewertet
werden, was bedeutet, dass neben transversalen Moden zusätzlich auch
longitudinale Modenpropagation im Festkörperbulk beobachtet werden können.
|
|
|
Abbildung 2 (oben)
Phasen- und Amplitudendichten als Funktion der Frequenz im zentrosymmetrischen
Modell (Bulk) und deren Übergang Oberfläche / Bulk für Silizium und HeNe- Laser
Puls im extrem nichtlinearen Regime mit einer optischen Feldamplitude von E =
1.0x10^12 V/cm, B=0.5*10^5. Die Phasen- und Intensitätsverteilung für den Bulk
sind zum direkten Vergleich entsprechend als Contourlinien mit eingezeichnet.
Es ist offensichtlich zu erkennen, dass die Skewness im extrem nichtlinearen
Regime die Lage der Resonanzstellen deutlich verschiebt, (wenn hohe Amplituden
B=50 000 zugelassen werden). Im Skew könnte die Ursache für die Generation der
ungeraden Harmonischen liegen, welche die 3. Harmonische hier bei 3*3=9
bewirkt;. Aber auch die Fundamentale wird stark nach höheren Frequenzen
verschoben.
|
|
|
|
|
Abbildung 3 (oben)
Intensitätsverteilung des mit He- Ne- Puls angeregten Si- Kristalls in
hochdisspativer Umgebung (γ =0.32) für zentrosymmetrische (Bulk, oben) und
nichtzentrosymmetrische Medien (Oberfläche, unten) und deren Schnittselle
(Konturlinien oben). Die Oberfläche besitzt negative Skewness, der Bulk wirkt
entgegengesetzt mit positiver Skewness (bei Ladungsunterschuss). Der
Nichtlinearitätskoeffizient α durchläuft beim Übergang von
nichtzentrosymmetrischer Materie zu zentrosymmetrischer Materie dabei ein
vollständiges Vorzeichen und macht den Einfluss der Skewness deutlich sichtbar.
Dabei werden für zentrosymmetrische Materie die Intensitäten nach höheren Frequenzen
verschoben, ganz im Gegensatz zur nichtzentrosymmetrischen Materie deren
Intensitäten gemäß positiver Skewness nach links verschoben werden. (unten): Nichtlineare dielektrischen
Spektral- Response ε(ω) zentrosymmetrischer Materie im Rahmen der
erweiterten nichtlinearen Theorie. Der Realteil besitzt in approximativer
Näherung eine Nullstelle zwischen den beiden Harmonischen. Damit sind im Bulk
auch neben transversalen Phonenmoden auch longitudinale Phononenmoden
propagierbar.
4. Spektraleigenschaften im Rahmen der linearen Approximationstheorie: Zum
Vergleich ist der" lineare, harmonische" Fall mit eingezeichnet
(Kontur- Linien Plot unten α=β= 0.0). Im Skew könnte die Ursache für
die Frequenzkonversion liegen. Im Bulk werden ungerade Harmonische generiert,
hier die 3. Harmonische, welche bei der dreifachen Frequenz der Fundamentalen
(ω=9+ kleine Abweichung durch Skew) identifiziert werden kann. Oberflächen
generieren gerade Harmonische, welche bei ω=6 unter Berücksichtigung
positiver Skewness etwas links davon liegt. Der "lineare" Fall
(α=β=0) ergibt erwartungsgemäß exakt an den Resonanzstellen die
Intensitäten aus, welche den Sachverhalt nach der aktuellen Modellbildung, wie
z. B. nach [Boyd], wiederspiegelt.
|
|
|
|
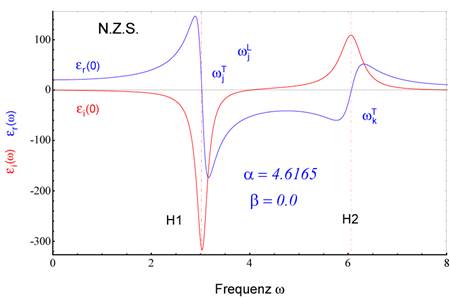
Abbildung 4 zeigt den nichtlinearen dielektrischen
Spektral- Response ε(ω) nichtzentrosymmetrischer
Materie im Rahmen der linearen Approximationstheorie der aktuellen Literatur
[Boyd].
Variationen der nichtlinearen Parameter lassen
folgende relevante Rückschlüsse zu und ist in der nachfolgenden Abbildungsreihe
anschaulich illustriert. Der Realteil ist für kleine positive Nichtlinearität
(0 < α,β << 1) unsymmetrisch bezüglich der Frequenzachse und
zwar für positive Amplituden (Amplitude im positiven größer als im Negativen).
Für Nichtlinearitäten größer 1 (α > 1) verschiebt sich die Asymmetrie
zugunsten negativer Realwerte. Vorzeichenänderung von α,β bewirkt
eine Achsen- Spiegelung der Kurve an der Frequenzachse. Im Imaginärteil wirkt
die Nichtlinearität direkt auf die Amplitude und verstärkt diese. Keine
weiteren Asymmetrien beobachtbar. Vorzeichenwechsel der Nichtlinearität
bewirkt, wie schon beim Realteil zu beobachten war, eine Spiegelung der Kurve
an der Frequenzachse. Nachfolgende Abbildungen zeigen dies anschaulich.
|
|
|
|
|
|
Abbildung 5 zeigt den nichtlinearen dielektrischen
Spektral- Response ε(ω) nichtzentrosymmetrischer
Materie im Rahmen der linearen Approximationstheorie der aktuellen Literatur
[Boyd]. Dabei gehen die beiden Nichtlinearitäten als Proportionalitätsfaktor in auf der
linearen Theorie basierenden Gleichungen ein (oben und Mitte). Inversion der Nichtlinearitäten bewirkt für die
nichtlineare dielektrischen Funktion Achsenspiegelung bezüglich der
Frequenzachse (unten). Das Verhalten
der nichtlinearen Spektralfunktion steht im krassen Gegensatz zur genaueren
entwickelten nichtlinearen Theorie der Licht- Materie Wechselwirkung.
5. Multiphotonenwechselwirkung
N- ter Ordnung: allgemeine analytische ab initio Ausdrücke der neuen
Modellbildung: Mit den
neu gewonnenen Erkenntnissen können wir die nichtlineare Optik durch folgenden
extrem kompakten Satz von nichtlinearen, makroskopischen optischen Response
Tensoren ![]() ,
, ![]()
![]() und
und ![]() N- ter gerader Ordnung
exakt analytisch darstellen.
N- ter gerader Ordnung
exakt analytisch darstellen.
|
|
(6) |
mit
|
|
(7) |
und
|
|
(8) |
mit ![]() als Summe der
eingestrahlten Frequenzen und
als Summe der
eingestrahlten Frequenzen und ![]() , welche die räumlichen Richtungen indizieren. Die zugrunde
gelegte intrinsische Permutationssymmetrie impliziert Invarianz unter allen N!
Permutationen der Paare
, welche die räumlichen Richtungen indizieren. Die zugrunde
gelegte intrinsische Permutationssymmetrie impliziert Invarianz unter allen N!
Permutationen der Paare ![]()
![]() , …,
, …, ![]() . Dabei charakterisieren die Materialeigenschaften mit
. Dabei charakterisieren die Materialeigenschaften mit ![]() die Plasmafrequenz.
Die zugrundegelegte komplexe „nichtlineare“ Resonanzfunktion für SFG in NZS-
Materie genügt den Gleichungen:
die Plasmafrequenz.
Die zugrundegelegte komplexe „nichtlineare“ Resonanzfunktion für SFG in NZS-
Materie genügt den Gleichungen:
|
|
(9) |
wobei
nichtzentrosymmetrische Materie im nichtlinearen Regime mit negativer SKEWNESS
und zentrosymmetrische Materie, sowie der Übergang Bulk / Oberfläche mit
positiver SKEWNESS skaliert:
|
|
(16.19) |
mit ![]() als frequenzabhängige
Amplitudenverteilung und
als frequenzabhängige
Amplitudenverteilung und ![]() die Frequenzkorrektur
nichtzentrosymmetrischer und zentrosymmetrischer Materie sowie deren Übergang
im nichtlinearen Regime. In Abhängigkeit der Parameter p und q können wir die /
lassen sich die Harmonischen klassifizieren. Mit p = q = 1, d. h.
die Frequenzkorrektur
nichtzentrosymmetrischer und zentrosymmetrischer Materie sowie deren Übergang
im nichtlinearen Regime. In Abhängigkeit der Parameter p und q können wir die /
lassen sich die Harmonischen klassifizieren. Mit p = q = 1, d. h. ![]() erhalten wir die
Grundresonanz oder gewöhnliche Resonanz. Mit q = 1,
erhalten wir die
Grundresonanz oder gewöhnliche Resonanz. Mit q = 1, ![]() = 2, 4, 6, ...,
= 2, 4, 6, ..., ![]() ,
, ![]() (NZS) mit
(NZS) mit ![]() bzw.
bzw. ![]() = 1, 3, 5, ...,
= 1, 3, 5, ..., ![]() ,
, ![]() (ZS), d. h.
(ZS), d. h. ![]() , erhalten wir die harmonische Lösung in p- ter Ordnung, d.
h. die hohen Harmonischen. Mit p = 1 und
, erhalten wir die harmonische Lösung in p- ter Ordnung, d.
h. die hohen Harmonischen. Mit p = 1 und ![]() = 2, 4, 6, ...,
= 2, 4, 6, ..., ![]() ,
, ![]() mit
mit ![]() , d. h.
, d. h. ![]() erhalten wir die
subharmonische Lösung in q- ter Ordnung für Oberflächen bzw.
erhalten wir die
subharmonische Lösung in q- ter Ordnung für Oberflächen bzw. ![]() = 1, 3, 5, ...,
= 1, 3, 5, ..., ![]() ,
, ![]() für Bulk. Wohlgemerkt
definiert am realen Spektrum. Für hohe nichtlineare Näherungen bis zu kleinen
Größen 7. Ordnung lassen sich insgesamt folgende Korrekturfaktoren für erzeugte
hohe Harmonische bestimmen:
für Bulk. Wohlgemerkt
definiert am realen Spektrum. Für hohe nichtlineare Näherungen bis zu kleinen
Größen 7. Ordnung lassen sich insgesamt folgende Korrekturfaktoren für erzeugte
hohe Harmonische bestimmen:
|
|
(10) |
Damit lassen
sich sofort die Frequenzkorrekturen an Oberflächen und Bulkmaterialien
erzeugten hohen Harmonischen bestimmen.
Für
multichromatische Laserexperimente mit z. B. vier Einstrahlungsfrequenzen
erhalten wir:
|
|
(11) |
|
|
(12) |
wobei dies
einer Kombination beider Systeme entspricht:
|
|
(13) |
6. Literatur:
[SYR84] Shen, Y.
R. The Principles of Nonlinear Optics; Wiley: New York, 1984.
[Boyd] Boyd, R.
W. Nonlinear Optics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003.]
[PFTV92] W. H.
Press, B. P. Flannery, S. A. Teukolsky, und W. T. Vetterling, Numerical Recipes in C, 2nd ed., Press Syndicate of the University
of Cambridge, 1992.
Kombination von Theorie
und Praxis: Zum einen werden die numerischen Algorithmen vorgestellt und zum
anderen C- oder Fortran-Programme mitgegeben, die diese Algorithmen
implementieren.
[BSMM08] I. N.
Bronstein, K. A. Semendjajew, G. Musiol, H. Mühlig, Taschenbuch der
Mathematik, 7., vollständig überarbeitete und ergänzte Auflage, Verlag
Harri Deutsch, Frankfurt am Main, (2008)
[LL07- I] L. D. Landau und E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.I: Mechanik, 14., korrigierte Auflage, Akademie-Verlag, Berlin, (2007)
[LL09] L. D. Landau und E. M. Lifschitz, Lehrbuch der Theoretischen Physik,
Bd.II: Klassische Feldtheorie, 12. Auflage, Akademie-Verlag, Berlin, (2009)