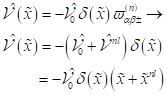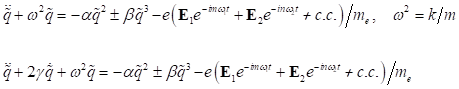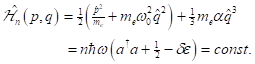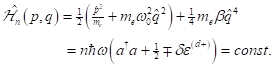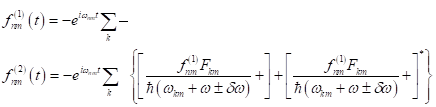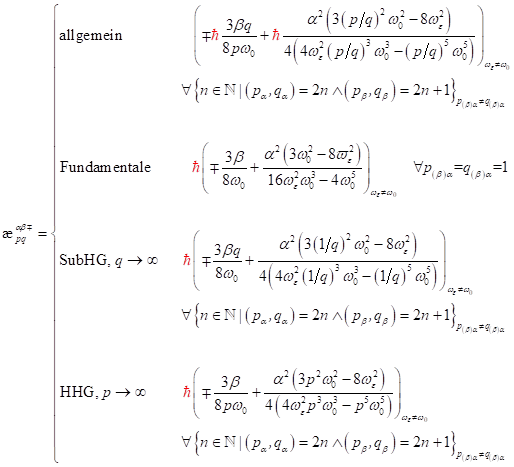Non-linear quantum optics
Peter Krampl*
Chapter 1
Non-linear potential
1.1
Introduction
Photons
can be described with the Maxwell-equations. The wave equation must be used for
electrons. First of all the electron is considered in
the non-linear regime. For that a non-linear potential must be developed. In nichtdissipativer surroundings
the potential can be modelled by means of a non-linear Delta Distribution.
Following potentials submit to dependence of the matter symmetry of the bound
electron:
|
|
(1) |
with
|
|
(2) |
For
the basic state energy is found in
total:
|
|
(3) |
d. h.
this Entspricht the linear case. For higher
approximations surrenders for the stimulated energy corrections states of the
form:
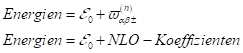
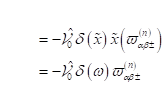
The
formulation of the quantum mechanics based on the description of the density]> operator for
states goes back to new man and Landau, but their application
was restricted only on few states. It is important for the description high
Harmonious
to describe new methods to investigate with the objective
the dynamics with many states or even with a continuous spectrum. Therefore a method is presented in
this section, in which departing from atomic two level can be closed systems on
N level systems. Atomic two state systems can be solved according to the draft from Boyd
(2003) exactly analytically. On basis of this solution strategy an
iterative algorithm to the calculation of multilevel systems
of molecular Suszeptibilitaeten / tensor is presented,
which through Electron- to be induced multiphoton interaction. At first a
mathematical and numeric basic structure of the noncentrosymmetrical
system is elaborated for this purpose in order to describe first of all the
density]>
operator in his chronological development
under dissipativen conditions. The representation of
the density
operator bases on an iterative algorithm with one quartermaster- spectral
method, which a description of his chronological
dynamics in the local room, as well as the behavior in the k- Raum allows. Broadened expressions the "optical
Bloch" Equations can be formulated.
1.2
Non-linear dynamics
The molecular, quantum mechanical description of the
sum frequency production
An unharmonic oscillator
model is developed to the description of the kinetics of measure-afflicted
corpuscles in the non-linear potential. The qm
quantum well represents the potential in the surroundings
of the Gelichgewichtslage. The spatially
restricted delta potential the non-linear correction. In this way differential
equation following in total can be taken as a basis:
|
|
(4) |
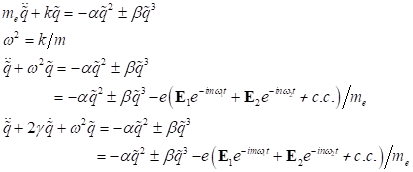
at what the non-linear trailing force of the
oscillators of a
hard,
and/or with
one always soft becoming
characteristic corresponds
|
|
(5) |
In this way the non-linear
oscillator potential to be considered for the measure-afflicted corpuscle in
shape surrenders:
|
|
(6) |
Using
V or U spelling possible V potentially!!!
The Hamilton-operator submits in this way too to
dependence of the matter symmetry taken as a basis:
|
|
(7) |
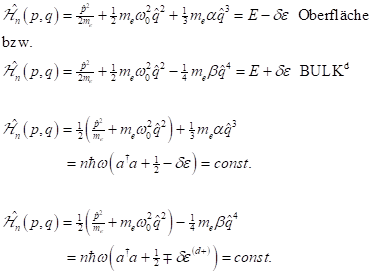
DELTA-potential:
Perturbation
theory:
Solution
loaded unharmonic oscillator in the alternating field
In this way the Hamilton-operator must be reformulated
according to:
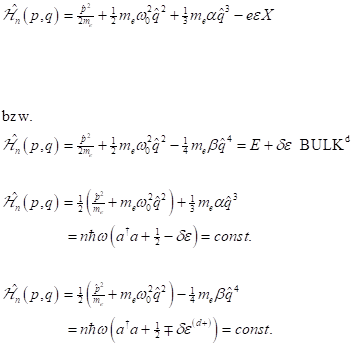
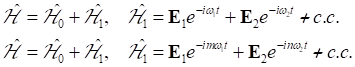
1.3
Construction of non-linear wave
functions
The non-linear wave function becomes in the following
one through combination of the classical quantum well with one delta-
Potentially constructs.
|
|
(8) |
With the underlying energy correction coefficients
universal expressions for the
non-linear coefficients zentro- and noncentrosymmetrical matter above those one interface, in
the approximation of small sizes to 2nd order formulate<A[formulate|word]>
according to:
|
|
(9) |
with the Skewnesskoeffizienten
of the Anharmonizitaet,
, that with
unremunerated and with
positively remunerated Festkoerperbulk
considers.